PROCES DONOŠENJA ODLUKE

UVOD
Svaka odluka predstavlja izbor između najmanje dve alternative (opcije, akcije) pomoću kojih ostvarujemo određene ciljeve.
Na osnovu čega možemo zaključiti da li je odluka koju smo doneli ispravna? Uopšteno govoreći, postoje dva osnovna pristupa:
- ex ante → pre nego što izvršimo izbor detaljno analiziramo i ocenjujemo moguće ishode svake akcije
- ex post → nakon realizacije izabrane akcije merimo njene efekte
Sam proces donošenja odluke podrazumeva, pre svega, analizu našeg trenutnog stanja i precizno definisanje cilja koji želimo da ostvarimo. Nakon toga neophodno je identifikovati sve moguće alternative i evaluirati ih (navodimo prednosti i nedostatke), što predstavlja osnovu za vršenje izbora i donošenje odluke. Na kraju, sprovodimo izabranu alternativu i analiziramo rezultat koji smo postigli.

Prema normativnoj teoriji odlučivanja, donosilac odluka je savršeno racionalan, što znači da uvek i u svakoj situaciji zna šta hoće i vođen je principom maksimizacije lične dobrobiti. Naravno, ovo je samo teorijska pretpostavka koja se navodi radi jednostavnosti analize. U praksi, savršeno racionalan pojedinac ne postoji, iz razloga što često odluke donosimo brzopleto i nepromišljeno, pa čak i na sopstvenu štetu. Osim toga, evaluacija pojedinih alternativa je uglavnom bazirana na subjektivnim kriterijumima (našim željama, interesima, ukusima i slično), tj. takozvanim individualnim preferencijama.
ELEMENTI ODLUKE
- Alternative (opcije, akcije)
- Događaji
- Ishodi

Tumačenje:
Redovi u tabeli predstavljaju moguće akcije (Ai, i=1,2...,m) između kojih vršimo izbor, a kolone događaje (Sj, j=1,2,...,n) u kojima se akcije sprovode. U njihovom preseku nalaze se ishodi akcija (Vij, i=1,2,...,m, j=1,2,...,n). Da bismo na pravilan način kontruisali tabelu odlučivanja, neophodno je da analizom obuhvatimo sve alternative i da događaji međusobno budu isključivi (ne mogu se istovremeno realizovati dva ili više događaja).
DOMINANTNE I DOMINIRANE AKCIJE
Prilikom poređenja akcija, moguće je odrediti tzv. dominantne, odnosno dominirane akcije. Dominantna akcija je ona akcija čiji su ishodi prilikom realizacije bilo kog od navedenih događaja jednako dobri, i u barem jednom od događaja bolji od neke druge akcije. Za dominiranu akciju važi suprotna logika.
Primer: Pretpostavimo da žurimo na posao do kog obično idemo gradskim prevozom, međutim, ulica kroz koju prolazimo zatvorena je zbog građevinskih radova i linije gradskog prevoza kasne. Razmatramo dve moguće akcije (opcije): zaustavljamo taksi ili idemo do posla peške. Imajući u vidu da postoji mogućnost zastoja u saobraćaju, ni vožnja taksijem nam ne garantuje da ćemo na posao stići na vreme. Problem možemo predstaviti sledećom tabelom odlučivanja:
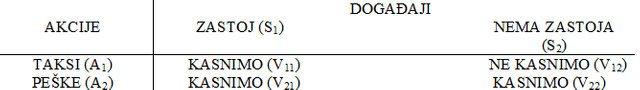
Ukoliko se realizuje događaj S1, ishod obe akcije je isti – kasnimo. Međutim, ukoliko se realizuje S2, biramo A1, jer u tom slučaju stižemo na posao na vreme. Dakle, zaključujemo da je u ovom primeru A1 dominatna akcija, dok je A2 dominirana.
Ipak, postoje i slučajevi kada ne možemo odrediti dominantnu akciju. Ukoliko malo proširimo prethodni primer, dobijamo sledeću tabelu odlučivanja:
Ishodi predstavljaju kašnjenje izraženo u minutima. Vidimo da, ukoliko se odlučimo za A2, svakako kasnimo na posao, ali dužina kašnjenja ne zavisi od zastoja u saobraćaju i, bez obzira na to koji se od tri moguća događaja realizuje, iznosiće 20 minuta. S druge strane, ishod izbora akcije A1 itekako zavisi od toga koji se će događaj realizovati.
Izbor vršimo poređenjem akcija za svaki događaj pojedinačno:
- S1 – biramo A1
- S2 – biramo A1
- S3 – biramo A2
Dakle, u ovom slučaju ne postoji dominantna akcija.
DRVO ODLUČIVANJA
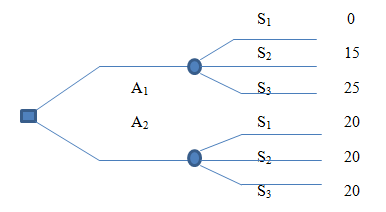
Osim preko tabele odlučivanja, problem donošenja odluke možemo predstaviti i grafičkim putem preko drveta odlučivanja. Konstruiše se s leva na desno i osnovni elementi su:
- čvor odluke – kvadrat
- čvorovi događaja – krugovi
- grane – akcije i događaji
- kraj drveta – ishodi
RELACIJE PREFERENCIJE
Prilikom poređenja bilo koje dve alternative, možemo uspostaviti tri vrste relacije preferencije:
- stroge preferencije (≻) → ukoliko je jedna alternativa nedvosmisleno bolja od druge
- slabe preferencije (≽) → ukoliko je jedna alternativa barem jednako dobra kao druga
- indiferentnost (~) → ukoliko smo jednako zadovoljni i jednom i drugom alternativom
Na osnovu relacija preferencije možemo formirati rang listu alternativa:
A1 ~ A4
A2 ≻ A1
A3 ≻ A4
A2 ≻ A3
A1 ≻ A5

Odlučujemo se za alternativu A2.
Sve tabele su rađene u Word-u.
REFERENCE:
- Pavličić, D. (2018) Teorija odlučivanja
- https://en.wikipedia.org/wiki/Decision_theory
- http://www.dmi.uns.ac.rs/site/dmi/download/master/primenjena_matematika/MilosKnezevic.pdf



Ovo je jako zanimljiva tema i lep uvod u teoriju igara .Uz to bi isao i klasican skolski primer prisoner dilemma, verovatno znas o cemu pricam :D
Nemoj da stajes sa ovim serijalom :)
Hvala ti mnogo! :) Da, da, pisala sam već o tome. :D
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Congratulations @bojana.m95! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Hi @bojana.m95!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV