Scilab Tutorial | Approximating an integral by adding rectangular bands
What Will I Learn?
- You will learn how to make an approximation of the value of an integral by using the Riemann sum concept.
- At the end of this tutorial you will be able to build simple functions and define functions online in Scilab.
What will you need?
- You need to have installed Scilab in your computer. I'm gonna use 5.5.2 version.
- Basic Real Analysis knowledge
- Programming knowlegde.
Difficulty
- Basic
Tutorial Contents
In this tutorial we're gonna write the statements to define a function (a real function) and calculate an approximation of its Riemann integral. You will notice that it will be a very good approximation as long as we provide suitable parameters. Then, we're gonna write an script which will contain a function named
Integrateand it will recieve three parameters (t1,t2,N) and return the approximate value of the integral, in order to you can use it whenever you want. Finally we're gonna check that our approximation actually works by doing an exercise and using thedeffcommand.
I hope to you enjoy it!
Let's begin!
The integral
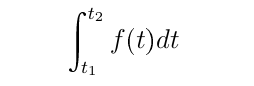
can be approximated by adding rectangular bands whose width is h, as follow:
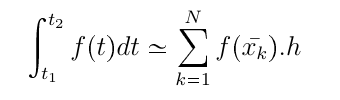
where h is:
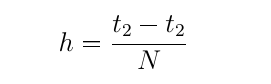
N is the number of bands or rectangles, therefore N determines the quality of the approximation since the more rectangles there are the smaller will be the error. Take a look of the following picture.
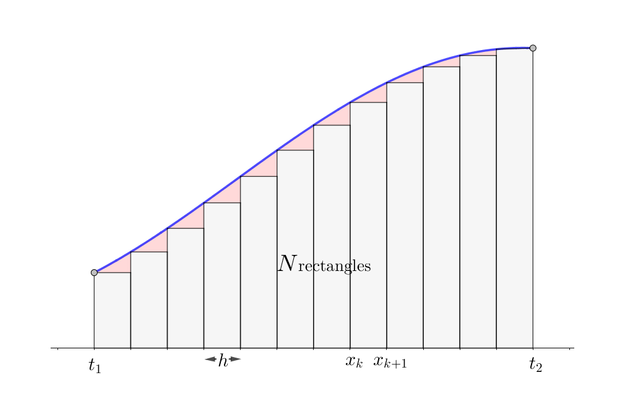
You can consider the red area as the error.
There are many ways for numerical integration. This method consists of adding rectangles in order to approximately calculate the area under a curve.
Code
Let's begin building a Scilab function which will represent a real function. You can define any function you want but no continuous functions.
Step one
Declare a function.
You must provide name, inputs and outputs of the function. We're gonna declare a function called f with x as input and y as output. Of course, you can choose other names.

Step two
Setting the parameters of the integral.
Set the number of bands by giving a value for N. Remember that the higher is N the more exact will be the result. h is the width of each rectangle. Then, set up variable xk as height of the first rectangle. We're also going to initialize variable area as the area of the first rectangle.

Step three
Finally, we 're gonna calculate the sum of all rectangle areas using a for cycle. area will store the whole calcuted area after each cycle. The number of cycles is N-1 due to we had already calculated the first rectangle area in the previous step.

The complete code with N=100.
function[y]=f(x) //name: f, y:output, x: input
y=sin(x); //Body: f(x)=sin(x)
endfunction
//Let's calculate integral of sin(x) from 0 to %pi
// Limits of integration
t1=0;
t2=%pi;
//
N=100; //Number of bands
h=(t2-t1)/N; //Rectangles width
xk=t1; //Height of first rectangle
area=f(xk)*h; //Area of first rectangle
//summation of f(xi)*h
for k=2:N
xk=xk+h;
area= area+f(xk)*h;
end
disp(area,"area="); //Show the result
The aproximated area using 100 bands.

deff command
Now let's write an script which contains a function called Integrate so that we can use this function anytime.
Step one
Crate a new file in SciNotes and call it as you wish. Then, define a function, as we did in the previous section. This function will have three inputs: t1,t2,N , th limits of integration and the number of bands, and one output: result, the final result.
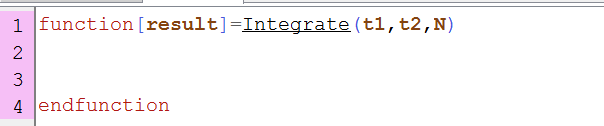
step two
The body of the function is the same algorithm we used in the previous section.
The final code is shown below:
function[result]=Integrate(t1,t2,N)
h=(t2-t1)/N
xk=t1
result=f(xk)*h
for k=2:N
xk=xk+h
result=result+f(xk)*h
end
endfunction
Execute this code before go to the next step.
Step three
In this step let's introduce the *deff command.
deff command allow us to define a function in a online way. Take a look of its syntax:
deff('[s1, s2, ...] = newfunction(e1, e2, ...)',text [,opt])
S1, S2,... are outputs and e1,e2,... are inputs. For example we can write the statement
deff('[f1, f2]= functionname(x,y)', ['f1=x^2+y^2'; 'f2=y'])
and define a function from sequences of instructions written in text strings. This function will have the same properties than functions we have already created.
We're gonna use deff to define a real function called f.
Step four
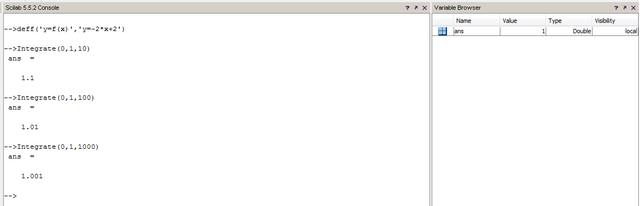
Now let's go to the console to define a function there with deff command. Take care about call it f since we called f to the function within Integrate. Once you have defined your real function, you can try the Integrate function.
This is it for now. I hope you've learned something new.
Thank you for reading!
Curriculum
Posted on Utopian.io - Rewarding Open Source Contributors
Am lucky to have come across you. I have problem with mathematic , I hope to learn from visiting your site
Glad to have you over here!
Best
Thank you for the contribution. It has been approved.
You can contact us on Discord.
[utopian-moderator]
Thank you! @cha0s0000.
Hey @miguelangel2801 I am @utopian-io. I have just upvoted you!
Achievements
Suggestions
Get Noticed!
Community-Driven Witness!
I am the first and only Steem Community-Driven Witness. Participate on Discord. Lets GROW TOGETHER!
Up-vote this comment to grow my power and help Open Source contributions like this one. Want to chat? Join me on Discord https://discord.gg/Pc8HG9x
Nice math!