What is the Ethereum Metropolis: The Ultimate Guide
(1) What are the four stages of Ethereum in "Metropolis"
This is not the first time Ethereum has upgraded, and it will not be the last. Ethereum is not only designed as a currency model, but also a decentralized application platform. Before finally reaching this goal, it needs to go through different growth stages. In each stage, Ethereum will introduce different features to make the system more stable and powerful.
The complete development path of Ethereum is divided into four stages, namely "Frontier" (Frontier), "Homestead" (Homestead), "Metropolis" (Metropolis) and "Serenity" (Serenity). "Metropolis" is the third of the four stages of Ethereum's development. With its arrival, Ethereum will add many interesting features. Here are some features that will have a significant impact on Ethereum, namely:
(2) Four characteristics of "Metropolis"
Feature 1: zk-SNARKs
The biggest and most important feature of "Metropolis" is the implementation of zk-SNARKs. The full name of zk-SNARKs is Zero-Knowledge Succinct Non-Interactive Argument of Knowledge, that is, "concise non-interactive zero-knowledge proof." zk-SNARKs are based on "zero knowledge proof" (ZKP).
What is "zero-knowledge proof"?
"Zero knowledge proof" was proposed by S. Goldwasser, S. Micali and C. Rackoff in the early 1980s. It refers to the ability of the prover to convince the verifier that a certain assertion is correct without providing any useful information to the verifier. "Zero knowledge proof" is essentially an agreement involving two or more parties, that is, a series of steps that two or more parties need to take to complete a task. The prover proves to the verifier and makes it believe that he knows or possesses a certain message, but the certification process cannot leak any information about the certified message to the verifier. A lot of facts prove that "zero-knowledge proof" is very useful in cryptography. If "zero-knowledge proof" can be used for verification, many problems can be effectively solved.
"Zero-knowledge proof" can be established must have the following three elements:
Completeness: If the statement is true, then an honest verifier can be trusted by an honest prover;
Reliability: If the statement is false, it is not ruled out that there is a certain probability that the deceiver can convince the honest verifier that it is true;
Zero knowledge: if the statement is true, then the verifier does not know any information about the statement during the certification process;
"Zero-knowledge proof" is not proof in the mathematical sense, because it has a small probability of error, and the deceiver may deceive the prover through false statements. In other words, "zero-knowledge proof" is a probabilistic proof rather than a deterministic proof. But there are also technologies that can reduce the error to a negligible value.
The formal definition of zero-knowledge must use some calculation models, the most common is the calculation model of Turing machine.
Here are two examples to illustrate zero-knowledge proof:
- Suppose there is a room that can only be opened with a key and cannot be opened by any other methods. Alice wants to prove to Bob that she has the key to this room. At this time, there are two ways:
① Alice shows the key to Bob, and Bob uses the key to open the lock of the room, thus proving that Alice has the correct key for the room
② Bob determines that there is an object in the room, and Alice uses the key she has to open the door of the room, and then takes out the object and shows it to Bob, thus proving that she really has the key to the room
The latter ② method is a zero-knowledge proof. The advantage is that in the entire certification process, Bob can never see the key, thus avoiding the key leakage.
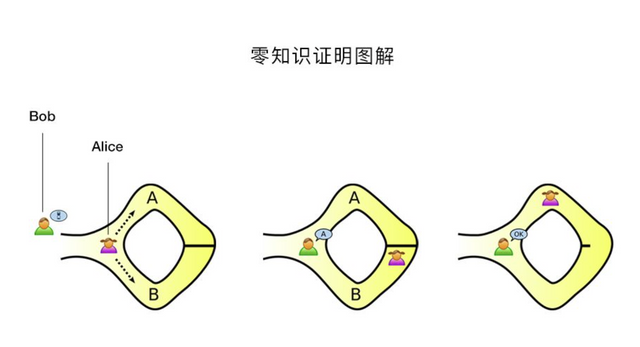
- This is a very classic example: there is a gaped circular corridor, the exit and entrance are very close (within eye distance), but somewhere in the middle of the corridor there is a door that can only be opened with a key. Alice wants to Bob proves that he has the key to the door. With zero-knowledge proof, Bob watches Alice enter the corridor from the entrance, and then walks out of the corridor from the exit. At this time, Bob doesn't get any information about the key, but he can prove that Alice owns the key.
The above two examples are the "operation" of zero-knowledge proof in the real world, so how do we realize the application of zero-knowledge proof in the blockchain through zk-SNARKs?
How does zk-SNARKs work?
zk-SNARKs is composed of 3 algorithms: G, P, V.
G is a key generator, which needs to generate random variable L (must ensure that it cannot be leaked under any circumstances) and program C. Then generate two public keys-the certification public key Pk and the verification public key Vk. Both of these public keys are public and anyone can view them.
P is the prover, and three parameters need to be input, namely, the proof public key Pk, the public random input hash value x, and the privacy statement w that needs to be proved. P algorithm generates proof prf, the function is expressed as: prf = P (Pk, x, w)
As the verifier, V will return a Boolean result, which is true or false. V verifies the public key Vk, the random input hash value x in P, and the proof prf as input parameters, that is, V (Vk, x, prf). If the prover is correct, return true, otherwise return false.
From the relationship between G, P and V above, it can be seen that the random variable L is very important and must be kept secret. Because anyone can use it to generate false proofs, these false proofs can also return true, regardless of whether the prover has knowledge of the privacy statement w.
Let us continue to return to our old friends Alice and Bob. Alice is the prover and Bob is the verifier.
The first thing Bob, as a verifier, is to use G to generate the proof public key Pk and the verification public key Vk. For this purpose, he needs to generate a random variable L. As mentioned above, Bob must be very careful with L. He cannot let Alice know The value of L in case Alice creates a false proof.
Now that Bob has generated two public keys, Alice needs to generate a proof prf to prove the validity of the statement. She will use the proof algorithm P to generate a proof to prove that she knows that the hash value of the privacy statement w is x. Next, Alice will pass these proof parameters to Bob who finally runs the zk-SNARKs verification algorithm. Bob will use the verification algorithm V (Vk, x, prf) to verify the result. If it returns true, then Alice is sincere and really knows what the privacy statement w is. If it returns false, then Alice is lying and she knows what w is.
https://www.samajwadipartynews.in/2022/06/What-is-meant-by-samajwadi-party-system-know-briefly.html