Initial thoughts about Information Theory
(cross-posted from my SubStack)
Initial thoughts about Information Theory
Some ideas I found interesting while watching the “Science of Information” course
Last week, one of the “free this week” options on my cable provider was The Great Courses. I’ve been meaning to learn more about Information Theory because I have suspected it would be useful for several of the ideas I’ve been pondering lately, but haven’t wanted to shell out money for a textbook treatment of the subject. So even though I didn’t really know much about the quality of the courses I checked through the offerings and noticed one called The Science of Information: From Language to Black Holes and thought I would try it. While some of the applied ideas were already familiar to me from some electrical engineering classes I took back in college, I found the course very interesting. It didn’t go deep into the technical details but was more a broad overview, weaving in stories about the history of the field with interesting examples of how it’s relevant to a wide variety of applications. The groundbreaking work of Claude Shannon, who developed the ideas in the 1940s while working with radio and telephone communications, is the root and narrative throughline of the course, and it continues up through the present and possible future with talk about quantum computing and quantum information theory.
What is Information?
To develop the original concepts Claude Shannon made the simplifying assumption that he wasn’t interested in exploring the meaning of messages[1], just the ability to distinguish among the possible messages that a sender could send through a communication channel to a receiver. An intuitive basic piece of information is the answer to a Yes/No question, a bit, so bits are the unit used to quantify information. For a variety of good reasons it makes sense to use a logarithmic measure of the number of options, which maps to the number of bits you’d need to enumerate the choices in binary – if you can send A, B, C, D, E, F, G, or H, i.e. 8 possible options, that’s log₂(8) = 3 bits.
He then incorporates the idea of surprise. Even though a fire alarm is a 1-bit signal (either “no fire” or “fire!”) it intuitively feels like you get a lot more information from the rare “fire!” message than from the common stream of quiet “no fire, no fire, no fire” messages, so he defines surprise by the inverse of the probability of getting a particular message, 1/p(x), and incorporates that into a formula for what is usually called Shannon Entropy, a measure of information, as the average log surprise:
H = Σ p(x)*log₂(1/p(x))
He called this entropy by either analogy or due to the similarity to some entropy equations from physics, but there’s a more modern understanding of entropy that looks at them as being the same thing.
Information Channels
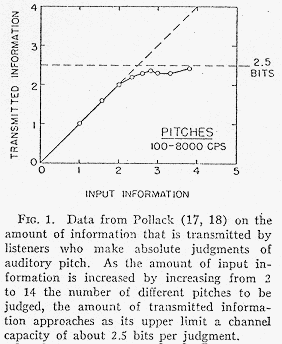
This approach had a lot of useful applications for things like data compression, error correction, thinking about signal relative to noise, and other fields. For example, psychologists studying human perception found that the ability to distinguish between single-dimensional differences for a lot of things (pitch, loudness, position of a dot on a horizontal line, the saltiness of water, etc.) seems to work like a communication channel with a capacity of between 2 and 3 bits, as documented in the widely-cited psychology paper The Magical Number Seven, Plus or Minus Two. Most of us are pretty good at telling the difference between stimuli when there are that many choices or less, but if there are more options in the range we start making mistakes.
Physics Entropy as Shannon Entropy
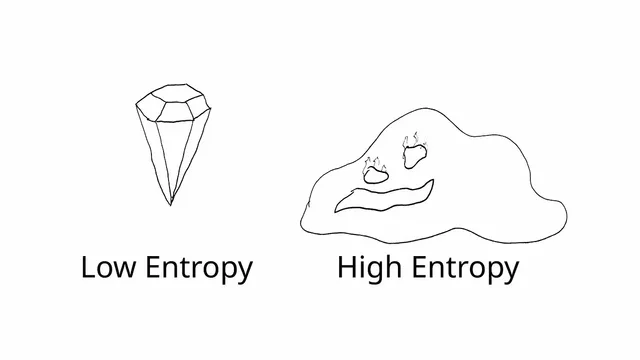
I had vaguely known that there was a relationship between Information Theory and the entropy from thermodynamics (this is one of the reasons I was interested in learning more about it), but the most compelling thing I learned in the course was that my intuition had things backwards. An example of something with low entropy is something cool and orderly, like a crystal. And an example of something with high entropy is something disorderly and chaotic, like a blob of lava.
My intuition, maybe influenced by the way we often see crystals used in fantasy and sci-fi, was to think that the orderly crystal has a lot of information while the chaotic blob has little, but this is exactly backwards! The problem is that putting a label like “random” on it was leading me to think of all the parts of the blob as the same, but in reality every part of them is different so there is a lot of information you don’t have about the blob! Whereas with the crystal, since it’s so regular and repeating, there’s less information required to know about the whole thing. Regular, orderly, low-entropy things have less information per unit than high entropy things! Realizing this helped the “information” view of entropy click into place for me (and also served as a reminder about how labels and shorthands, while sometimes helpful, shouldn’t be mistaken for the real thing).
![]()
(This image is quite different from one that has the same medium gray in every pixel)
The Quantum Realm
I had to cram the later lectures a bit in order to get the whole thing finished while it was still free, so I’m sure I didn’t absorb everything from the quantum section of the course, but one thing I found really interesting was about a thought experiment related to the maximum amount of information you could store in a given volume. They realized that adding information also involved adding energy, but if you add enough energy to a fixed space you would cross a threshold where it becomes a black hole (which is interesting from an information perspective because of the “nothing comes out of them” feature of black holes – is the information lost?). Apparently the math works out such that it’s the surface area of a region rather than the volume that limits the amount of information that you can put somewhere. I’m not sure of all the implications yet, but I find the idea of a relationship between surface area and information to be really intriguing.
Closing Thoughts
While this post wasn’t directly about games, game design, RPG Theory, etc., part of my motivation for learning about Information Theory was because I’ve been intrigued about the idea of entropy as the thing that makes certain processes proceed in one direction but not the other, and whether there are analogies for game design about what makes a game feel like it’s “moving forward”. I’m also wondering if there may be some analogies to other things, e.g. why “reacting” seems to flow more easily than “initiating”. Also, the notion of “exploration” as the basic activity of a roleplaying game seems to directly be about information. After seeing some of the Information Theory approaches to cryptography in the course I wonder if it might be useful form of analysis to think in terms of what you do or don’t know (about the game, about yourself, etc.) that you gain information about through the moment-by-moment interactions of play. The stuff about the 2-3 bit resolution of sensory information seems like it might be relevant to the design of RPG stats, and I wonder if things that work like quantities but don’t have measurable real-world correlates have similar effects (e.g. emotional intensity, the feeling of how “complex” something is, how bad a moral violation is, the “power level” of a superhero, etc.), and what that might mean for game design. In a lot of ways I’ve been feeling more inspired by watching this course than any of the other nonfiction content I’ve consumed lately.
[1] One reason for this is that the sender and receive can be communicating in code, presumably transmitting “the eagle flies at midnight” is communicating something even if we don’t know what that is.