Función de producción Cobb-Douglas
Es una función de la teoría neoclásica en donde se proyecta el crecimiento económico de un país y su producción, representando en ella la relación que tiene la tecnología, capital y el trabajo. Fue evidenciada por los economistas Charles Cobb, y Paul Douglas en el año 1928, de ellos deriva su nombre.
Se representa así:
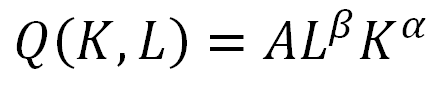
En donde:
- Q: es la cantidad de producción
- L: es la cantidad de trabajo (normalmente medido en horas-hombre)
- K: es la cantidad de capital empleado
- A: representa el nivel de tecnología dado
- α y β: representan el nivel de elasticidad de los factores productivos, ambos son positivos y son menores a 1
Esta función fue creada debido a un estudio que se hizo en E.E.U.U sobre la distribución de la renta entre el capital y el trabajo, se observó que la producción se mantenía constante al pasar de los años, es decir que la producción aumenta paralelamente con el trabajo y el capital. Ejemplo, si aumento la combinación de mis factores productivos en un 20 %, mi producción aumentará en un 20 %.
Cobb-Douglas tiene distintas aplicaciones tales como:
Productividad Marginal
La productividad marginal es el cambio en la producción cuando añado un factor adicional manteniendo lo demás constante. Para obtener el producto marginal de un factor, derivamos parcialmente el producto total de la producción respecto al factor de producción en cuestión. Utilizando la función de Cobb-Douglas tenemos que:
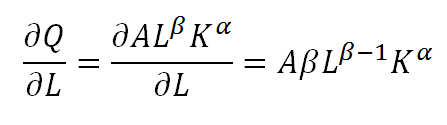
Como β es positivo y menor que 1, esta función será positiva y decreciente. Todos los elementos son positivos, entonces a medida que aumenta el trabajo, aumenta la producción. Pero como β es menor que uno y en la función nueva es negativo (β-1) el trabajo rendirá cada vez menos. Un claro ejemplo de la ley de rendimiento marginales decrecientes.
Gráficamente se observa así:
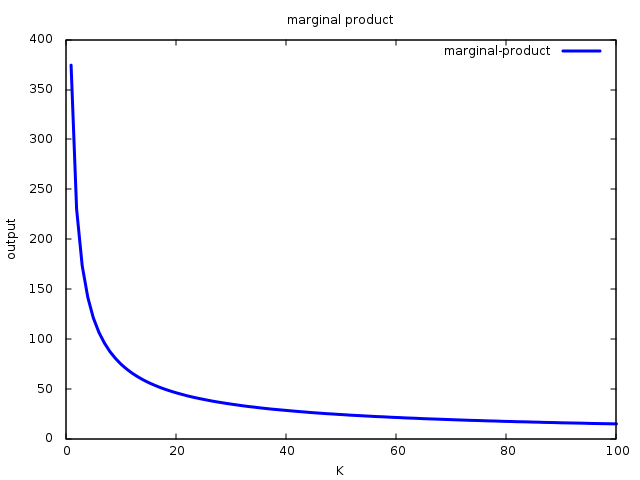
Fuente
Mientras que la producción crece:
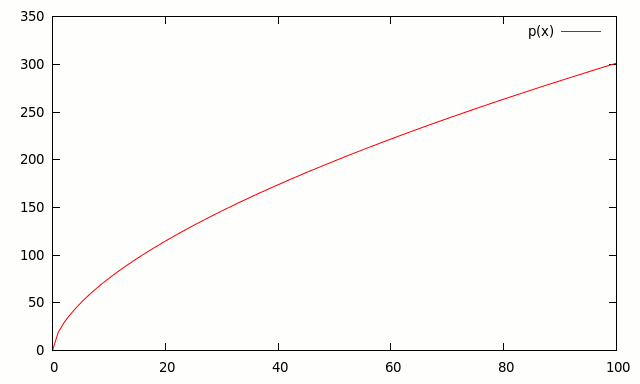
Fuente
Elasticidad de la producción constante
La ecuación Cobb-Douglas es homogénea, su elasticidad es igual a 1, y es constante. La elasticidad mide la variación porcentual de la producción ante cambios de la cantidad de insumos utilizados.
Se denota:
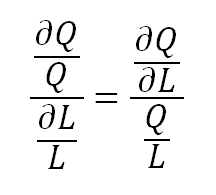
Esta sería la variación porcentual del producto total entre la variación porcentual del trabajo, para así obtener la elasticidad del trabajo.
En la caso de Cobb-Douglas:
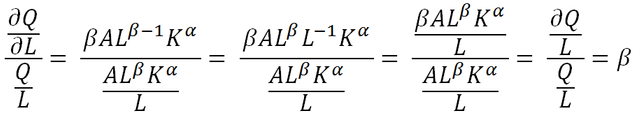
Así se demuestra la elasticidad del trabajo (β), y se puede aplicar también de manera parecida para la elasticidad del capital (α).
Rendimientos a escala constantes
Los rendimientos a escala miden la variación de la producción en función de las diferentes combinaciones de capital y trabajo. Este depende de la suma de α+β. Para calcular los rendimientos a escala de Cobb-Douglas añadimos una constante λ que mide la variación de los insumos.
Ejemplo:
Ante un cambio de λ en la cantidad de factores utilizados, la producción se incrementa en λ^(β+α).
Entonces si:
(β+α) = 1 ; la función de producción tendrá rendimientos a escala constantes
(β+α) > 1 ; la función de producción tendrá rendimientos a escala crecientes
(β+α) < 1; la función de producción tendrá rendimientos a escala decrecientes
Cobb-Douglas es la ecuación de la una gráfica normal de isocuantas, son curvas que miden la diferentes combinaciones de factores productivos para un determinado nivel de producción, son convexas al origen y decrecientes.
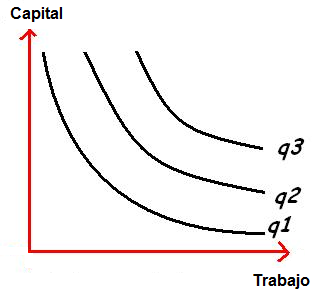
Fuente
En resumen tenemos que Cobb-Douglas:
- Demuestra un producto marginal positivo y decreciente
- Demuestra una elasticidad de producción constante
- Los rendimientos a escala son constantes
- Demuestra Ley de rendimientos marginales decrecientes
Fotos de ecuaciones son mi autoría
Bibliografía:
- https://www.zonaeconomica.com/funcion-de-produccion/cobb-douglas (Consultado el 11 de Mar de 2018)
- https://www.econowiki.com/es/funcion-de-produccion-cobb-douglas (Consultado el 11 Mar de 2018)
- Teoría microeconómica. Principios básicos y ampliaciones. 9a. ed. Walter Nicholson (Página 183 hasta página 198)
- http://www.enciclopediafinanciera.com/definicion-isocuantas.html (Consultado el 11 de Mar de 2018)
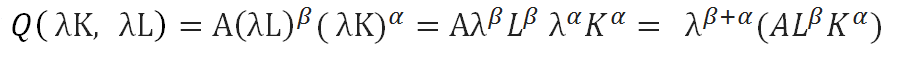
Excelente aporte Fidmary.
¡Gracias Angel!
Muy educativo tu artículo. Gracias por promover la ciencia económica