Deducción de la fórmula de la ecuación de segundo grado
Saludos a la gran comunidad de steemit en español, hace algo de tiempo que estaba inactivo en la página, regrese escribiendo un pequeño artículo sobre estadísticas deportivas pero hoy vengo con un trabajo en mi área y que tiene que ver con la enseñanza de las ciencias en este caso la matemática. En este post muestro la obtención de una fórmula matemática la cual hemos usado muchas veces no solo para resolver problemas algebraicos sino también el ingeniería y en física .
Este artículo es la versión en español del que hice en ingles y que les dejo le link por si gustan verlo (https://steemit.com/steemiteducation/@zambranoacosta/deduction-of-the-formula-of-qudratic-equation) pero en esta ocasión, a parte de reescribirlo en español, le voy a agregar una cosa que vi y me pareció pertinente agregar cuando revisé el texto en el cual me basé para escribir este artículo.
Muy bien sin más que agregar a esta pequeña introducción comencemos.

Figura 1: Fórmula de la resolvente de la ecuación de segundo grado. Imagen tomada de: https://www.dominatethegmat.com/2011/07/quadratic-equations-shortcut-gmat-data-sufficiency/ y editada por @zambranoacosta usando Microsoft paint.
Comenzamos escribiendo la ecuación cuadrática en forma general:
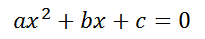
Donde los coeficientes a, b y c son números reales. El coeficiente a debe cumplir con la condición de que sea diferente de cero, ya que si ésta fuese igual a cero, la parte cuadrática desaparecería y sólo quedaría la parte lineal (bx) o una constante (c, si b = 0), b es el coeficiente de la parte lineal de la ecuación y si puede valer cero, c se conoce como término independiente (no depende de x o de la variable independiente con la que e esté trabajando) y también puede llegar a ser nula. Cuándo la función cuadrática se iguala a cero, esto se hace con el fin de hallar los cortes de la función (o de la gráfica de la función mejor dicho) con el eje horizontal donde se ubique la variable independiente, por lo tanto, cuando la ecuación de segundo grado se resuelve, se dice que encontramos los puntos de corte con el eje x o de la variable independiente, a esto también se le dice hallar las raíces de la función.
Ahora, la ecuación cuadrática la multiplicamos toda por 4, recordando que en el lado derecho de la igualdad tenemos un cero, por lo cual 4 x 0 = 0, se tiene:
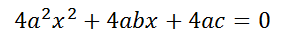
El siguiente paso será sumar en ambos lados de la igualdad el número b^2:

A continuación, movemos el término 4ac del lado izquierdo de la igualdad hacia el derecho:
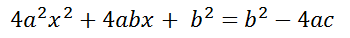
Si observamos el lado izquierdo, vemos que hay desarrollado un producto notable, si extraemos la raíz cuadrada del primer y tercer término y además vemos que el segundo término es exactamente el doble producto de dichas raíces:
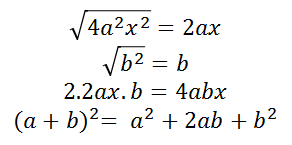
Por consiguiente, la última igualdad puede escribirse como sigue:
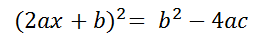
Extrayendo la raíz cuadrada en ambos lados y recordando que, la raíz cuadrada tendrá dos soluciones (una precedida por un + y la otra por un -) se llega a:
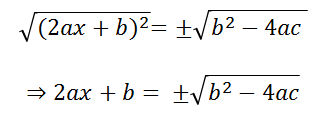
Finalmente al despejar x (pasando b que está positivo en el lado izquierdo de la igualdad a negativo en el lado derecho y 2a que está multiplicando a x, pasará al lado derecho dividiendo) nos queda la conocida fórmula:
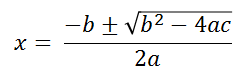
En el resultado final tenemos la fórmula escrita de manera condensada (representado por el símbolo ± delante de la raíz, pero también podemos escribirla, separando las soluciones o raíces de la siguiente forma:
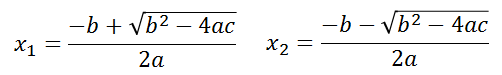
Hasta aquí ya se tiene deducida la fórmula de la resolvente de la ecuación de segundo grado, ahora se hará un análisis de las soluciones de acuerdo a lo que dice la fórmula y también se verificará lo que sucede, en términos de la resolvente, lo que puede ocurrir con algunas variantes de la ecuación cuadrática.
Primero, se analizarán las soluciones a partir de lo que ocurre dentro de la raíz cuadrada de la fórmula, ya que al ser raíz cuadrada, hay que tener cuidado con lo que allí resulte.
La cantidad que se encuentra dentro de la raíz recibe el nombre de discriminante, se representa con la letra griega delta (Δ) y puede presentar 3 variantes:
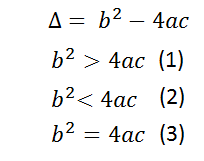
Si se cumple la variante (1), se tendrán entonces 2 soluciones, raíces o cortes con el eje x reales y diferentes, ya que el discriminante en este caso es positivo.
Si se cumple la variante (2), el discriminante dará negativo, por lo cual se tendrá la raíz cuadrada de un número negativo y esto conduce a tener una cantidad imaginaria o un número complejo. Sin embargo geométricamente este resultado tiene sentido ya que muestra que la gráfica de la función no toca al eje x o eje de la variable independiente.
Si se cumple con la variante (3), entonces solo se tendrá una sola solución, pues en este caso, el discriminante daría igual a cero, y la raíz cuadrada de cero es cero, solo quedaría: x = - b/2a y este valor representará un máximo o un mínimo como se comprobará más adelante.
La figura 2 muestra la gráfica de la función cuadrática para los tres casos descritos del discriminante.
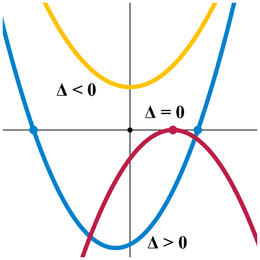
Figura 2: gráfico de la función cuadrática para los tres casos del discriminante discutidos arriba. Imagen tomada de https://es.wikipedia.org/wiki/Ecuaci%C3%B3n_de_segundo_grado
Para comprobar lo que se dijo de la tercera variante, es decir, probar que el resultado de una sola raíz x = - b/2a es un máximo o un mínimo (o punto crítico) aplicaremos el criterio de la primera derivada, es decir, se tomará la derivada de la función cuadrática, se igualará a cero y se resolverá la ecuación dada para x:
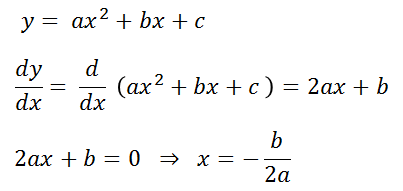
Es decir, el criterio de la primera derivada, el cual se usa para encontrar puntos críticos (puntos donde la gráfica de la función cambia de concavidad o llega a un máximo o mínimo) muestra que la raíz única en el caso dado en la tercera variante del discriminante en efecto es un punto crítico y este punto crítico se denomina vértice de la parábola y al ser un punto del espacio cartesiano x-y, tendrá una coordenada x la cual puede hallarse aplicando x = - b/2a. La coordenada y se halla, sustituyendo el valor calculado de la coordenada x en la función cuadrática.
Ahora se analizarán algunas variantes pero de la función cuadrática, en términos de la resolvente:
En primer lugar, se analizará el caso cuando el coeficiente b = 0. En este caso la ecuación queda:
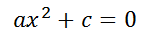
Y la fórmula se escribiría así:
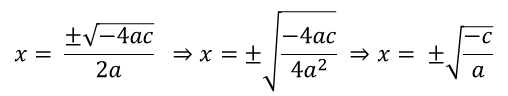
Este resultado establece que si el coeficiente de la parte cuadrática a es positivo, nos quedaría la raíz cuadrada de un número negativo y en este caso, así como en la variante (2) del discriminante, se tendrá una cantidad imaginaria o un número complejo indicándonos que la parábola no tocará el eje de la variable independiente.
Si por el contrario, el coeficiente a es negativo, se tendrán dos raíces iguales y reales, dadas por:
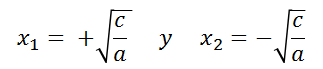
Ahora bien, si el caso es que el término independiente c = 0, la ecuación cuadrática sería ahora:
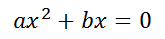
Y la resolvente ahora sería:
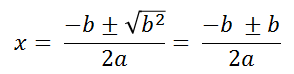
Y al separar las dos raíces:
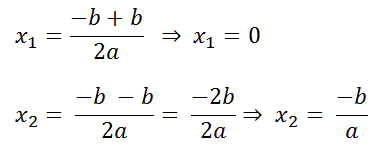
Lo cual significa que uno de los cortes con el eje de la variable independiente será exactamente el origen (0, 0) y el otro punto de corte será x = -b/a y esta cantidad será positiva o negativa dependiendo del signo del coeficiente a.
Con esto damos por concluido este post, espero que el mismo haya sido de su agrado, también espero que se haya asimilado bien ya que lo hice lo más simple posible con el fin de que se pueda entender claramente de donde viene la fórmula de la resolvente de la ecuación de segundo grado así como el análisis de la misma con las distintas variantes que se puedan presentar.
Estoy a la orden para responder cualquier comentario o pregunta que se tenga sobre el tema y si les ha gustado y se le da el suficiente apoyo por la comunidad de steemit, estaré realizando otra sobre los pasos (sistemáticos) para elaborar la gráfica de la función de segundo grado, muchas gracias por leer el artículo y por los votos que este reciba, hasta la próxima.
Saludos cordiales.
Referencias: Álgebra elemental; Aurelio Baldor.
https://www.dominatethegmat.com/2011/07/quadratic-equations-shortcut-gmat-data-sufficiency/
https://es.wikipedia.org/wiki/Ecuaci%C3%B3n_de_segundo_grado