Importancia de la estadística en la producción animal
La mayoría de las personas se imaginan que llevar una finca o una agropecuaria es algo meramente campestre, que no lleva un sentido fuerte de la ciencia y es algo que generalmente poseen personas sin el mínimo conocimiento, por tanto la mayoría de los productores cometen muchos errores básicos y no logran desarrollar el máximo potencial del hato en el que trabajan.
Un punto importante a tratar en cualquier área de la producción animal es la tenencia de cierta capacidad predictiva. Al decir predictiva nos referimos a saber la ocurrencia de un hecho antes de que suceda. Ahora se preguntaran ¿Cómo es posible predecir si mis animales llegarán al peso deseado al momento del destete, si mis animales tendrán altos niveles de fertilidad, que mis pastos lograran sobrevivir a una temporada de sequía, etc.
Estadísticamente tenemos varias opciones por donde podemos trabajar, pero lo mejor será empezar con una breve explicación de conceptos básicos necesarios para entender la manera de predecir cualquier evento.
¿Qué es la estadística?
La estadística es una ciencia que se encarga de estudiar las variaciones de un fenómeno que está sometido a eventos aleatorios, estudia poblaciones y muestras, recolecta, elabora, analiza e interpreta información.
En el caso de la producción animal, las variaciones que estudia la estadística son del tipo biológicas asociadas a las especies animales y vegetales que hacen de objeto de estudio.
¿Qué es una variable?
Se entiende como variable cualquier característica que puede tomar un valor en el curso del proceso de análisis estadístico.
Las variables pueden ser de dos tipos:
Variables cualitativas:
describen los atributos o cualidades de rasgos, son variables que no pueden tomar un valor numérico, por lo tanto no se pueden medir numéricamente, pero si se pueden describir.Variables cuantitativas:
Tienen valores numéricos y por ende se pueden medir. Son ejemplos de este tipo de variables el peso, la edad producción de carne, producción de semen por eyaculado, número de montas, tamaño y la cantidad de pasto que come al día un toro Cebú como el que se muestra en la Fig. 3.Las variables cuantitativas a su vez pueden clasificarse en función del tipo de valor numérico que puedan adoptar, esto es, pueden clasificarse en variables discretas y variables continuas.
Variables discretas:
Son variables que solo pueden adoptar valores enteros. Un ejemplo de este tipo de variables es la puesta de huevos que puede colocar una gallina: Esta puede poner 5 huevos en una puesta, pero no es posible que llegue a tener 5,5 huevos ya que esto sería ilógico; en ningún caso una gallina puede colocar medio huevo o alguna fracción de un huevo, solo valores enteros.Variables Continuas:
Pueden tomar cualquier valor real dentro de un intervalo. El peso de un gallo de 1,4Kg es un ejemplo de una variable continua debido a que este puede tomar además de valores enteros, valores decimales.
La estadística es perfecta para estudiar variables tanto cualitativas como cuantitativas y nos ayuda a comprender como se dispersan, organizan y actúan en el proceso de producción animal. Ya que la estadística estudia una población de interés para el veterinario o ingeniero de producción animal se debe tener claro que significan los conceptos de individuo, de población y de muestra:
Individuo:
Un individo es cualquier elemento que porte información sobre el fenómeno que se estudia. Así, si se estudia el peso de cada toro cebú que habita en una finca, cada toro es un individuo.Población:
Conjunto de elementos con alguna característica de interés para el investigador y que debe estar delimitada por el espacio y el tiempo. Generalmente no se trabaja con toda la población ya que para el investigador sería más trabajo y gastos así que se trabaja con una muestra o parte de la población.Muestra:
Subconjunto de la población estudiada tomada para estudiar las características de la misma, debe ser representativa y debe tener un tamaño adecuado.En la estadística se reduce, es decir se estiman o toman valores representativos de la población o de la muestra y son usados como referencia para realizar cálculos a través de diversos modelos. Uno de los modelos mas usados es el de las medidas de tendencia central
Medidas de tendencia central:
son medidas estadísticas que pretenden resumir en un solo valor a un conjunto de valores. Representan un centro en torno al cual se encuentra ubicado el conjunto de los datos (Media, Moda y Mediana).
Media:
Es el valor característico de una serie de datos cuantitativos, objeto de estudio que parte del principio de la esperanza matemática o valor esperado de un grupo datos de tamaño n y que pueden tomar el valor Xi .
Moda:
Es el valor que más se repite en una muestra.
Mediana:
Representa el valor de la variable de posición central en un conjunto de datos ordenados.
Orden medianal:
Indica en qué posición esta la mediana en datos ordenados. De no estar ordenados se deben ordenar de menor a mayor.
Para mayor claridad, se mostrara un ejemplo de la aplicación de estos conceptos en veterinaria.
Se pide la MODA, MEDIANA Y MEDIA de la producción de leche de 15 vacas mestizas cebú del distrito torre del estado Lara.
11-10-8-15-22-11-16-17-14-5-12-11-8-13-10 (Litros de leche por día)

Conclusiones Generales:
- Los animales como promedio general producen 12, 2 litros de leche (Es una información general que puede usar el productor para saber el nivel de producción de su rebaño).
- El 50% de sus animales producen menos de 11 litros (Es una información que puede usar el productor para destacar el punto medio de su producción).
- La mayoría de los animales producen 11 litros (Es una información que puede usar el productor para saber cuál es su nivel de producción más frecuente).
Medidas de dispersión:
Son parámetros estadísticos que indican cómo se alejan los datos respecto de la media aritmética. Sirven como indicador de la variabilidad de los datos (Varianza, Desviación Estándar, Rango y Coeficiente de variación).
Rango:
Indica la dispersión entre los valores extremos de una variable. Se calcula como la diferencia entre el mayor y el menor valor de la variable:
Varianza:
Es una medida de dispersión definida como la esperanza del cuadrado de la desviación de dicha variable respecto a su media:
Desviación Estándar:
Se define como la raíz cuadrada de la varianza (Se calcula porque la varianza solo da resultados al cuadrado y eso lleva a la confusión del investigador, al sacarle la raíz a la varianza se elimina el cuadrado):
Coeficiente de variación:
El coeficiente de variación es la relación entre la desviación típica de una muestra y su media.
Ilustremos los conceptos anteriormente dados con un ejemplo:
Calcular el Rango, la varianza, la desviación estándar y el coeficiente de variación de la producción de leche de cinco cabras.
Produccion de leche: 2,3,6,8,11 litros
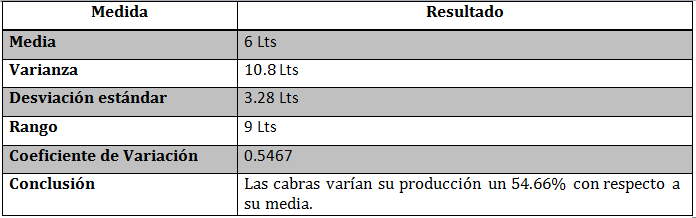
Conclusiones Generales:
El coeficiente de variación para este caso fue de 0.5466. Este dato le puede ser de utilidad al productor al saber en qué cantidad cambia su producción por animal con respecto a su promedio general. Ya que fueron pocos animales la variación fue mayor, debido a que mientras mayor número de unidades experimentales menor será la variación.
Con todos estos puntos claros, es posible pasar a la parte de la elaboración de un modelo de predicciones.
En nuestra vida cotidiana estamos habituados a hacer predicciones. Con nuestra experiencia somos capaces de inferir qué puede ocurrir algo cuando se dan unas determinadas condicionantes. En algunos casos, esta predicción puede ser muy relevante, pues nos ayuda a tomar una decisión
Para hacer estas predicciones se utiliza un modelo de regresión que no es más que un proceso estadístico que se utiliza para estimar variables utilizando un número de variables predictoras para estimar la respuesta o predicción.
Variables predictoras o variables independientes:
Son controladas por el investigador y representan el efecto que se desea estudiar.
Variables dependientes:
También denominada variable respuesta es una variable aleatoria con respuesta probabilística, se le puede asociar un comportamiento probabilístico.En otras palabras las variables x son variables que controla el investigador para poder originar una respuesta que sería la variable y.
Ejemplo:

En el ejemplo anterior la variable x es el tratamiento o el alimento y la variable respuesta es el aumento de peso de los animales.
Correlación:
Es la medida del grado de dependencia de dos o más variables.
La relación entre 2 variables cuantitativas se llama correlación simple.
La relación entre una variable dependiente en función a varias independientes se llama correlación múltiple.
En producción animal se utilizan 2 tipos de correlaciones:
Correlación de Pearson:
evalúa la relación lineal entre dos variables continuas. Una relación es lineal cuando un cambio en una variable se asocia con un cambio proporcional en la otra variable.
Correlación de Spearman:
suele utilizarse para evaluar relaciones en las que intervienen variables ordinales (Bajo, mediano, alto, poco, mucho).
Rangos de correlaciones: 0-0,29 Baja C 0,30-0,69 Media y 0,70-1 Alta.
Valor significativo de R:
Si el P que acompaña al R es menor de 0,05, concluimos que la correlación es significativa y esto indica que es una correlación real y no debida al azar.
El valor de R elevado al cuadrado indica el porcentaje de la variación de una variable debido a la variación de la otra es decir nos da un nivel de confiabilidad.
Correlaciones negativas:
SI la correlación es negativa si la variable x sube la y baja
Correlaciones positivas:
Si una variable sube la otra sube.
Ejemplo del uso de la correlación donde Y es el peso al destete de un rebaño de ovejas.
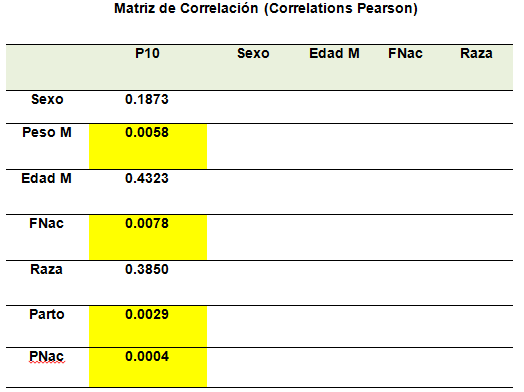
De la matriz anterior, se aprecia que con el peso al destete, sólo se asocian significativamente: el peso de la madre, la fecha de nacimiento, peso al nacer de la cría y el tipo de parto. Asimismo, se aprecia que entre las variables independientes no existen predictores que posean alta correlación (colinealidad) lo cual los hace buenos predictores del peso al destete.
¿Pero qué pasa cuando las variables X o Y son cualitativas?
Ya que la regresión estima el nivel de los cambio de las variables para hacer sus predicciones en caso de ser cualitativas esto se torna más complicados ya que estas no poseen un valor numérico, para este problema se creó un modelo de regresión adaptable a esta situación llamado regresión logística.
El modelo de regresión logística se utiliza cuando la variable respuesta es binaria (solo adopta dos valores posibles)
La característica que se quiere explicar a una cualidad que puede únicamente tomar dos modalidades (modelos binomiales).
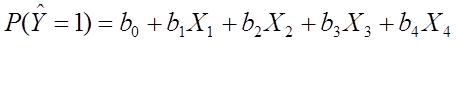
Donde en su ecuación se ve claramente una variable Y (Respuesta) y las variables X (Predictoras) con sus constantes, para entender mejor su uso se hará un ejemplo.
Obtener un índice de selección con base al peso al destete de un rebaño de ovejas donde se prediga que animales llegaran al peso al destete y cuáles no.
Obtener un índice de selección para el peso al destete en función del sexo, peso de la madre, peso de la cría, fecha de nacimiento, raza y tipo de parto.
En función de lo anterior, se procedió a correr una regresión logística para el peso al destete previamente convertido en variable binaria (0;1) en función del peso de la madre, peso al nacer de la cría, fecha de nacimiento y tipo de parto.
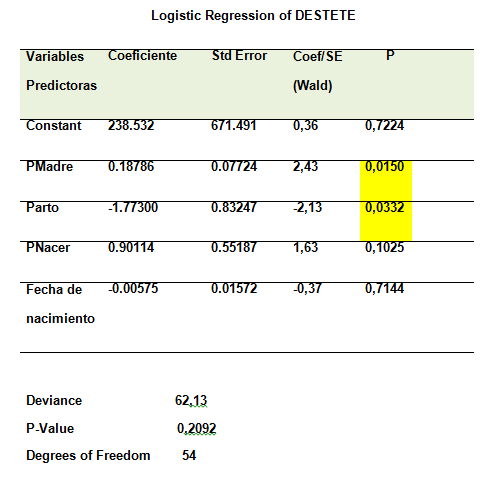
Luego el índice de selección obtenido es:
Dest = 238,532 +0,18786 pmadre - 1,773 parto + 0,90114 pnac – 0,00575 fnac
En el resultado anterior, puede apreciarse que los predictores significativos son peso de la madre y el tipo de parto (ver resaltado)
Este índice se consiguió con los resultados de la regresión logística por destete y usando como base la fórmula de regresión múltiple:
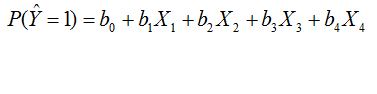
Una vez obtenido el modelo, se debe realizar una prueba de validación del mismo que tiene tres pasos:
Paso1:
Establecer el Sistema Hipotético:
Ho: El modelo es de buen ajuste a los datos.
H1: El modelo es de mal ajuste a los datos.
Este sistema hipotético se prueba con el estadístico de Desviación (que sigue una distribución Chi-Cuadrado). En el presente caso, el estadístico de Desviación está acompañado por un valor P que es mayor de 0,05,
(P-Value= 0,2092) con lo cual la Desviación no es significativa, se procede a no rechazar H_o y, en consecuencia, el modelo es de buen ajuste a los datos.
Paso 2:
Verificar la significación de cada variable predictora, a través del estadístico Wald, con ello se identifica cuales variables contribuyen significativamente al modelo. En el presente caso, los Wald que son significativos son los asociados a las variables predictoras que tengan un valor P<0,05. Así pues, podemos llegar a la conclusión de que las variables que contribuyen significativamente al modelo son: el peso de la madre y tipo de parto. Las variables peso al nacimiento y fecha de nacimiento deben permanecer en el modelo porque aun siendo no significativas contribuyen al buen ajuste del modelo.
Paso 3:
Prueba del poder de predicción del modelo: consiste en tomar al azar una tétrada de valores, esto es, el peso de la madre, tipo de parto, peso al nacer y fecha de nacimiento. Por ejemplo:
Dest = 238,532 +0,18786 pmadre - 1,773 parto + 0,90114 pnac – 0,00575 fnac
Al sustituir los valores de: peso de la madre= 33, tipo de parto= 1, peso al nacer = 3,6 y fecha de nacimiento de 31/10/16, el software procesa la información obteniéndose un valor de Destete=1 (que indica que el animal va a tener un peso al destete igual o superior al promedio del rebaño considerado.
Asimismo, si tenemos un peso de madre igual a 48, tipo de parto igual a 2, un peso al nacer igual a de 2,7 cuya fecha al nacer fue de 31/10/16 el software procesa mediante su algoritmo interno dado por la ecuación obtenida y conduce a un valor de destete igual a cero. El valor del destete en este caso igual a cero, indica que el animal no alcanzará el peso de destete deseado y por tanto no debe continuar en el rebaño debe ser eliminado, porque compromete económicamente el proceso productivo, caso contrario creará perdidas que pueden ser evitadas.
Referencias
[1] Sierra Porta D. (2009) NOTAS DE ESTADÍSTICA Y PROBABILIDAD.
[2] Castejon O. DISEÑO EXPERIMENTAL CON STATISTIX.
[3}
[4}
[5}
[6}
[7}
[8}
[9}
Hola @williamsq te invito a leer el siguiente artículo https://steemit.com/stem-espanol/@carloserp-2000/directrices-sobre-normas-de-derechos-de-autor-en-steemstem-stem-espanol
Gracias por compartir el articulo, eso me ayudara significativamente en próximas publicaciones.
muy interesante, tratare de aplicar algunos de estos conceptos a mi finca!
Aplicando correctamente los conceptos los resultados serán satisfactorios. Te invito a que lo hagas.
¡Felicitaciones tu publicación ha sido seleccionada para recibir el Upvote y Resteem del Proyecto de Curación @Codebyte!
Si deseas apoyarnos y saber mas sobre este proyecto puedes seguirlo y estar atento a sus publicaciones. Ingresando aquí podrás ver el reporte en donde tu publicación ha sido destacada.