ÓPTICA GEOMÉTRICA: Espejos y lentes.
Rayo luminoso: es la línea imaginaria por donde se propaga la luz basandose en el principio de propagación de la luz en línea recta.
Principio de Huygens.
Principio que debe su nombre a Christian Huygens celebre físico y matemático que en 1678 propuso que la luz era un fenómeno ondulatorio, basándose en el concepto de frente de onda.
Este principio nos dice que todo punto de un frente de onda inicial se puede ver como una fuente de ondas esféricas secundarias que se propagan en todas las direcciones con la misma frecuencia, longitud de onda y velocidad que el frente de onda inicial, haciendo uso de esto podemos predecir la posición futura del frente de onda inicial siendo la envolvente de todas las ondas secundarias.
Principio de Fermat.
Principio extremal enunciado por el matemático francés Pierre de Fermat en 1662, establece que la trayectoria que recorre la luz de un punto a otro es tal que el tiempo requerido es mínimo, enunciado de esta forma es útil para muchos casos sin embargo es necesario hacer notar que en algunos casos la luz sigue un camino óptico máximo por lo tanto el principio de Fermat se reformuló como sigue: el trayecto que sigue la luz para propagarse de un punto a otro es tal que el tiempo es estacionario respecto a posibles variaciones de la trayectoria.

Fenómenos de reflexión y refracción.
Las leyes que gobiernan estos fenómenos pueden ser deducidas haciendo uso del principio de Fermat o del principio de Huygens, a continuación procederemos a ello haciendo uso del principio de Fermat.
Reflexion.

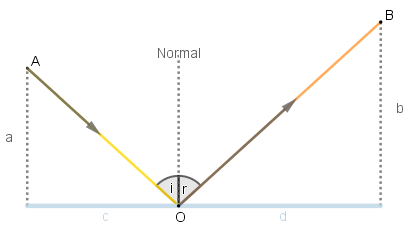
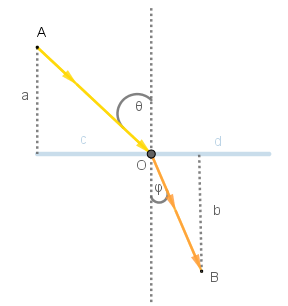
Un rayo incidente que parte de A choca con la superficie reflectante en O, se refleja y sigue una trayectoria hasta B, "O" puede encontrarse en cualquier punto de la recta horizontal, siendo i y r los ángulos de incidencia y reflexión respectivamente.
Definiendo:
Sustituyendo lo anterior en la ecuación para el tiempo obtenemos:
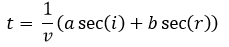
Si movemos ligeramente el punto O los ángulos presentarán una variación di y dr. La variación dt del tiempo vendrá dada por:
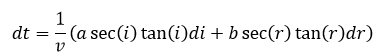
Como los diferenciales de los ángulos no son independientes entre sí de la figura se deduce que:
Derivando ambos miembros:
Combinando lo anterior con la condición del tiempo mínimo obtenemos:
Refraccion.
Entonces procediendo como en el caso anterior:
Si movemos ligeramente el punto O los ángulos presentarán una variación dθ y dφ. La variación dt del tiempo vendrá dada por:
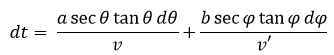
Si el tiempo es mínimo dt = 0 entonces:
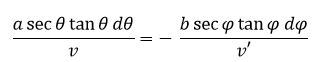
Al ser c + d constante tenemos:
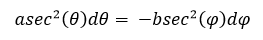
Dividiendo (1) entre (2) obtenemos:

Construcción de imágenes en espejos. (Objeto no puntual)
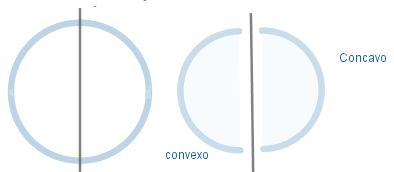
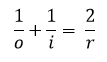
- Centro de curvatura: es el centro de la esfera teórica a la cual pertenece nuestra superficie.
- Radio de curvatura: es el radio de dicha esfera.
- Eje principal: es la recta que une el centro de curvatura con el centro de nuestro espejo.
- Foco: es el punto sobre el eje donde convergen todos los rayos que inciden paralelos al eje.
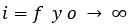
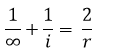
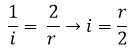
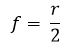
Lo que nos dice que, en los espejos esféricos el foco esta ubicado a una distancia de la mitad del radio de curvatura, lo que es igual al punto medio entre el vértice del espejo y el centro de curvatura.
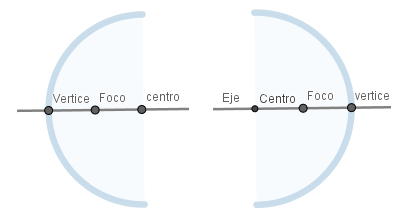
En la imagen de arriba podemos ver la ubicación de los elementos del espejo para los dos casos, en el espejo cóncavo el radio de curvatura es menor que cero r < 0 y en los convexos tenemos r > 0
Propiedad de reversibilidad:
- Un rayo que incide paralelo al eje pasa por el foco y viceversa.
- Un rayo que pase por el centro de curvatura se regresa por el mismo camino pero en sentido inverso debido a que la incidencia es perpendicular.
Ejemplos espejos cóncavos:
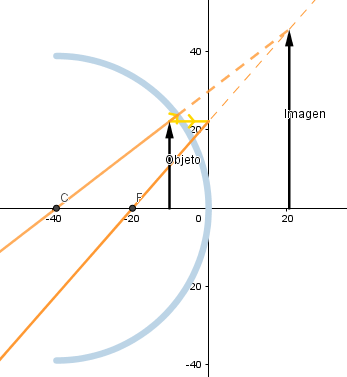
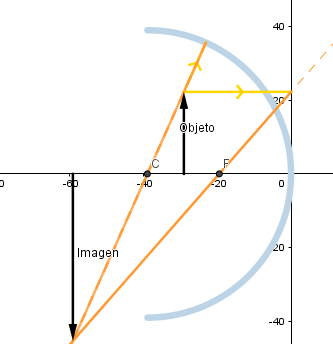
Objeto situado delante del foco.
Como podemos ver si el objeto se encuentra situado a una distancia menor que la distancia focal la imagen que se forma es virtual, debido a que es generada por la prolongación de los rayos reflejados además de esto su tamaño será mayor que el del objeto.
Objeto situado en el foco.
Cómo podemos observar los rayos son paralelos entre sí y por ende nunca convergen por lo cual no se forma imagen.
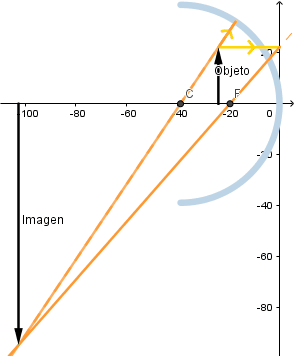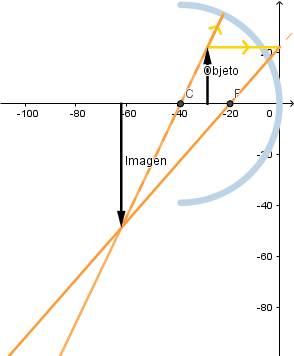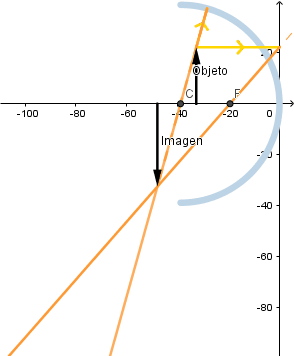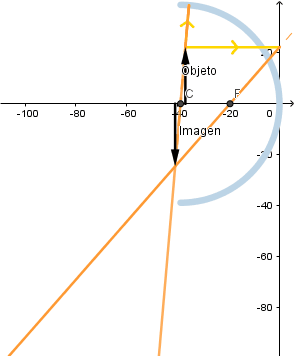
Objeto situado entre el foco y el centro de curvatura.
Como se ve la imagen que se forma es real, de mayor tamaño que el objeto e invertida, es decir la imagen se verá al revés.
Al estar el objeto entre el centro de curvatura y el foco e irse acercando el objeto al centro de curva la imagen va disminuyendo su tamaño.
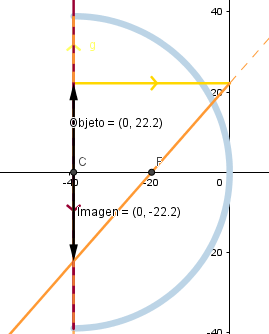
Objeto en el centro de curvatura.
La imagen formada es real, de igual tamaño que el objeto pero invertida.
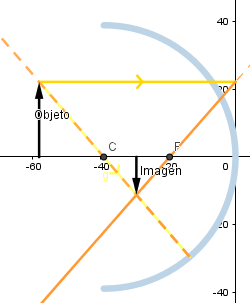
Objeto más allá del centro de curvatura.
Se observa que la imagen formada es invertida, de menor tamaño que el objeto y real.
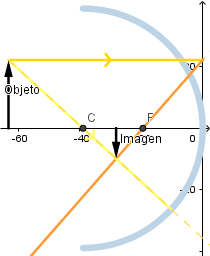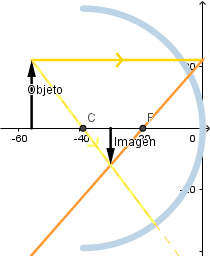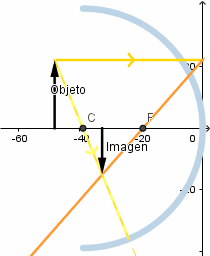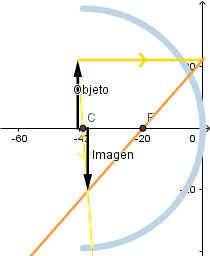
Mientras mas alejado este el objeto del vertice del espejo el tamaño de la imagen es menor.
Ejemplo espejo convexo.
Como se puede ver en los espejos convexos sin importar la ubicación del objeto la imagen siempre sera de menor tamaño que el objeto y virtual ya que al estar el centro de curvatura y el foco "detrás" del espejo la imagen es formada por las prolongaciones de los rayos y no puede ser recogida en una pantalla, ejemplos cotidianos de espejos convexos son los usados en los retrovisores de los automóviles.
La imagen en espejos planos es virtual, derecha y de igual tamaño que el objeto. Cuando los rayos de luz chocan contra el espejo se reflejan y divergen como si procedieran de un punto P' situado detrás del plano del espejo, cuando estos rayos entran en el ojo no pueden distinguirse de los rayos que procedieran de una fuente luminosa situada en P' sin que hubiese espejo.

Construcción de imágenes en lentes.
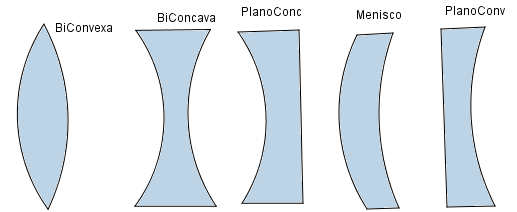
En óptica una lente es un dispositivo capaz de desviar los rayos de luz, es decir, de causar una refracción y tenemos dos tipos de ellas:
- Lentes convergentes: estas son más gruesas en el centro y estrechas en sus bordes, se les denomina así porque todos los rayos que inciden paralelos al eje convergen en el foco, las lentes convergentes son lentes convexas o combinaciones de estas.
- Lentes divergentes: contrario a las convergentes son más gruesas en los bordes y presentan estrechez en el centro, se denominan así porque dispersan o hacen diverger todo rayo que incida en ella paralelo al eje y son las prolongaciones de estos los que convergen en el foco, estás lentes son cóncavas
La construcción de las imágenes en las lentes se puede realizar siguiendo las siguientes propiedades; en las lentes convergentes todo rayo que incide en la lente paralelo al eje se refracta pasando por el foco imagen (F'), todo rayo que pase por el foco objeto (F) emerge paralelo al eje y todo rayo que incida pasando por el centro óptico (centro geométrico de la lente) emerge sin desviarse, en las lentes divergentes estás reglas cambian un poco, todo rayo que incida en la lente paralelo al eje es la prolongación del rayo que emerge la que paso por el foco objeto y de igual forma todo rayo que incida pasando por el centro óptico emerge sin desviarse.
Ejemplos lente biconvexa.
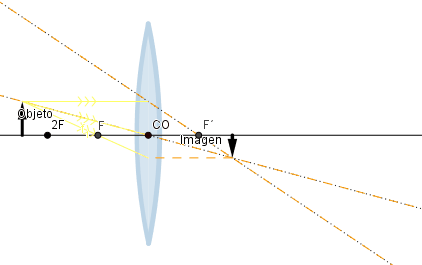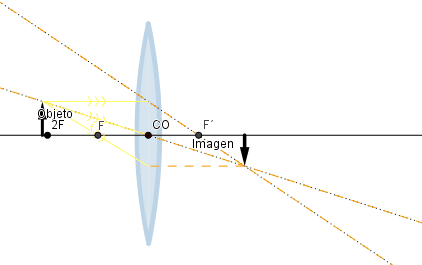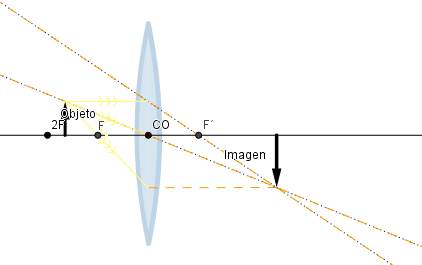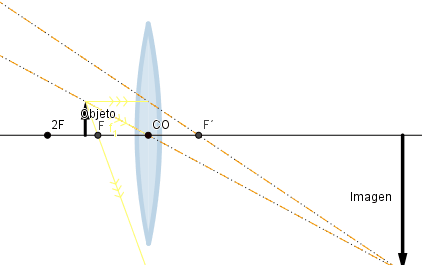
Objeto situado más allá de la distancia focal.
Como se puede observar a medida que el objeto se acerca al foco el tamaño de la imagen aumenta pero sigue siendo inferior a la del objeto, esto cambia cuando el objeto se encuentra a una distancia mayor que la distancia focal pero menor a dos veces la distancia focal en ese intervalo el tamaño de la imagen es mayor que la del objeto pero sigue manteniendo su naturaleza real e invertida.
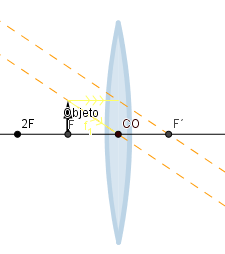
Objeto situado en el foco.
En este caso no se forma imagen los rayos nunca convergen en un punto.
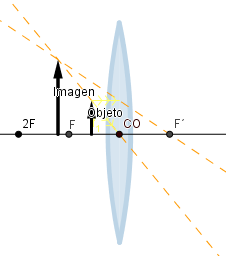
Objeto situado a una distancia menor que la distancia focal.
Como podemos ver aquí la naturaleza de la imagen cambia, se vuelve virtual y ya no está invertida además que su tamaño es mayor que la del objeto.
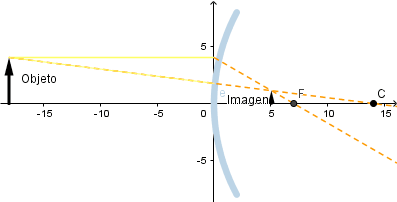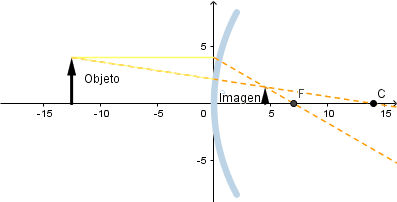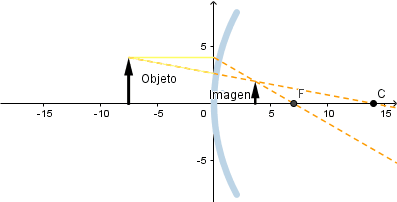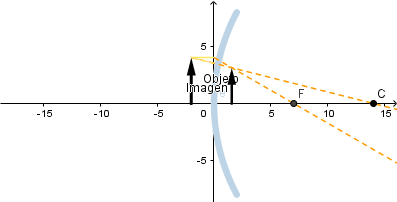
Ejemplo lente bicóncava.
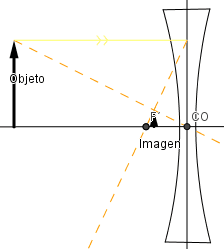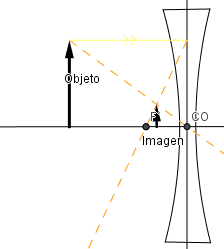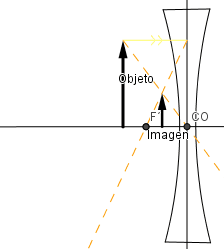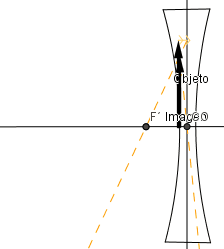
Conclusiones generales:
- El ángulo de reflexión es igual al ángulo de incidencia.
- Todo rayo qué incida paralelo al eje se refleja pasando por el foco y viceversa.
- La luz siempre recorre un camino óptico extremo (máximo o mínimo)
- Los espejos cóncavos son convergentes y los convexos divergentes.
- En los espejos convexos la imagen siempre es virtual, derecha y de menor tamaño que el objeto.
- Las lentes bicóncavas son divergentes y las biconvexas convergentes.
- En la lente bicóncava la imagen siempre es virtual, derecha y menor tamaño que el objeto.

Espero hayan disfrutado de este fascinante tema, si así fue estén atentos a mi próxima publicación ;).
Material consultado:
Resnick, Halliday, Krane, (1992). Física Vol. 2. 4ta edición compañía Editorial Continental México.
Rodríguez, I., Lacasta, A., (1997). Apuntes de fisica I de topografía. Escuela Politécnica de Barcelona. https://ocw.upc.edu/sites/all/modules/ocw/estadistiques/download.php?file=27102/2009/1/53095/40788-3277.pdf
Font, J. (2003). Óptica geométrica. Universidad Politécnica de Cataluña. http://aransa.upc.es/ffettsi/Apuntes/Optica.pdf
(2016). Imagen de un objeto puntual: refracción en una superficie esférica. http://materias.df.uba.ar/f2byga2016c2/files/2012/07/RESUMEN_Deducci%C3%B3n-de-las-leyes-de-reflexi%C3%B3n-y-refracci%C3%B3n.pdf
Óptica geométrica. I.E.S Silverio Lanza departamento de física y química. http://www.educa.madrid.org/web/ies.silveriolanza.getafe/Ens/DptoFisicaQuimica/Bachillerato/Optica11May09.pdf
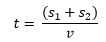
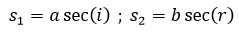
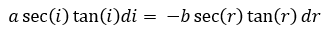
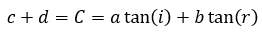
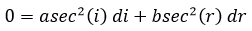
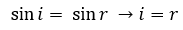
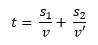
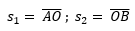
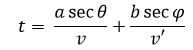
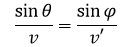
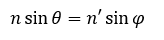

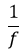
A ver... la verdad, el tema me gusta lo justito... pero...
viendo el trabajo de maquetación que te has pasado, creando además los gráficos, bien se merece un upvote y el reconocimiento expreso.
Suerte y éxito!!!
Te he mencionado en mi Reto curación: Posts Votados y sugeridos 29/Mayo.
Excelente trabajo @luiscd8a. Impecable tu explicación. Esas imágenes hablan por si sola. Un gran aporte el trabajo que realizaste.
Muchas gracias profesor @lorenzor, estoy aprendiendo de los mejores ;)
Excelente post muy didactico y facil , felicidades me gusto mucho los gifs
Muchas gracias, la idea de las imágenes y GIF's es esa, que se pueda comprender todo de manera más sencilla.
Congratulations @luiscd8a!
Your post was mentioned in the Steemit Hit Parade for newcomers in the following category:
I also upvoted your post to increase its reward
If you like my work to promote newcomers and give them more visibility on Steemit, feel free to vote for my witness! You can do it here or use SteemConnect
Me hiciste recordad mis clases recibidas en bachillerato. Luego de eso no tuve mucho contacto con esta parte de la física ya que en el programa de la carrera de Ingeniería lo removieron.
Mucho después mi hija se graduó de optometrista y tuve acercamiento a esta parte de la física.
Siempre me llamó la atención por ejemplo, el fenómeno y explicación de como se forman las imágenes reflejadas.
Tiene mucha explicación técnica tu publicación que me agrada. Las imágenes y la animación son espectaculares. Saludos.
Felicitaciones por ese trabajo tan bien presentado.
Es un area sumamente interesante y con grandes aplicaciones, tuve la oportunidad de estudiarla un poco el semestre pasado y las prácticas de laboratorio fueron lo mejor!!
Gracias por tan agradable comentario @profeyer
Éste tema es muy complejo y llamativo, solo por el título... Además de que lo reflejas bien detallado en tus imágenes. Increíble, saludos. Tienes mi upvote, sigue así!
Es un tema por demás interesante además de que se nos presenta a diario. Gracias por tu apoyo @ggeraldooso
Definitivamente esto si es contenido de calidad.
Muchas gracias!!!
Hi @luiscd8a!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Excelente!!! Muchas gracias.
muy bueno este articulo... excelente!
Muchas gracias por pasar a leerlo.
Me parece genial el uso de las herramientas tecnológicas para presentar el tema de geometría óptica que impacta por el movimiento de tus imágenes, te felicito.
Hay que hacer uso de los recursos que tenemos para explicar de la mejor forma posible! Saludos @azulear gracias por tu comentario.