Ondas mecánicas: ondas sonoras y efecto Doppler.
En mi publicación anterior sobre ondas mecánicas nos enfocamos en las ondas transversales y a partir de ellas deducimos la función de onda, dijimos que también la onda podía ser longitudinal sin embargo dejamos de lado este tipo de onda, hoy nos enfocaremos en ella y veremos la gran importancia que tiene en nuestro día a día.
Recordemos que una onda mecánica del tipo longitudinal es aquella en la cual las partículas del medio por el cual se propaga la onda se mueven en el mismo sentido de propagación que esta, un ejemplo clásico de esto es el caso que tengamos un tubo lleno de un fluido; supongamos que es un gas, en el extremo izquierdo del fluido tendremos un pistón el cual moveremos con un movimiento armónico simple su movimiento ocasionará que las partículas que conforman el gas se muevan de igual forma en movimiento armónico simple.

(Todas las imágenes y GIF's fueron hechos por mi usando el software matemático GeoGebra Classic 5.)
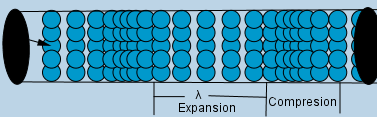
Lo anteriormente dicho se puede ver ejemplificado en el GIF, el pistón simulado por la flecha empuja al gas conformado por sus partículas, vemos como la onda se propaga hacía la derecha y las partículas se mueven hacía delante y hacía atrás en la misma dirección de propagación siendo una onda longitudinal, algo muy interesante que podemos observar es que hay zonas donde las partículas se agrupan y zonas más despejadas esto representa zonas de mayor y menor presión respectivamente.
El pistón al empujar el gas lo comprime disminuyendo su volumen y haciéndo que la presión aumente al devolver el pistón a su posición original el volumen aumenta y la presión disminuye, estos cambio de presión se van propagando a lo largo de todo el fluido. Si realizamos una comparación con la onda senoidal que ya conocemos los puntos de máxima presión y mínima presión son los puntos de cero desplazamiento.
(Todas las imágenes y GIF's fueron hechos por mi usando el software matemático GeoGebra Classic 5.)
La onda longitudinal aquí creada se rige por la función de onda 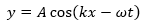 que antes estudiamos, sin embargo al observar los cambios de presión resulta conveniente expresar su comportamiento en estos términos.
que antes estudiamos, sin embargo al observar los cambios de presión resulta conveniente expresar su comportamiento en estos términos.
Consideremos un tren continuo de compresiones y rarefacciones viajando en el tubo lleno de gas su ecuación de onda es:
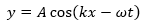
Debido a que consideramos las fluctuaciones de presión 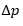 = y ; definimos la cantidad conocida como módulo volumétrico:
= y ; definimos la cantidad conocida como módulo volumétrico:
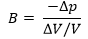
Al despejar tenemos que:
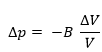
Si consideramos una capa de fluido a la presión inicial esta tiene un espesor 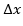 un área A y su volumen es
un área A y su volumen es 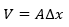 . Cuando la presión cambie su volumen será
. Cuando la presión cambie su volumen será 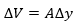 (compresión).
(compresión).
Si 
Al sustituir y realizar las operaciones correspondientes tenemos:
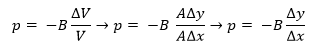
En el límite diferencial:
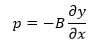

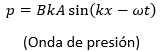
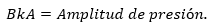
La velocidad viene dada por 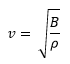 al despejar B y sustituir en lo anterior podemos reescribir la ecuación de la siguiente forma:
al despejar B y sustituir en lo anterior podemos reescribir la ecuación de la siguiente forma:
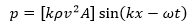
ONDA DE PRESIÓN.

Sonido: ondas sonoras.
Las ondas sonoras son las causantes del efecto que conocemos como sonido, estas son ondas mecánicas longitudinales y se propagan desde la fuente en todas las direcciones; al propagarse van creando variaciones en la presión en el ambiente por arriba y por debajo de la presión atmosférica con la misma frecuencia del movimiento qua las partículas perturbadas en el aire, nuestro oído funciona detectando estás variaciones de presión, la onda al entrar en el oído crea estás fluctuaciones y hace vibrar nuestro tímpano lo que se traduce en sonido.
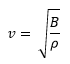
Sabiendo estos valores podemos calcular la velocidad del sonido por ejemplo en el aire:
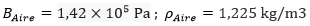
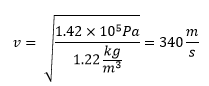
Y para el agua tenemos:
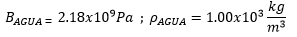
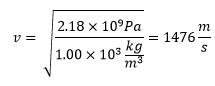

Efecto Doppler.
Fuente en reposo y receptor en reposo:
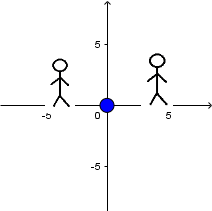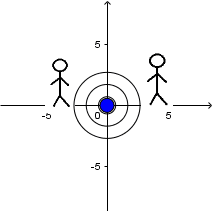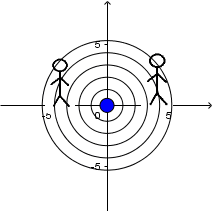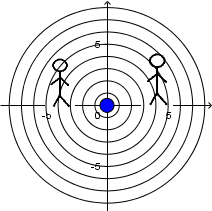
(Todas las imágenes y GIF's fueron hechos por mi usando el software matemático GeoGebra Classic 5.)
Fuente en reposo y el receptor en movimiento:
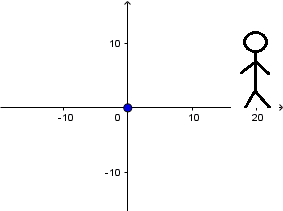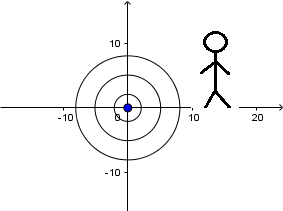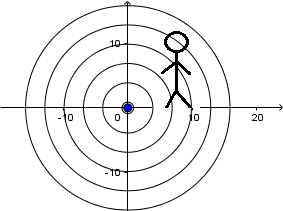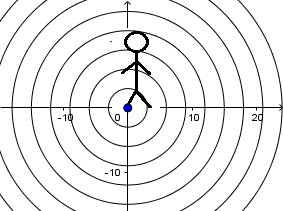
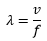 siendo v la velocidad de propagación de la onda en el medio, al estar el receptor en movimiento estas ondas llegan a el con una velocidad relativa
siendo v la velocidad de propagación de la onda en el medio, al estar el receptor en movimiento estas ondas llegan a el con una velocidad relativa 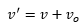 siendo
siendo 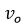 la velocidad del observador, así que la frecuencia
la velocidad del observador, así que la frecuencia
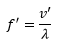
Que resulta en:
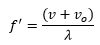
Al sustituir el valor de lambda obtenemos:
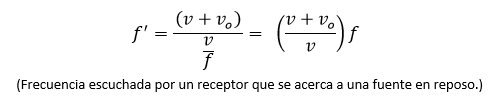
Fuente en movimiento y receptor en movimiento:
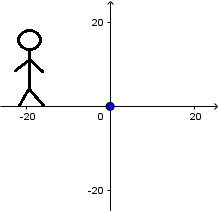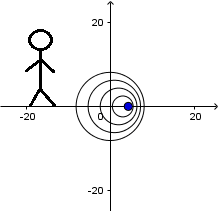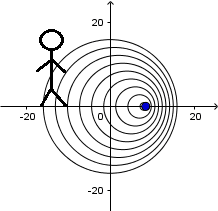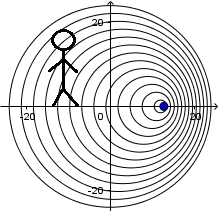
Delante de la fuente la longitud de onda es:
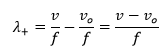
Y detrás de la fuente:
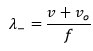
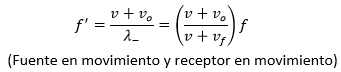
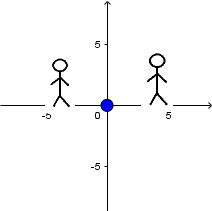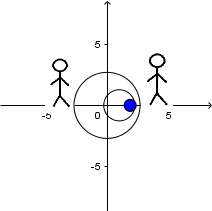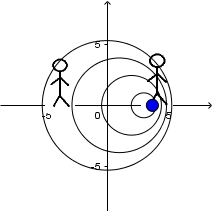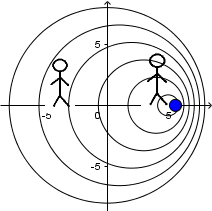
Fuente en movimiento con velocidad menor a la del sonido y receptor en reposo:
Procediendo para el observador situado detrás de la fuente:
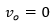 debido a que el observador está en reposo obteniendo:
debido a que el observador está en reposo obteniendo: 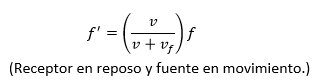
Procediendo para el observador situado delante de la fuente:
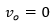 . La diferencia es que ahora en el dedominador tendremos
. La diferencia es que ahora en el dedominador tendremos 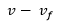 debido a que las ondas se emiten moviéndose en la dirección negativa del receptor a la fuente. Obtenemos:
debido a que las ondas se emiten moviéndose en la dirección negativa del receptor a la fuente. Obtenemos:
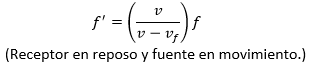
Fuente en movimiento a una velocidad sónica y receptor en reposo:
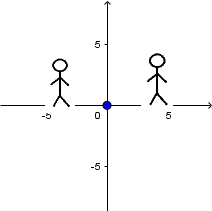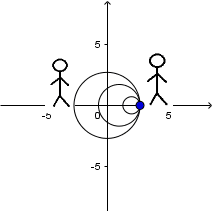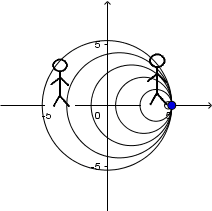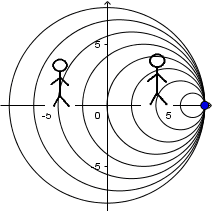
Fuente en movimiento con una velocidad supersónica y receptor en reposo:
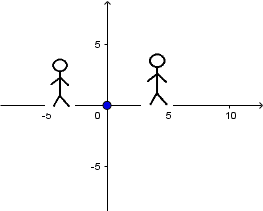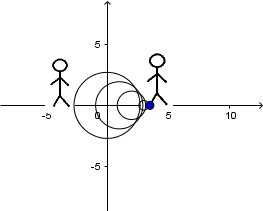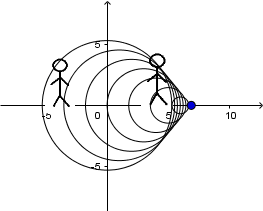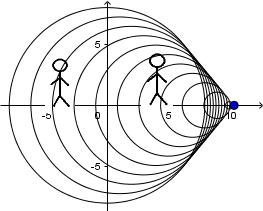
Conclusiones generales:
Las partículas en las ondas longitudinales se mueven en el mismo sentido de propagación de la onda.
Las ondas sonoras son ondas longitudinales y de presión.
Las ondas sonoras se propagan en todas las direcciones por lo cual se pueden ver como frentes de ondas esféricos.
La frecuencia de una onda sonora se traduce en el tono del sonido que escuchamos.
Una frecuencia alta es un sonido agudo y una frecuencia baja un sonido grave.
Para que se produzca el efecto Doppler debe existir movimiento relativo entre la fuente y el receptor.
Un receptor que se acerca a la fuente escucha una frecuencia mayor a la emitida originalmente por la fuente.
Un receptor que se aleja de la fuente escucha una frecuencia más baja a la emitida originalmente por la fuente.
Si la fuente se acerca al receptor este escuchará una frecuencia más alta y si se aleja una más baja.
El cono de Mach se produce a velocidades supersónicas.

Espero hayan disfrutado de este tema y del interesante efecto Doppler, si desean leer más artículos sobre ciencia los invito a visitar la etiqueta #stem-espanol
(Todas las imágenes y GIF's fueron hechos por mi usando el software matemático GeoGebra Classic 5.)
Material consultado:
Resnick, Halliday y Krane (1993), Física. 3ra edición Compañía Editorial Continental México Volumen 1.
Young, H. D, & Freedman, R. A. FISICA UNIVERSITARIA, volume 1. Pearson Educación de México, S.A. de C.V., 2009.
Tippens, P. E. FISICA - CONCEPTOS Y APLICACIONES. McGrawHill/Interamericana Editores, S.A. DE C.V., 7ma edition, 2001.
Hola @luiscad8a. Me surgió una curiosidad: ¿Podrías decirme qué relación tiene este efecto Doppler con el llamado "Boom sónico"?
Buen post!
Guardan mucha relación @eniolw el boom sónico se produce cuando la fuente viaja a velocidades supersónicas en el último GIF puedes ver este caso, las ondas que se van formando detrás de la fuente interfieren constructivamente entre sí con lo cual generan una onda de amplitud muy grande llamada onda de choque cuando esto sucede se escucha este "estampido sónico", la onda de choque se produce por el movimiento de la fuente como tal.
En la ecuación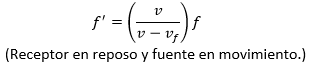 te podrás dar cuenta que, cuando la velocidad de la fuente es igual a la del sonido se produce una singularidad ya que el denominador sería cero y en el momento que la velocidad de la fuente supera a la del sonido tendríamos una frecuencia negativa lo cual no tiene sentido físico, cuando estás singularidades ocurren se produce este fenómeno.
te podrás dar cuenta que, cuando la velocidad de la fuente es igual a la del sonido se produce una singularidad ya que el denominador sería cero y en el momento que la velocidad de la fuente supera a la del sonido tendríamos una frecuencia negativa lo cual no tiene sentido físico, cuando estás singularidades ocurren se produce este fenómeno.
Espero haber respondido tu inquietud, tenía pensado explicar esto en otra publicación jajaja. Saludos.
Excelente men tienes que enseñarme como usar el software GeoGebra jejeje
Gracias @gerardoalfred, he estado pensando publicar unos pequeños tutoriales sin embargo no soy experto, los GIF's los logro después de una jornada de ensayo y error.
Que gratificante leer post de calidad, Es la Onda¡¡(expresión que usamos en México para decir fantástico¡)
Muchas gracias por tu comentario @viper160891 ha sido la onda! ;)
Hi @luiscd8a!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Excelente aporte para entender mejor las ondas, me gustaria contactar contigo para que desarrollemos el diseño de un micro reactor nuclear, usando ideas modernas, creo que tendras mucho interes desarrollando ese tema. mi tlf +58 -4141256633.