(Todas las imágenes han sido hechas por mi usando el software matemático GeoGebra Classic 5.)
Saludos estimados lectores en especial a los que me leen de la comunidad de
#STEM-espanol, luego de estar algunas semanas alejado debido a problemas con mi PC y la conexión a Internet estoy de vuelta con esta nueva publicación; donde profundizaremos un poco más en las superficies minimales y los recorridos mínimos en busca de ampliar mi post
anterior, el cual recomiendo dar un vistazo antes de continuar con esta lectura, en esta oportunidad comprobaremos una vez más como la naturaleza siempre intenta minimizar los costos de energía buscando los caminos más eficientes.
Anteriormente vimos como las fuerzas de cohesión de los líquidos actúan haciendo que las moléculas se atraigan unas con otras ocasionando que las situadas en la superficie del líquido reciban una fuerza neta hacia al fondo de este, produciendo la
tensión superficial. Además en busca de reducir su energía al mínimo los líquidos tienden a mostrar un área superficial mínima; esto pudimos comprobarlo con unos simples experimentos sumergiendo en una disolución jabonosa una estructura y viendo que la película de jabón formada entre sus límites era
una superficie minimal.
Antes de adentrarnos más en este tema definamos un par de conceptos...
- Recorrido mínimo:
es el problema donde se busca conseguir un camino entre dos vértices de tal modo que la suma de las longitudes de los aristas que lo constituyen es mínima.
- Punto de Fermat:
es un punto donde la distancia total desde él a los vértices de un triángulo es mínima, este problema fue planteado por Pierre de Fermat a Evangelista Torricelli el cual lo resolvió y solución fue publicada por su pupilo en 1659.
Entonces si queremos saber cual es el recorrido mínimo para los vértices de un triángulo solo basta conseguir su punto de Fermat, veamos como podemos hacerlo.
Se tiene un triángulo equilátero:
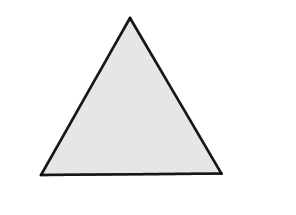
Para determinar la ubicación de su punto de Fermat empezaremos construyendo triángulos en cada uno de sus lados:
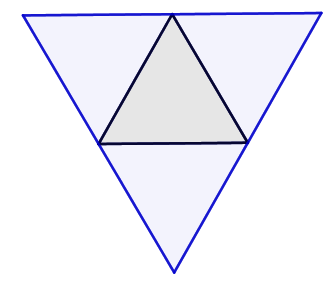
Luego, desde cada nuevo vértice de cada triángulo se traza una recta hasta el vértice opuesto del triángulo inicial:
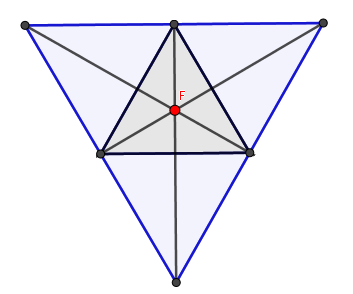
El punto donde estas rectas convergen es el
punto de Fermat,
una vez ubicado el punto, el recorrido mínimo que conecta los vértices del triángulo inicial no es más que el trazado por las aristas que unen sus vértices con el punto de Fermat:
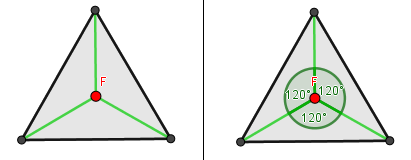
Entre todos los caminos posibles el que hace que el recorrido entre los vértices del triángulo sea mínimo es el anterior encontrado el cual pasa por el punto de Fermat, podemos ver además que el ángulo formado entre cada segmento es de 120°.
Determinar el punto de Fermat no se limita a un triángulo equilátero, podemos encontrar el respectivo punto de Fermat utilizando este método para cualquier triángulo en el cual ninguno de sus ángulo internos supere los 120°.
Ejemplo:
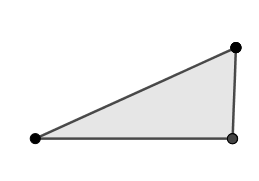
De la misma forma que antes construimos triángulos a cada lado del triángulo inicial:
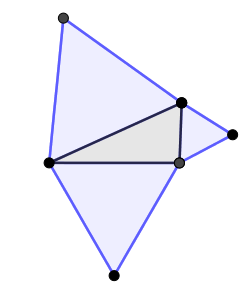
Luego de esto trazamos una recta desde cada nuevo vértice de los triángulos creados a el vértice opuesto del triángulo inicial:
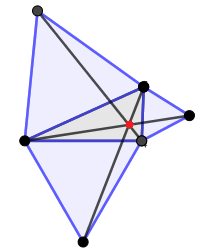
Y hemos localizado nuevamente el punto de Fermat y el recorrido mínimo para este triángulo:
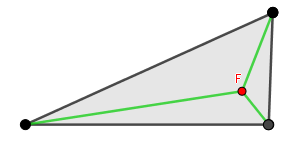
Este método puede ser ampliado para otras figuras que no sean un triángulo, por ejemplo un cuadrado:
En este caso lo primero que debemos hacer es ubicar el centro del cuadrado:
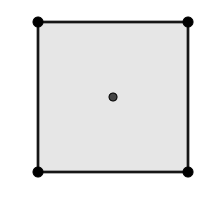
Para encontrar el recorrido mínimo que une los vértices, procedemos a crear un triángulo en el interior uniendo dos vértices con el centro del cuadrado:
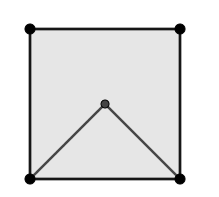
Hecho esto simplemente encontramos el punto de Fermat para este triángulo como lo hemos hecho anteriormente:
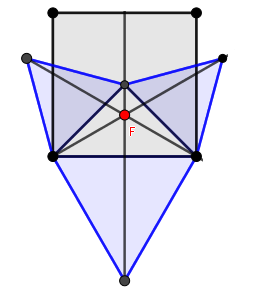
Ubicado el punto de Fermat podemos trazar el recorrido mínimo para la mitad del cuadrado y por simetría este es el mismo para la otra mitad, por lo tanto obtenemos:
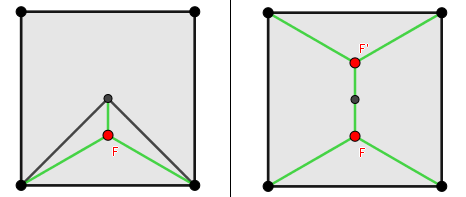
Recorrido mínimo para un cuadrado.
La idea del recorrido mínimo se suele extrapolar al problema en el cual se requiere construir una red de carreteras que conecte a ciudades no alineadas entre si, el camino encontrado seria el mas optimo pues significaría una disminución del material a utilizar, ademas se puede plantear el problema en que se necesite construir un hospital que de cobertura a tres ciudades, el lugar mas optimo donde construirlo seria ubicado en el punto de Fermat, esto obviando el número de habitantes en cada ciudad. También podríamos imaginar el caso en que sea necesite realizar un tendido eléctrico, de fibra óptica o casos afín.
Comprobación experimental.
Lo anterior puede ser comprobado experimentalmente de forma sencilla haciendo uso de la tensión superficial, para esto necesitaremos:
- Recipiente con agua jabonosa.
- Dos láminas transparentes.
- Ramplugs.
Luego de tener los materias necesarios simplemente pegamos perpendicularmente los ramplugs a una de las láminas formando un triángulo equilátero, luego pegamos sobre ellos la otra lámina.
Realizada la estructura procedemos a introducirla dentro del recipiente con agua de jabón de forma que quede totalmente sumergida, al sacarla se habrán creado películas de jabón entre los ramplugs:
(Todas las fotos han sido realizadas por mi con mi teléfono celular Siragon SP-5050.)
Como podemos ver el camino trazado por las películas de jabón es exactamente el mismo que encontramos anteriormente y efectivamente existe un ángulo de 120° entre cada película.
Lo anterior no es casualidad, pues la formación de las películas de jabón así como las burbujas de jabón y la manera en que se distribuyen se rigen por las leyes de Plateau, en lo anterior podemos comprobar la primera de estas leyes la cual está enunciada de la siguiente forma:
"Tres superficies de jabón se intersecan a lo largo de una línea. El ángulo formado por los planos tangenciales a dos superficies que se intersecan, en cualquier punto a lo largo de la línea de intersección de las tres superficies, es de 120 grados".
Recorrido mínimo para un cuadrado:
Podemos comprobar el recorrido mínimo para este caso de la misma forma que antes, solo que ahora construiremos la forma de un cuadrado entre las láminas plásticas:
Se puede ver como las películas de jabón construyen el mismo camino que anteriormente encontramos para el cuadrado, si procedemos a medir los ángulos entre películas podemos ver que son de 120°.
Recorrido mínimo para un hexágono.
Se observa que no se crean conexiones de tres películas entre sí como en los demás casos, la razón de esto es que los ángulos internos del hexágono ya son de 120° y el recorrido mínimo para sus vértices es simplemente el mostrado. En casos particulares las películas pueden formar otro "recorrido mínimo" pero estos representan una longitud mayor hasta de 4% que la anterior mostrada.
Figura creada al expandir una burbuja dentro del hexágono.
Superficies mínimas.
Las superficies minimales son aquellas que tienen una curvatura media nula, su nacimiento se remonta a Lagrange el cual se preguntó cuál sería la superficie
de menor área extendida, en busca de una respuesta obtuvo como solución el plano, años después en 1776 Meusnier demostró que el helicoide y la catenoide son superficies minimales. Durante 1830-1865 se realizaron amplios avances en esta área y actualmente se conocen una amplia variedad de superficies mínimas.
Podemos aprovechar el comportamiento de los líquidos para formar superficies mínimas sumergiendo estructuras dentro de la disolución de jabón, al retirarla las películas de jabón forman una superficie mínima entre los límites de la estructura, la formación de esta superficie de igual forma se rige por las Leyes de Plateau.
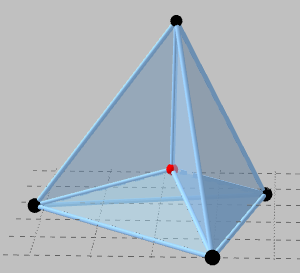
Superficie mínima para un tetraedro.
Si observamos con cuidado podemos ver en la figura anterior 4 segmentos que parten desde los vértices del tetraedro y convergen en un punto, estos segmentos son las aristas y el punto donde convergen es el baricentro, este es el equivalente al punto de Fermat en 3D.
Debido a que creo que en la foto no se puede apreciar la genialidad de la superficie me dispuse a crear esta animación 3D para ustedes:
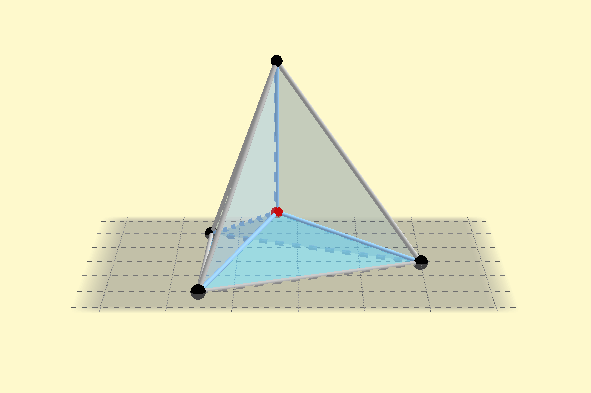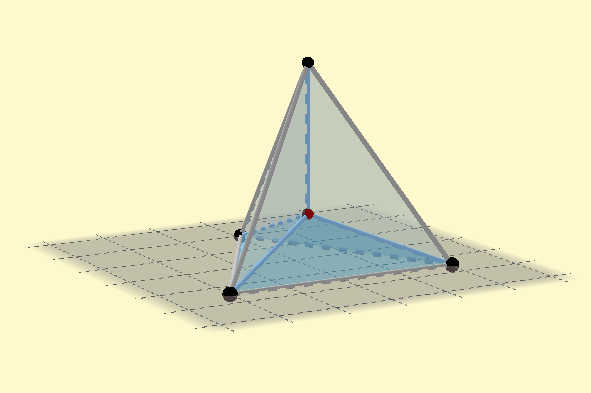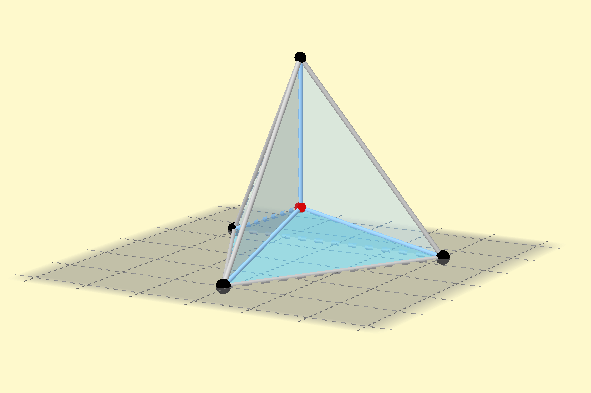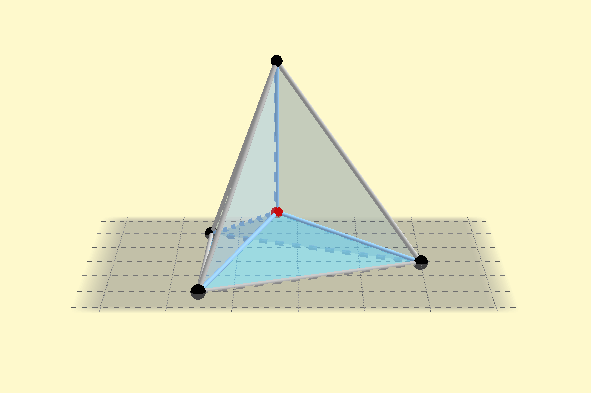(Animación 3D hecha por mi con el software matemático GeoGebra Classic 5.)
Parte inferior de la superficie:
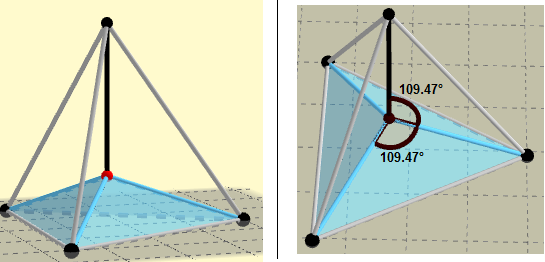
Podemos ver en la parte inferior tres láminas de jabón divididas por tres aristas que convergen en el baricentro, el ángulo entre las aristas coincide con la segunda Ley de Plateau quedando así comprobada, la cual se enuncia de la siguiente forma:
"Cuatro de las líneas, todas formadas por la intersección de tres superficies, se intersecan en un punto y el ángulo formado por cada par de ellas es de 109.47°".
Parte superior de la superficie:
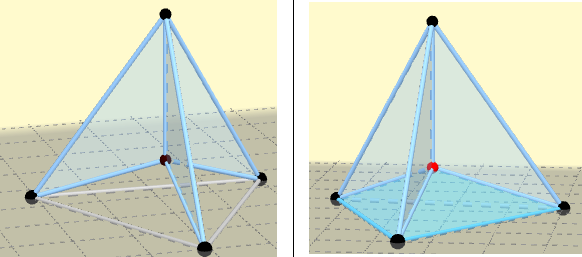
La parte superior está formada de igual forma por tres láminas de jabón, estas apoyadas sobres las aristas inferiores y divididas por la arista que parte del vértice superior a la base y que converge igualmente en el baricentro. La superficie total está formada entonces por seis películas de jabón divididas por cuatro aristas.
Otras superficies mínimas.
Superficie mínima entre dos aros concéntricos: catenoide.
Superficie mínima para un cubo.
Las superficies mínimas siguen siendo estudiadas por la ingeniería molecular y la ciencia de materiales en busca de su implementacion, ademas de estar involucradas en complejas teorías como la de agujeros negros y ser usadas por parte de diseñadores y arquitectos.
Conclusiones generales:
- El punto de Fermat es un punto ubicado donde la distancia total desde los vértices de un triángulo a él es mínima.
- El baricentro es la representación en 3D del punto de Fermat.
- El ángulo entre dos películas de jabón es de 120° (Primera Ley de Plateau).
- El ángulo entre las aristas de una superficie de jabón es de 109.47°(Segunda Ley de Plateau).
- El orden y la forma que adoptan las burbujas, superficies y laminas de jabón se rigen por las Leyes de Plateau.
Material consultado:
- T. Soldovieri, (2017), Introducción a la mecánica clásica, Venezuela, 1era edición.
- Bragado, Juan. Películas de jabón y superficies mínimas. http://www.juanbragado.es/ficheros/Mis%20trabajos%20para%20la%20web/Superficies%20m%C3%ADnimas.pdf
- Punto de Fermat.
- Superficie minimal.
(Todas las imágenes han sido hechas por mi usando el software matemático GeoGebra Classic 5. Todas las fotos han sido tomadas por mi con mi teléfono celular Siragon SP-5050).
Espero hayan disfrutado de este interesante tema, si así fue pueden dejarme su comentario.
Si deseas leer contenido sobre ciencia te invito a visitar la etiqueta #STEM-espanol y si estas interesado en publicar contenido de Física, te invito cordialmente a unirte al sub-grupo #fisica del chat de stem-espanol en discord.
Créditos @djredimi2
Congratulations @luiscd8a! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
As a follower of @followforupvotes this post has been randomly selected and upvoted! Enjoy your upvote and have a great day!
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Oh, muy bien post, @LuisCD8a. Es llamativo como compruebas experimentalmente la teoría. La imagen GIF también es llamativa y hace más didáctico el contenido. Por cierto, no le coloques puntos a los títulos y subtítulos (norma en español). Saludos!
Congratulations @luiscd8a! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Congratulations @luiscd8a! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Hola @luiscd8a, no conocía esta temática, me llama la atención el detalle y la especificidad con la que presentas el contenido, precisamente apto para el autoaprendizaje de la comunidad científica que hace vida en Steemit!! Te felicito!! Saludos cordiales!!
Congratulations @luiscd8a! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPCongratulations @luiscd8a! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Congratulations @luiscd8a! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard: