PROCESO DE PRECIPITACION MULTIFASE: MODELOS FENOMENOLOGICOS, SIMULACION MONTE CARLO Y COMPARACION EXPERIMENTAL MEDIANTE MEDIDAS DE PODER TERMOELECTRICO EN ALEACIONES Fe-C
Estimados Amigos de Steemit:
Acá les presento un trabajo que realicé en conjunto con colegas de la Universidad de Oriente y que considero un tema de interés en el área de la física del estado Sólido y de Ciencia de los Materiales.
En este trabajo se simula mediante el método Monte Carlo la cinética de transformación de una solución sólida homogénea, sobresaturada después de tratamiento térmico, con la formación de fases metaestables y estable, usando una versión macroscópica del modelo de Binder donde no se consideran los intercambios atómicos que implican el crecimiento y decrecimiento de clusters sino que se toman en cuenta los cambios en estos como entes macroscópicos o clusters en las diferentes fases consideradas.

Se comparan los resultados de la simulación con medidas experimentales de poder termoeléctrico en sistema Fe-C y también con otros métodos para resolver analítica y fenomenológicamente el proceso de formación de fases en soluciones sólidas antes mencionadas

Muchas teorías han intentado de explicar formalmente los cambios de fase que ocurren en un material tanto desde el punto de vista microscópico como macroscópico.
Teoría microscópica:
la teoría estadística de Binder et al (1) basada en el modelo de clustering, que explica la formación de fases mediante los mecanismos de coagulación y evaporación en clusters por saltos de los átomos en la solución sólida y que es la más compleja en este aspecto.
Teorías macroscópicas:
Cahn (2) Chávez (3) y Luiggi (4) propusieron aproximaciones clásicas al estudio de las variaciones de la energía libre de Gibbs asociadas a los cambios de fase como una alternativa válida para caracterizar la dinámica del sistema que también conduce a la resolución de sistemas de ecuaciones diferenciales de gran complejidad.
Modelo de Precipitación Multifase:
Luiggi et al. (5) presentaron una versión simplificada de la teoría microscópica de clustering, basada en los principios básicos de la teoría de nucleación y crecimiento, reduciendo el problema de tener resolver tantas ecuaciones como átomos difunden en la búsqueda del equilibrio a tener que dar sólo tantas ecuaciones como fases coexistan en el proceso.
Modelos empíricos-fenomenológicos:
los criterios son característicos de los modelos y no de la cinética, ya que cada uno de ellos reporta resultados muy disímiles, por lo que se puede evaluar el rango de validez de cada modelo en mediante los datos isotérmicos obtenidos por propiedades sensibles a los cambios estructurales tales como la resistividad eléctrica y el poder termoeléctrico en aleaciones.
En este trabajo se simula el proceso de precipitación multifase de una aleación supersaturada mediante método Monte Carlo acoplando la teoría de Binder (1) con la aproximación dada por Luiggi en el modelo cinético multifase (5) y para ello se han escogido operadores de ocupación equivalentes a las diferentes fases que intervengan en el proceso y la dinámica se realiza mediante tantas “caminatas aleatorias” como fases se consideren usando un modelo semejante al de Ising del magnetismo pero donde los operadores de ocupación en lugar de representar spines hacia arriba o hacia abajo, representan la fase (homogénea, metaestable o estable) del sitio de la red. Esto hace el modelo muy poderoso ya que permite obtener resultados numéricos válidos sin el problema de resolver sistemas de ecuaciones extremadamente complejos y permite considerar tantas fases metaestables como se quiera con solo considerar otros operadores de ocupación.
Se comparan los resultados de la simulación con datos experimentales de poder termoeléctrico en las aleaciones Fe-C mediante cálculos de la fracción total precipitada que han sido obtenidos de la literatura y realizados por el Grupo de Física de Metales del Departamento de Física de la Universidad de Oriente en el 2008, respectivamente.
De la ecuación maestra que describe los procesos de intercambio atómico (ec. 1) se puede derivar la ecuación maestra que describe la evolución temporal de los clusters patrones, que resulta para l>1:
donde se ha denotado la probabilidad de que los clusters con l y l’ sufran coalescencia por unidad de tiempo por y la reacción inversa (de ruptura) por .
Para l=1, se obtiene una ecuación similar, sólo que los términos contenidos en las sumatorias sobre l’ que van hasta l-1 se omiten.
El significado físico de cada término se da a continuación:
I) El primer término toma en cuenta la ganancia de clusters debido a todas las reacciones de ruptura l+l’→(l,l’).
II) El segundo término describe la perdida de clusters l debido a todas las reacciones de ruptura l→(l-l’,l’). El factor ½ toma en cuenta los pares de (l’,l-l’) en la suma.
III) El tercer término describe la ganancia de clusters l debido a todas las reacciones de coalescencia (l’,l-l’). Una ecuación de balance ha sido usada para relacionar la razón de este proceso con su inverso.
IV) El último término describe la perdida de clusters l debido a todas las reacciones de coalescencia (l,l’) →l+l’.
Modelos empíricos- Fenomenologicos
La literatura reporta varios modelos empírico-fenomenológicos que relacionan la evolución temporal de la fracción transformada en una aleación sólida después de un proceso térmico. Estos modelos son representados por la siguiente ecuación:
donde k=k0exp(-Q/Rt) cumple la ley de Arhenius y k0 es un valor constante, Q es la energía de activación, t es el tiempo de envejecimiento, R es la constante de los gases, T es la temperatura absoluta de envejecimiento y p es el exponente de afectación. En la tabla I se resumen algunos de los modelos de reacción más conocidos. Si p=0, se obtiene la ecuación Jonhson- Mehl- Avrami (JMA), si p=1, la ec. (2 ) representa la ecuación de Austin-Rickett (AR). El exponente del tiempo n frecuentemente se asocia con el proceso de crecimiento, el cual ha sido usado por algunos investigadores para establecer un vínculo entre ese exponente y la forma y/o talla de los precipitados.
MODELO CINÉTICO DE PRECIPITACIÓN MULTIFASE
Luiggi (5) plantea obtener la evolución de la fracción trasformada en la solución sólida Fe-C, de la siguiente manera: Considera una solución sólida la cual, en su proceso de transformación, exhibe una fase metaestable caracterizada por su fracción transformada, designada Z, y una fase estable caracterizada por su fracción transformada U. La fracción total transformada es Y=U+Z=1-y, donde y es la fracción total no precipitada
Para el tiempo de envejecimiento t a temperatura T, la fracción precipitada se calcula usando la siguiente relación
Poder termoeléctrico
Un gradiente de temperatura en una muestra puede estar acompañado por un campo eléctrico directamente opuesto a dicho gradiente, lo que es conocido como efecto Seebeck. La razón entre el campo electrostático y el gradiente de temperatura se denomina Poder Termoeléctrico (PTE).La ecuación de Mott relaciona el PTE difusional con la resistividad eléctrica ρ y su derivada respecto a la energía evaluada en el nivel de energía de Fermi
SIMULACIÓN MONTE CARLO DE LA TRANSFORMACIÓN MULTIFASE:
Hay N*N clusters, siendo N la dimensión de la matriz que representa al material sometido a proceso térmico. Inicialmente la muestra es homogénea y por lo tanto cada cluster también lo está. En este modelo se asigna a cada cluster un operador de ocupación μi =0 y por lo que toda la matriz está totalmente llena de ceros. Se comienza la simulación y en cada interacción (que representa la evolución temporal del sistema) se escoge aleatoriamente un cluster que cambia (o no) de fase.
Al comenzar el proceso térmico, el i-eximo cluster escogido al azar se encuentra en fase homogénea Y, lo que se representa como un sitio de la matriz ocupado por μi =0 y de acuerdo al esquema tiene dos probabilidades: transformarse con probabilidad P1 en un cluster en fase meta estable Z, lo que se representa por μi =-1 o transformarse en un cluster en fase estable U, lo que se representa como μi =1(con probabilidad P2). En las subsiguientes iteraciones el cluster escogido estocasticamente puede estar en cualquiera de las fases, en el caso de estar en fase homogénea se procede como se describió anteriormente, en caso de escogerse un cluster en fase metaestable Z (μi=-1), este tendrá la probabilidad de transformarse en un cluster de fase homogénea Y (μi=0) (con probabilidad P3) o transformarse en un cluster de fase estable U (μi=1) (con probabilidad P4). En el caso de escogerse un cluster en fase estable U (μi=1), este no sufrirá transformación y se procede a la siguiente interacción.
Resultados y Discusión
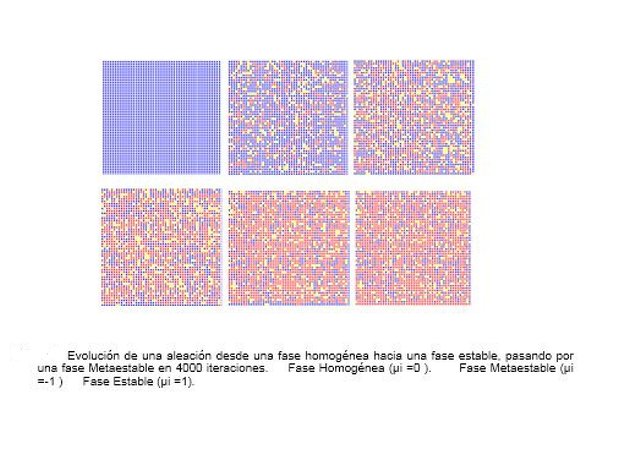
En este parágrafo se muestran los resultados de la simulación Monte Carlo del proceso de precipitación multifase en aleaciones, para ello se elaboró un programa en Fortran 77 en el cual se codificó el proceso descrito en el capítulo anterior. Se uso la subrutina RAND de Numerical Recipes (33) para generar números aleatorios tanto en la escogencia del cluster que sufre la transformación como en los sorteos esquematizados en la figura 5. El programa para visualización de la evolución de matriz se realizó en Fortran 99 que imprime un cuadro rojo cuando el cluster está en fase homogénea (μi =0), un cuadro amarillo cuando esté en fase metaestable (μi =-1) y un cuadro azul cuando esté en fase estable (μi =1).
Referencias:
1- Binder K; Stauffer D. Z. (1976).Physik B, 24, 207.
2- Cahn J. W.(1961). Acta Met. 9,795
3- Chàvez E. Trabajo de Ascenso para Titular. LUZ. 2010
4- Luiggi N.;Chávez E. (1987) Phys. Rev. B, 36, 9528.
5- Luiggi N.; Betancourt A.,(1994), Metall Trans. B, 25, 917.
Excelente trabajo @emily61, aquí se destaca la originalidad e importancia de la investigación científica que combina la simulación y la experimentación. El estudio del coeficiente Seebek para determinar la potencia termoeléctrica de los materiales es, en estos momentos, muy importante en el desarrollo de la ciencia de los materiales.
Gracias amigo @iamphysical por el apoyo. Me alegra mucho que te haya gustado.
Sufriendo con los apagones y las caidas de internet.
Me párese interesante este post @emily61. Saludos.
Gracias. Que bien que también te guste la física. Saludos
Sneaky Ninja Attack! You have just been defended with a 2.39% upvote!
I was summoned by emily61. I have done their bidding and now I will vanish…
woosh
P.S. If you or anyone you know has been a victim of @grumpycat please know that he has been harming people throughout Sōsharumedia (ソーシャルメディア). Stealing the service that I (and other bots) have provided them and hiding behind a facade of stopping bid bot abuse which he clearly has no interest in.
Sneaky Ninja is a very responsible bot, working directly with steemcleaners, actively pursuing spam and abuse on our platform. If you would like to see what steps Sneaky Ninja has taken to fight bid bot abuse see this post and this post. Also know that I am working daily on other solutions.
If you would like to know my personal take on bid bot abuse and why I do not agree with the 3.5 day rule, see this post
Grumpycat is a villain that must be stopped to protect our freedoms here on steemit!
There is a resistance that has formed to counter his tyranny.
If you would like to take an active role in stopping this menace and helping other victims like yourself...

Learn More Here
I have also summoned my love, Kusari to offer some limited help to victims like you.
See Here
Muy buen trabajo mi muy hermosa colega @emily61. Buen aporte al conocimiento científico. Saludos.
Que bueno que esta plataforma brinda una oportunidad para que mostrar que hacemos. Saludos