COMPRENDIENDO EL MECANISMO DE UN TERREMOTO DESDE LA ÓPTICA DE LA TEORÍA DEL REBOTE ELÁSTICO Y DE MODELOS EMPÍRICOS QUE RELACIONAN LA MAGNITUD DE MOMENTO “Mw” CON PARÁMETROS CARACTERÍSTICOS DEL PLANO DE FALLA
Saludos a todos los usuarios de STEEMIT y muy especialmente a mis compañeros de #stem-espanol. Escribir sobre tópicos relacionados con la ingeniería sismoresistente es algo que me apasiona, porque es un excelente camino para seguir aprendiendo y mejorando en esta hermosa rama de especialización de la ingeniería civil. En una publicación anterior (ref. 07), realicé un contraste sobre las diversas formas de medir el tamaño de un sismo, y abordé las ideas generales de cómo estos se originan. En esta oportunidad, realizaremos un breve repaso por estos temas, para luego adentrarnos de lleno, en la estimación de los parámetros geométricos que constituyen un plano de falla a partir del conocimiento de la magnitud de momento “Mw”. Con la intención de hacer didáctico el proceso de disertación de las ideas, he desarrollado varios esquemas conceptuales que permiten una visión global de las temáticas tratadas. Los esquemas conceptuales son de mi autoría, señalando en la fuente las herramientas computacionales que contribuyeron a su elaboración. Con mucho cariño, para todos ustedes, disfruten de los contenidos que a continuación se exponen:
INTRODUCCIÓN
La sismología como ciencia que se encarga del estudio de los terremotos, nos regala un amplio campo de aprendizaje sobre estos fenómenos que forman parte de la dinámica de nuestro planeta. En esta oportunidad, profundizaremos en los mecanismos que originan los terremotos de foco superficial, dedicando especial atención a las fallas transcurrentes, un tipo de falla que caracteriza la interacción entre la placa Suramericana y la placa del Caribe, y por ende los mecanismos de fallas de Boconó, San Sebastián y el Pilar, responsables de los principales terremotos que han azotado a Venezuela, avanzando de este modo en el conocimiento de la sismicidad del país.
Imagen N°01: ideas generales a estudiar
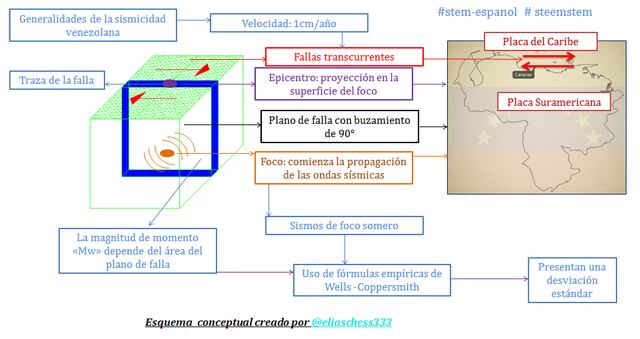
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint, Paint y AutoCAD 2007. La imagen del mapa de Venezuela es de dominio público y la misma puede visualizada en el siguiente link: https://pixabay.com/es/contorno-mapa-venezuela-geograf%C3%ADa-322489/
Teniendo claras la nociones generales que caracterizan la sismicidad venezolana, ahondaremos en los parámetros de los que depende el momento sísmico “Mo”, cuyo conocimiento es importante para el cálculo de la magnitud de momento “Mw”, un dato clave para la estimación empírica de los parámetros geométricos del plano de falla (longitud, profundidad) a través del uso de las relaciones de Wells y Coppersmith; hecho que constituye el objetivo de este artículo; consistente en adquirir la habilidad de que con el conocimiento de “Mw”, demos un paso adelante en la determinación de la geometría del plano de falla involucrado; y así ampliar nuestra visión, hacia este tipo de fenómenos, como lo son los terremotos.
DELIMITACIÓN DE LA TEMÁTICA A ESTUDIAR
De acuerdo a lo que se aprecia en las imágenes N°01 y N°02, estaremos delimitando las aplicaciones de este trabajo a los sismos cuyo mecanismo de origen se adaptan a la teoría del rebote elástico propuesta por Reid en el año 1910, por lo que estaremos tratando sismos de foco superficial, tomando como referencia el sismo de Caracas con una profundidad “h= 14 km” y el sismo de Cariaco con una profundidad “h= 9.4 km” (ver referencias N°05 y N°06). Si hacemos un viaje a la profundidad de la tierra (ver imagen N°02), nos daremos cuenta, que estos sismos de foco superficial, están ocurriendo en la parte superior de la litosfera, aproximadamente en los primeros 15 km a 20km de su espesor; lo cual corresponde a una parte de la litosfera constituida por rocas de gran dureza, capaces de tener un comportamiento elástico ante la aplicación de importantes esfuerzos, inducidos por el movimiento relativo entre bloques tectónicos, centrándose este estudio en las fallas de naturaleza transcurrente, que se dan cuando un bloque tectónico se desplaza lateralmente con respecto al otro.
Imagen N°02: una visión didáctica de la teoría del rebote elástico
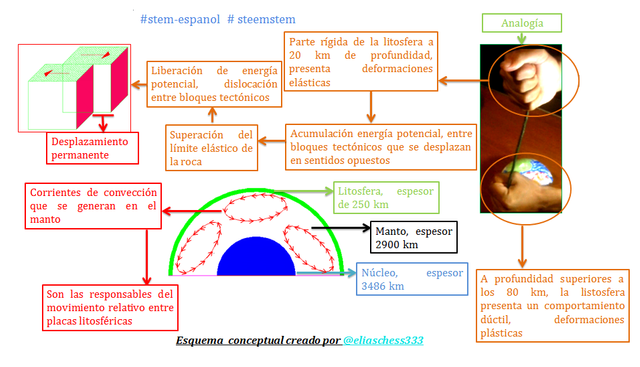
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint, Paint y AutoCAD 2007. La imagen utilizada para la analogía fue capturada con mi dispositivo Tablet VIT-T4000.
Este desplazamiento obedece al hecho de que las rocas de la parte profunda de la litosfera presentan un comportamiento dúctil ante las corrientes de convección que se dan en el manto; dicho desplazamiento induce una deformación elástica en la parte rígida de la misma; lo cual extrapolado al caso de una falla transcurrente (ver imagen N°01), es una deformación que se presenta entre los bloques tectónicos que rodean el plano de falla y se da en sentidos opuestos; lo que se traduce en acumulaciones significativas de energía potencial de deformación.
Una gran acumulación de energía potencial de deformación, sugiere una superación del límite de elasticidad de la roca “μ”, lo que redunda en que se produce una falla frágil en la misma, liberando toda la energía potencial acumulada, disipándose un 90% en calor y el otro 10% en forma de ondas sísmicas, que en la superficie son percibidas como terremotos, y que produce desplazamientos permanentes, como se aprecia en el gráfico resaltado por el recuadro de color “rojo” del esquema conceptual de la imagen N°02.
Vale destacar que este es un proceso recurrente, y una vez liberados los esfuerzos, comienza nuevamente el proceso de acumulación de energía potencial. En el caso del sistema de fallas venezolano, descrito en la introducción, la velocidad del movimiento relativo entre bloques tectónico, es de aproximadamente 1cm/año; no por ello, podemos subestimar la ocurrencia de sismos importantes en nuestro país.
Otro aspecto a delimitar en este trabajo, es que de las amplias escalas de magnitud utilizadas para medir el tamaño de un sismo, estaremos utilizando aquella que se denomina Magnitud de Momento “Mw”, la cual más allá de los registros de un sismograma, depende de la configuración geométrica del plano de falla que dio origen al terremoto, por lo que no sufre saturación, es decir, puede detectar sismos de magnitudes superiores a 9. Te invito a que revises la referencia N°07, donde realizo un contraste entre las principales escalas de magnitud que existen y un viaje a la profundidad de la tierra, donde describo su estructura de forma más detallada.
Vale destacar que la escala de Magnitud de Momento “Mw” fue desarrollada por Hanks y Kanamori en el año de 1979, y su cálculo se resume en la aplicación de la siguiente ecuación:
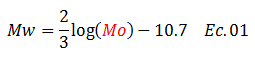
Donde el término “Mo” es conocido como momento sísmico, se sustituye en “dinas.cm”, depende de los parámetros geométricos involucrados en el plano de falla y del límite elástico de la roca “μ”; viene dado por la siguiente ecuación:
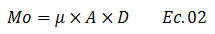
Donde “A” se asocia al área de ruptura, “D” al desplazamiento permanente entre los dos bloques tectónicos (ver imagen N°05) que se produce una vez superado el límite elástico de la roca “μ”, el cual para fines prácticos lo estaremos considerando como:
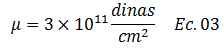
En la referencia N°07, se realiza la deducción de la ecuación N°01. En esta oportunidad profundizaremos en el sustento matemático de la ecuación N°02, y en el uso de fórmulas propuestas por Wells-Coppersmith en el año de 1994, que nos permiten inferir empíricamente aspectos relacionados con las dimensiones del plano de falla, a partir del conocimiento de la magnitud de momento “Mw” del sismo en cuestión.
ABORDAJE MATEMÁTICO DEL CONCEPTO DE MOMENTO SÍSMICO
Basados en el comportamiento elástico en la parte superior de la litosfera, por parte de las rocas que la constituyen, vale la pena introducir el concepto de elasticidad de Young, donde a grandes rasgos se establece la proporcionalidad que existe entre esfuerzos y deformaciones, y que viene dado por la siguiente ecuación:
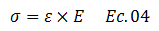
Donde “ε” es la deformación elástica, “E” el módulo de elasticidad del material involucrado, y “σ” el esfuerzo elástico que se está produciendo.
Imagen N°03: ilustración del modelo de doble par de fuerzas
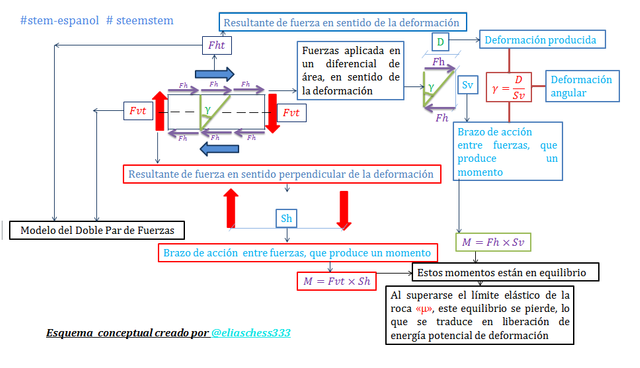
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
Extrapolemos ahora, cada uno de estos términos al problema en estudio, tomando como referencia el esquema conceptual de la imagen N°03, donde:
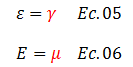
Por lo tanto:
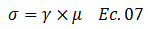
Lo que significa que la deformación angular viene dada por:
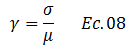
Otra forma interesante de expresar la deformación angular “γ”, es a través del principio del ángulo infinitesimal, que plantea lo siguiente:
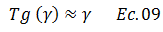
De esta manera:
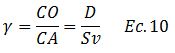
La fuerza neta aplicada a un diferencial de área “Fh” viene dada por:
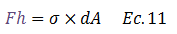
Sustituyendo las ecuaciones N°07 y N°10 en la ecuación N°11 obtenemos:
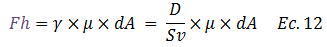
Procedemos a integrar toda el área “A” del plano de ruptura, para obtener la fuerza resultante “Fht”. En este caso el límite superior de integración se representa de modo didáctico por el área de todo el plano de falla. Si deseas profundizar en integrales definidas te invito a la revisión de la referencia N°08, donde el compañero @ydavgonzalez hace una explicación magistral al respecto.
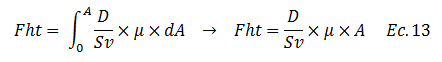
La fuerza resultante en el sentido de la deformación “Fht” se encuentra en equilibrio (ver imagen N°03), siendo la separación “Sv” entre estas fuerzas, el brazo que produce el siguiente momento:
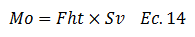
Sustituimos la ecuación N°13 en la N°14 de la forma:
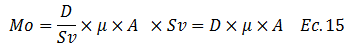
Siendo “Mo” el momento sísmico, base para el cálculo de la magnitud de momento “Mw”, tal como se observa en la ecuación N°01. Vale destacar que las fuerzas resultantes perpendiculares al sentido de la deformación, también producen un momento, en sentido opuesto al anteriormente deducido y del mismo valor; lo que hace que el sistema esté en equilibrio mientras se acumula energía de deformación; la pérdida de este equilibrio, se traduce en liberación de dicha energía causante de los terremotos.
La comprensión de la naturaleza del Momento Sísmico “Mo” es de importancia, dado que nos revela que la magnitud de momento “Mw” está íntimamente vinculada a los parámetros del plano de falla. Esto permitió a Wells y Coppersmith en el año de 1994, desarrollar una serie de relaciones empíricas, donde a partir del conocimiento de la magnitud de momento “Mw”, podemos delimitar geométricamente la zona concerniente al plano de falla, y así tener mayores nociones cuantitativas de la magnitud de un sismo. Por lo que te invito a la lectura del siguiente tópico.
INTRODUCCIÓN A LAS FÓRMULAS DE WELLS-COPPERSMITH
Estas fórmulas que a continuación se presentan, son el resultado de un gran esfuerzo por parte de Wells y Coppersmith, dirigido al estudio de las diversas magnitudes de los sismos ocurridos en el mundo y de las características geométricas de los planos de fallas causantes de los mismos; para así construir una importante data, que con el adecuado tratamiento estadístico y técnicas de regresión, permitieron obtener las relaciones que se ilustran en los esquemas conceptuales de las imágenes N°04 y N°05. Por la naturaleza del origen de estas fórmulas, las mismas están asociadas a una desviación estándar.
Imagen N°04: fórmulas de Wells y Coppersmith para el cálculo de “RLD y SRL”
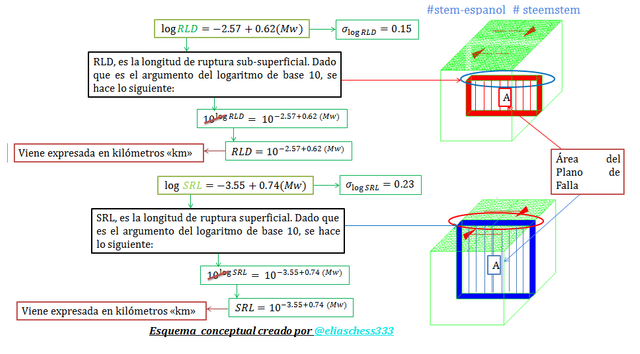
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint, Paint y AutoCAD 2007.
Imagen N°05: fórmulas de Wells y Coppersmith para el cálculo de “RW y D”
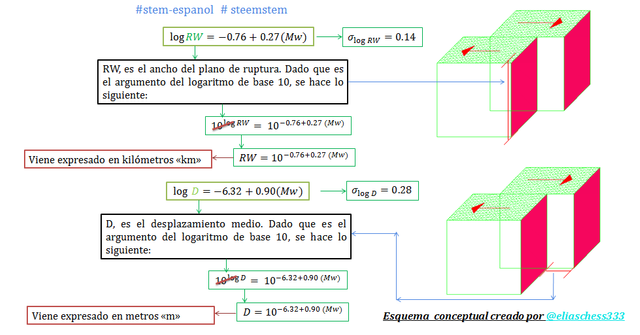
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint, Paint y AutoCAD 2007.
La desviación estándar, permite establecer un rango de posibles resultados, para los parámetros geométricos del plano de falla, sumándose y restándose, como se muestra en las ecuaciones N°16 y N°17, a través del término resaltado en color “naranja”:
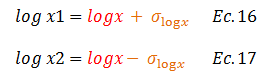
El término resaltado en color “rojo” hace referencia a la constante que resulta de las operaciones algebraicas de las fórmulas expuestas en las imágenes N°04 y N°05. Para obtener el valor de “x1 y x2” las ecuaciones N°16 y N°17, se tratan de la siguiente manera:
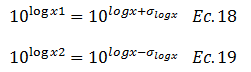
Rescribimos ambas ecuaciones:
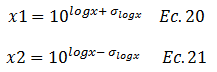
Basados en la siguiente ley de potenciación:
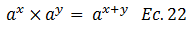
Las ecuaciones N°20 y N°21 se rescriben de la siguiente forma:
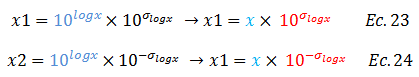
El valor de “x” resaltado en color “azul”, es el que se obtiene directamente de las aplicaciones de las ecuaciones ilustradas en los esquemas conceptuales de las imágenes N°04 y N°05. Dicho resultado debe ser multiplicado por el término resaltado en color “rojo”, para así obtener el rango posible de valores producto de la desviación estándar de cada una de estas fórmulas; de allí a que una forma práctica de presentar estos resultados es la siguiente:
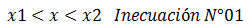
Hasta este momento, hemos desarrollado los planteamientos teóricos que nos llevan a comprender el mecanismo de origen de los terremotos, y a profundizar en las características geométricas de los planos de falla, por lo que te invito a la aplicación de estas ideas expuestas.
APLICACIONES DE INTERÉS TOMANDO COMO REFERENCIA LOS SISMOS DE CARACAS DE 1967 Y CARIACO DE 1997
Caso N°01: sismo de Caracas, año: 1967, sub-evento 2, Mw=6.4, profundidad al foco de 14 km
Este sub-evento, fue el que causó los daños a los centros urbanos de Caracas, donde destaca la zona de Altamira. La traza de la falla no afloró en la superficie, fue un sismo de foco superficial, originado por una falla de tipo transcurrente. Todos estos argumentos, permiten aplicar las relaciones de Wells y Coppersmith (1994).
En este orden de ideas, la longitud de ruptura sub-superficial “RLD” viene dada por:
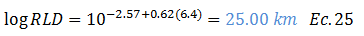
Aplicamos el concepto de desviación estándar:
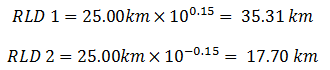
Por lo tanto:
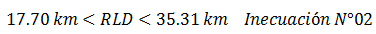
Procedemos a calcular el ancho del plano de ruptura “RW”:
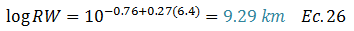
Estimamos el posible rango de valores, haciendo uso de la desviación estándar:

Calculamos ahora el desplazamiento producido, producto de la superación del límite elástico “μ” de la roca:
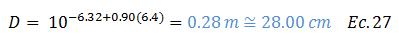
La desviación estándar viene dada por:
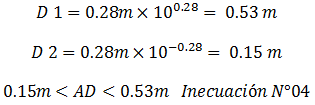
No obstante en la estimación del momento sísmico “Mo” tomaremos como referencia el valor medio resaltado en color “azul” de las ecuaciones N°25,N°26 y N°27. A continuación se presenta de manera didáctica un resumen de los principales resultados obtenidos:
Imagen N°06: resumen de parámetros geométricos del plano de falla, para el caso de estudio N°01
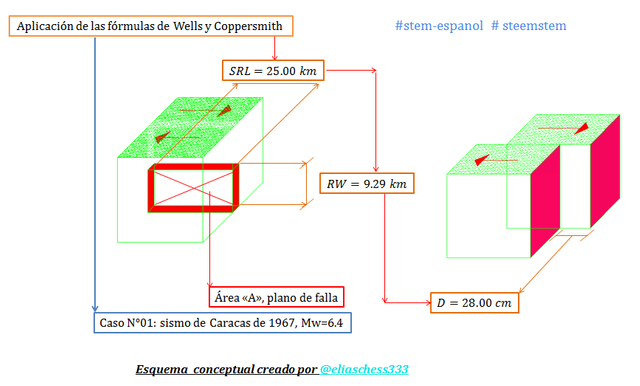
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint, Paint y AutoCAD 2007.
De acuerdo a lo ilustrado en el esquema conceptual de la imagen N°06 el área de ruptura “A” viene dada por:
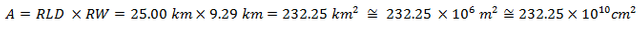
Basados en la ecuación N°02, el momento sísmico “Mo” es:
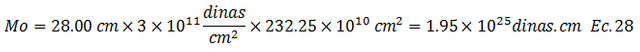
Estimamos la magnitud de momento aproximada “Mw aprox”, aplicando la ecuación N°01, y sustituyendo el momento sísmico “Mo” en unidades de “dinas.cm”, obtenido con los datos del plano de ruptura que arrojan las relaciones de Wells y Cooppersmith:
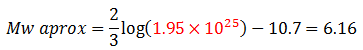
Al contrastar este valor, con la magnitud de momento reportada según Suarez (1990) de “Mw=6.4”, podemos establecer una diferencia porcentual de la siguiente forma:
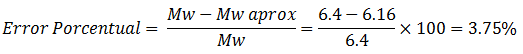
Una diferencia porcentual que se puede disminuir probando con el rango de valores de longitud, ancho y desplazamiento dados a lo largo de las inecuaciones N°02, N°03 y N°04.
Caso N°02: sismo de Cariaco, edo. Sucre, año: 1997. Mw=6.9, profundidad al foco de 9.6 km
Este evento sísmico afectó las zonas de Cariaco y Cumaná. La longitud de la traza de la falla afloró en la superficie. Fue un sismo de foco superficial, cuya falla causante es de tipo transcurrente; todos estos argumentos nos dan base para la aplicación de las ecuaciones de Wells y Coppersmith. La metodología de cálculo es en esencia la misma a la del caso N°01, solo tenemos que variar la magnitud de momento “Mw” y estar atentos de aplicar la ecuación de longitud de ruptura superficial “SRL”. A continuación presento una tabla resumen de los resultados y en la imagen N°07 una ilustración didáctica de los mismos:
Tabla N°01: resumen de resultados obtenidos de la aplicación de las fórmulas de Wells y Coppersmith

Fuente:@eliaschess333, año: 2018.
Imagen N°07: resumen de parámetros geométricos del plano de falla, para el caso de estudio N°02
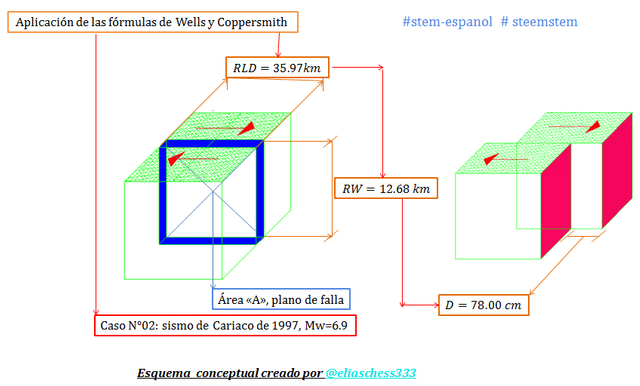
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint, Paint y AutoCAD 2007.
Basados en el esquema conceptual de la imagen N°07, el área de ruptura “A” viene dada por:
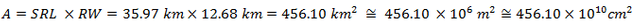
Conociendo el área de ruptura “A” calculamos el momento sísmico “Mo”:
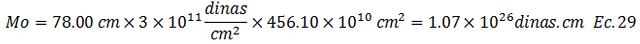
Estimamos la magnitud de momento aproximada “Mw aprox”, aplicando la ecuación N°01, y utilizando el momento sísmico “Mo” en unidades de “dinas.cm”, obtenido con los datos del plano de ruptura que arrojan las relaciones de Wells y Cooppersmith:
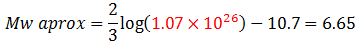
Al contrastar este valor, con la magnitud de momento reportada según archivo de FUNVISIS (ref. 06) de “Mw=6.9”, podemos establecer una diferencia porcentual de la siguiente forma:
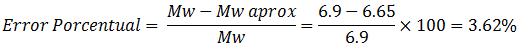
Una diferencia porcentual que se puede disminuir probando con el rango de valores de longitud, ancho y desplazamiento dados a lo largo de las inecuaciones presentadas en la tabla N°01.
CONCLUSIONES
La magnitud “Mw” de un sismo como medida cuantitativa del tamaño del mismo, podemos utilizarla para hacernos una idea de lo grande que resultan los planos de fallas donde la roca más rígida de la litosfera, experimenta la superación de su límite elástico, con la consecuencia inmediata de la liberación de energía potencial. En este trabajo, los cálculos fueron ajustados a las sismicidad venezolana, tomando como referencia los dos sismos más importantes que en el país han ocurrido. Entre las conclusiones de mayor importancia que se derivan de este trabajo tenemos las siguientes:
1.- La magnitud de momento “Mw” está influenciada directamente por el tamaño del plano de falla.
2.- En términos numéricos la diferencia porcentual entre “Mw” y “Mw aprox”, calculada esta última a partir de los resultados provenientes de las aplicaciones de las fórmulas de Wells y Coppersmith, es pequeña, menor al 5%.
3.-Evidentemente en términos del momento sísmico producido, y de la energía liberada, la diferencia es grande. Por eso es importante recalcar, que la aplicación de las fórmulas de Wells y Coppersmith, ha de hacerse con el adecuado criterio estadístico, es decir, los parámetros geométricos del plano de falla que se obtienen con la aplicación de estas fórmulas, no son valores exactos, de allí a que se establece un rango de valores, haciendo uso de la desviación estándar.
4.- No obstante, es de gran utilidad la aplicación de las fórmulas de Wells y Coppersmith, para hacernos una idea, bastante cercana a la realidad del tamaño del plano de falla.
5.-Es importante resaltar que las fórmulas empleadas, aplican al caso de fallas transcurrentes, aspecto característico de la sismicidad venezolana.
Hasta este punto, hemos profundizado en diversas aplicaciones que podemos hacer conociendo la magnitud “Mw” de un sismo; por lo que es de interés profundizar en los efectos locales de los mismos, abriendo las puertas al concepto de intensidad; aspecto en el cual estaré profundizando en una próxima publicación.
Escribió para ustedes:
FUENTES DE INFORMACIÓN CONSULTADAS
1.- SAUTER F. 1989. FUNDAMENTOS DE LA INGENIERÍA SÍSMICA I: INTRODUCCIÓN A LA SISMOLOGÍA. EDITORIAL TECNOLÓGICA DE COSTA RICA.
2.- TARBUCK E. Y LUTGENS F. 2005. CIENCIAS DE LA TIERRA, UNA INTRODUCCIÓN A LA GEOLOGÍA FÍSICA, OCTAVA EDICIÓN. PEARSON EDUCACIÓN, S.A.
3.- MCGUIRE R. 2004. SEISMIC HAZARD AND RISK ANALYSIS. EARTHQUAKE ENGINEERING RESEARCH INSTITUTE.
4.- WELLS D. AND COPPERSMITH K. 1994. NEW EMPIRICAL RELATIONSHIPS AMONG MAGNITUDE, RUPTURE LENGTH, RUPTURE WIDTH, RUPTURE AREA AND SURFACE DISPLACEMENT. BULLETIN OF THE SEISMOLOGICAL SOCIETY OF AMERICA, VOL. 84, N°4, pp. 974-1002.
5.- SUÁREZ Y NÁBLEK. 1990. THE 1967 CARACAS EARTHQUAKE: FAULT GEOMETRY, DIRECTION OF RUPTURE PROPAGATION AND SEISMOTECTONIC IMPLICATIONS. JOURNAL OF GEOPHYSICAL RESEARCH. VOL. 95, NO.B11. PAGES 17459-17474.
6.- TERREMOTO CARIACO. DISPONIBLE EN: http://www.funvisis.gob.ve/old/reportaje9.php. CONSULTADO EL 21 DE MAYO DEL 2018
LECTURAS RECOMENDADAS
7.- SANTANA E. 2018. ESTUDIO DE LA MAGNITUD DE UN SISMO. UNA VISIÓN PRÁCTICA DE LOS APORTES DE LA SISMOLOGÍA. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/estudio-de-la-magnitud-de-un-sismo-una-vision-practica-de-los-aportes-de-la-sismologia
8.- APLICACIÓN DE LA INTEGRACIÓN DEFINIDA EN EL CÁLCULO DEL TRABAJO REALIZADO POR UNA FUERZA VARIABLE (PERSPECTIVA ANALÍTICA Y NUMÉRICA). DISPONIBLE EN: https://steemit.com/stem-espanol/@ydavgonzalez/aplicacion-de-la-integracion-definida-en-el-calculo-del-trabajo-realizado-por-una-fuerza-variable-perspectiva-analitica-y
Excelente men cada artículos que montas vale la pena leer y compartir , felicidades excelente trabajo
Gracias @gerardoalfred, muy motivador tu comentario para seguir trabajando en la producción de artículos de interés. Saludos!
super interesante.
Saludos @naika gracias por el apoyo!
Saludos, me gusta la calidad técnica de tus artículos. Tiene un aire a lo Capablanca, solo al (la) final se deslumbra todo. ;-)
Saludos @soy-venezuelien, interesante la analogía que haces. Agradecido por el apoyo!
Excelente como siempre @eliaschess333. El post está muy completo. Felicitaciones!
Gracias @xandra79, me complace leer tu comentario. Saludos!
Gracias por el aporte @eliaschess333. Saludos.
Saludos @elvigia gracias a ti por estar al tanto de mis publicaciones!
Excelente material, muy formativo y educativo, éxitos.
Igual para tí @felixrodriguez. Educar más allá de los muros del aula me encanta, y en esta plataforma lo podemos lograr. Saludos!
Lo vi y creo que por lo menos podemos darle un voto. Ayúdame a que este corazón no deje de latir