Simulación de un Sistema Lineal de Segundo Orden Utilizando el Software SciLab
Hola, amigos de Steemit
Después de una ausencia de aproximadamente dos meses, he vuelto para presentarles este artículo básico orientado al fascinante mundo de las simulaciones de los "Sistemas de Control Lineal e Invariantes en el Tiempo". Las simulaciones fueron realizadas con ayuda del programa SciLab (software libre, versión 5.4.1) utilizando la librería interna del simulador XCOS para la construcción de los Diagramas de Control (DDC). Se muestran las gráficas de las respuestas del sistema a las señales de entrada tipo escalón unitario y tipo rampa unitaria. ¡Sean todos bienvenidos!

Se entiende por "respuesta forzada de un sistema" a la respuesta que depende de las señales de entrada, y se obtiene cuando las condiciones iniciales x(0) se asumen iguales a cero. En este documento supondremos que el sistema es excitado con una señal de entrada u(t) y se obtendrá la respuesta forzada y(t). En otras palabras, la idea se centra en en hallar las respuestas forzadas de un sistema lineal, continuo e invariante en el tiempo cuando, por separado, lo excitemos con una señal tipo "escalón unitario" y luego con una señal tipo "rampa unitaria". El propósito no es otro que ilustrar cómo ese mismo sistema responde de manera distinta (comportamiento gráfico) ante dos señales diferentes y que los resultados obtenidos sirvan de base para que el lector pueda redactar sus propias conclusiones y observaciones. En adelante, usaremos las siglas “EDO” para referirnos a una "Ecuación Diferencial Ordinaria".

Supongamos que la EDO que se indica a continuación representa a un sistema continuo, lineal e invariante en el tiempo. Nota: Asuma que las condiciones iniciales son todas iguales a cero.

Donde:
u(t) : Señal de entrada.
y(t) : Señal de salida.
Para tener una idea más clara, veamos la siguiente figura:

Observación:
- SISO: siglas en inglés de “Single Input/Single Output (una entrada/una salida).

Representación matemática:
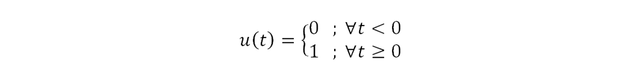
Representación grafica:
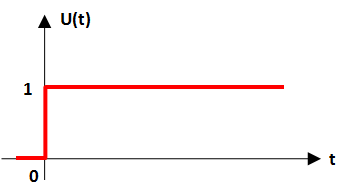
Señal escalón unitario con desplazamiento temporal
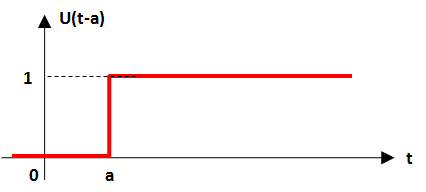
Al desplazar la señal anterior en el eje del tiempo, resulta lo siguiente:
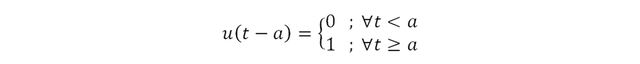
Representación grafica:

Representación matemática:
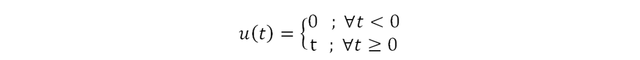
Vemos que se trata de la ecuación de una recta con pendiente m=1 (∀t ≥ 0).
Representación grafica:
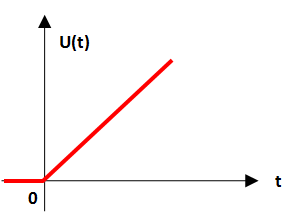
Señal rampa unitaria con desplazamiento temporal
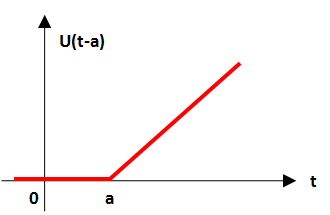
Al desplazar la señal anterior en el eje del tiempo, resulta lo siguiente:
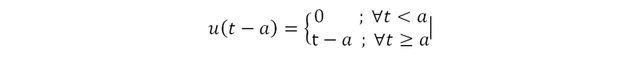
Representación grafica:
Respuesta Escalón
Ahora procedemos a excitar el sistema con la señal escalón unitario para observar cómo es su respuesta.
Para elaborar el DDC de una ecuación diferencial se despeja la derivada de mayor orden; en este caso tenemos una EDO de segundo orden (n = 2); por lo tanto, despejamos la segunda derivada en la Ec(1):
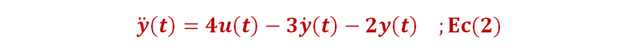
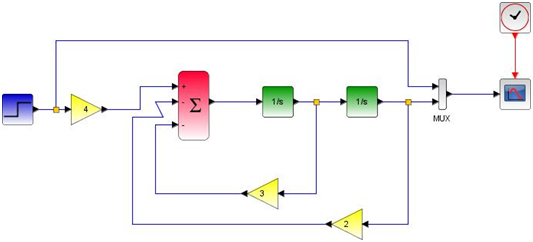
Diagrama de control con entrada escalón unitario:
A partir de la Ec(2) se obtiene el siguiente DDC haciendo uso del simulador XCOS del software SciLab.
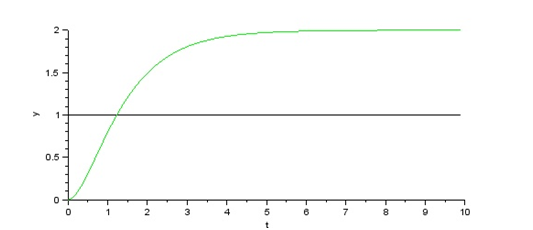
Respuesta a la señal escalón unitario:
La siguiente gráfica muestra que para el instante t=0, se activa la señal u(t) y el sistema responde con una señal y(t) continua y creciente en el tiempo. La respuesta tiende a estabilizarse a un valor final Yf ≈ 2 unidades. Podemos afirmar, para este caso en particular, que el sistema responde de manera ESTABLE ante una señal de entrada tipo “Escalón Unitario”.
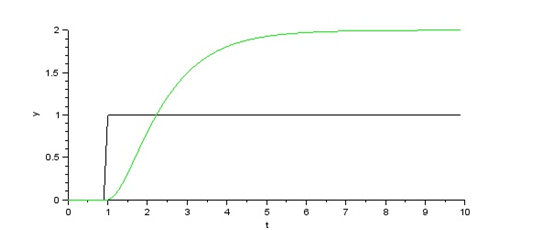
Respuesta a la señal escalón unitario con desplazamiento en el tiempo:
Supongamos que desplazamos la señal escalón en el eje del tiempo, en un valor: a = 1. Se observa que la respuesta del sistema es cero hasta el instante t = 1s. A partir de ese momento se activa u(t) y el sistema responde con una señal y(t) continua y creciente en el tiempo hasta estabilizarse en el valor final Yf ≈ 2 unidades.
Respuesta Rampa
¿Cómo responde ese mismo sistema si lo excitamos con una señal tipo rampa unitaria? Es obvio pensar que la respuesta debería ser diferente como, de facto, lo es; pero no basta decirlo. Por lo tanto, hagamos la prueba a ver qué resulta.
Diagrama de control con entrada rampa unitaria:
En el DDC del caso anterior solamente cambiamos el tipo de fuente que alimentará al sistema; es decir, la señal escalón la cambiamos por la señal rampa.

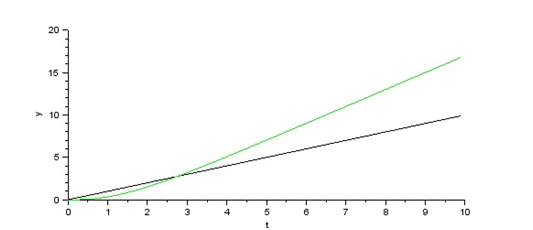
Respuesta a la señal rampa unitaria:
Observamos que la respuesta del sistema crece indefinidamente; por lo tanto, podemos afirmar que el sistema se comporta de manera INESTABLE.
Respuesta a la señal rampa unitaria con desplazamiento en el tiempo:
Sugerencia: se deja como ejercicio simular la respuesta del sistema suponiendo que la entrada es una señal rampa unitaria desplazada en el tiempo .

En relación a la EDO del ejemplo anterior, responda las siguientes preguntas con criterios de ingeniería y justifique analíticamente su respuesta de ser necesario:
- ¿Por qué decimos que el sistema es continuo?
- ¿Por qué decimos que el sistema es lineal?
- ¿Por qué decimos que el sistema es invariante en el tiempo?
- Aplicar el teorema del Valor Final para obtener analíticamente el valor de la señal en régimen estable.
- ¿Qué nombre recibe la respuesta del sistema cuando no hay señal de entrada; es decir, para u(t)=0? ¿Tiene sentido físico hablar de respuesta del sistema bajo tal condición?
- Simular la respuesta o comportamiento del sistema cuando u(t)=0. Sugerencias: (a) Escribir la ecuación diferencial resultante. (b) Elaborar el DDC. (c) Obtener la gráfica de la respuesta del sistema. (d) Analizar el resultado.
- Aplicar la Transformada de Laplace (TDL) para encontrar: (a) La función de transferencia (FDT) del sistema. (b) El polinomio característico. (c) Los polos.
- Determinar los ceros finitos y ceros en el infinito, si existen.

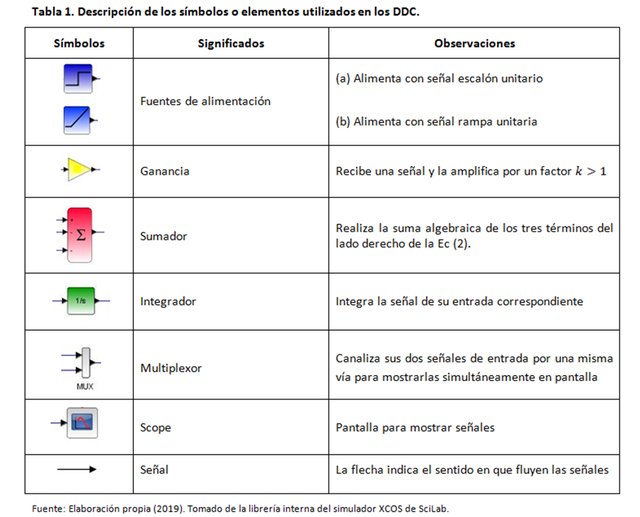
A objeto de facilitar la comprensión de los DDC se muestra la siguiente Tabla con el significado de todos los símbolos utilizados, los cuales forman parte de la librería interna del simulador XCOS.

REFLEXIÓN


Hello @reyito! This is a friendly reminder that you have 3000 Partiko Points unclaimed in your Partiko account!
Partiko is a fast and beautiful mobile app for Steem, and it’s the most popular Steem mobile app out there! Download Partiko using the link below and login using SteemConnect to claim your 3000 Partiko points! You can easily convert them into Steem token!
https://partiko.app/referral/partiko
Congratulations @reyito! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking