
¡Hola amigos de Steemit, grato saludarles!
En este documento les mostraré a través de un ejercicio cómo obtener la función de transferencia G(S) de un sistema de control lineal mediante la fórmula de Mason. La referida fórmula resulta de gran utilidad en el estudio de los sistemas de control cualquiera sea la disciplina (eléctrica, electrónica, mecánica, sistemas, entre otras) o la naturaleza del problema a abordar. El ejercicio desarrollado en este artículo lo tomé de una de mis clases impartidas a los estudiantes de ingeniería, específicamente en la asignatura SISTEMAS. Se basa en un sistema de control lineal con una señal de entrada y una señal de salida (SISO: "Single Input/Single Output"). Iniciaremos la temática con la simple definición de lo que es una función de transferencia, veremos el concepto de lo que es un "diagrama de bloques", y en qué consiste un “diagrama de flujo de señales", para finalmente presentar la fórmula de Mason y su aplicación. Espero que esta exposición sea de mucha utilidad para aquellas personas que están familiarizadas con el referido tema; y a quienes no han tenido la oportunidad de interactuar con este maravilloso y fascinante campo del saber, los invito a tratar de comprender el contenido. Sean todos(as) bienvenidos(as).

Ogata (1989), sostiene que en el campo de la teoría de los sistemas, las funciones de transferencia “(…) se usan frecuentemente para caracterizar las relaciones de entrada y salida de sistemas de ecuaciones diferenciales lineales, invariantes en el tiempo (…) y se define como la relación de la transformada de Laplace de la salida (función de respuesta) y la transformada de Laplace de la entrada (función impulsora o de excitación) bajo la suposición de que todas las condiciones iniciales sean cero” (p.389).
De acuerdo con lo anterior, la función de transferencia G(S) de un sistema de control es una expresión matemática que permite conocer la relación entre la señal de entrada X(S) y la señal de salida Y(S), tal como se muestra en la Figura 1.
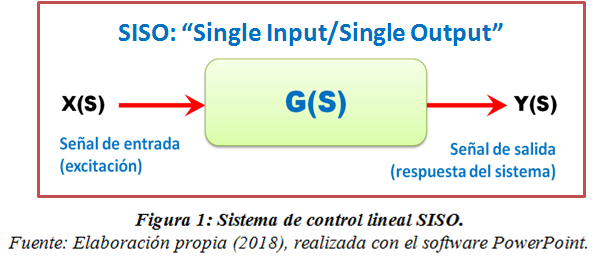
Por lo tanto:
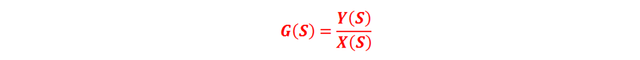
Donde: X(S), Y(S) y G(S) corresponden a las transformadas de Laplace de las funciones en el dominio del tiempo x(t), y(t) y g(t), respectivamente. Es importante volver a acotar que el cálculo de una función de transferencia (FDT) supone que las condiciones iniciales sean iguales a cero. Por otro lado, vale recordar que la variable “S” pertenece al campo de los números complejos; en este caso S=jω, donde
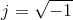
(unidad imaginaria) y
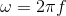
(frecuencia angular en rad/s con f = frecuencia oscilatoria en Hz). En general, la variable compleja “S” viene dada por
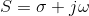
, pero para el cálculo de las FDT se considera cero el factor de atenuación (σ = 0). Dado que el alcance de este documento es meramente presentar la fórmula de Mason (FDM), no viene al caso profundizar en las razones que conllevan a considerar como nulo el efecto de atenuación de las señales, lo cual se deja a discreción del lector y su inquietud de querer hurgar sobre el tema.
Tipos de señales de entrada comúnmente utilizadas:
- Señal de impulso (Delta de Dirac):
)
- Señal escalón unitario:
)
- Señal rampa unitaria:
)
- Señal senoidal:
)

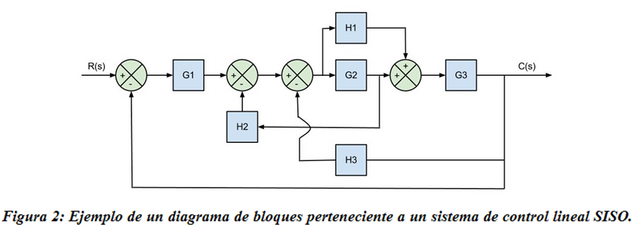
De acuerdo con Ogata (1998), un diagrama de bloques (DDB) de un sistema “es una representación gráfica de las funciones realizadas por cada componente y del flujo de las señales (…) y describe las interrelaciones que existen entre los diferentes componentes. Las FDT de los componentes usualmente se meten en los bloques correspondientes” (p.497). Dicho de otra manera, un DDB contiene flechas que indican la dirección en que fluyen las señales que tienen que intervienen en el sistema (señales de entrada, señales de salida, señales internas, perturbaciones), y rectángulos (bloques) los cuales representan las partes de un sistema o proceso (planta, controladores, actuadores, realimentación, entre otros) concebidos como una “caja negra” en cuyo interior están presentes las características intrínsecas que dan lugar a funciones de transferencias (ganancias) de cada bloque, y que de una manera u otra influirán en el comportamiento global del sistema original. Cuando los parámetros internos de los bloques son constantes se generan ecuaciones diferenciales con coeficientes que también son constantes lo que significa que el sistema es invariante en el tiempo, en otras palabras, las propiedades internas del sistema permanecen intactas ante la acción del tiempo; en caso contrario estaríamos hablando de un sistema variante en el tiempo; trataremos el primero de los casos. La Figura 2, muestra un ejemplo de un DDB.
 Fuente
Fuente
En la Figura 2, las H corresponden a las ganancias de los lazos de realimentación, mientras que las G corresponden a las ganancias de los lazos directos. Los círculos representan SUMADORES, los cuales reciben o admiten varias señales de entrada y generan una salida que es la suma algebraica de sus correspondientes entradas.

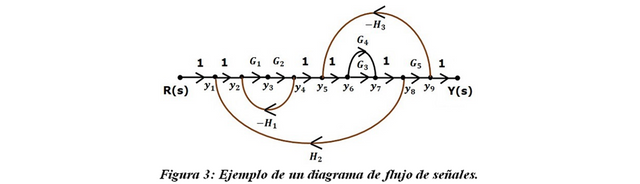
El diagrama de flujo de señal (DFS) se obtiene a partir del DDB; es decir, puede ser visto como una versión simplificada de un DDB. Un ejemplo se muestra en la Figura 3.
 Fuente
Fuente
Propiedades de los DFS:
Las más comunes son:
- Simplificación de Ganancias en Serie.
- Simplificación de Ganancias en Paralelo.
- Eliminación de Nodos Internos.
- Eliminación de Lazos.

La ganancia total G(S) de un DFS, entre el nodo de entrada y el de salida y que contiene varias trayectorias directas, está determinada por la siguiente ecuación:
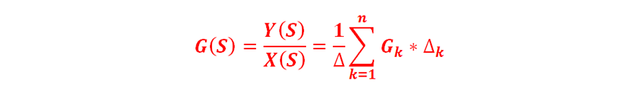
Desarrollando la sumatoria, resulta:
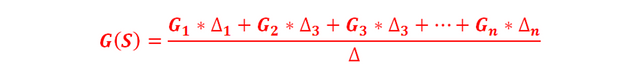
Donde:
- ∆ : Determinante del DFS (gráfico completo) y se determina mediante la fórmula:
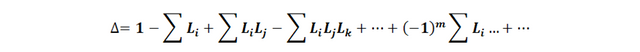
- X(S) : Variable de entrada (representa a la señal de entrada).
- Y(S) : Variable de salida (representa a la señal de salida).
- G(S) : Ganancia o FDT del sistema completo entre Y(S) y X(S).
- n : Número de caminos (trayectorias) directos posibles entre Y(S) y X(S).
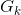 : Ganancia en la trayectoria k-ésima desde el nodo de entrada hasta el nodo de salida y la cual es igual al producto de las ganancias de las ramas que componen la trayectoria.
: Ganancia en la trayectoria k-ésima desde el nodo de entrada hasta el nodo de salida y la cual es igual al producto de las ganancias de las ramas que componen la trayectoria.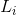 : Ganancia de todos los lazos simples.
: Ganancia de todos los lazos simples.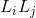 : Producto de las ganancias de lazos disjuntos tomados de dos en dos.
: Producto de las ganancias de lazos disjuntos tomados de dos en dos.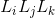 : Producto de las ganancias de lazos disjuntos tomados de tres en tres.
: Producto de las ganancias de lazos disjuntos tomados de tres en tres.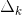 : Es el cofactor de
: Es el cofactor de 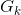 , es decir, el determinante del sub-gráfico que queda cuando se remueve (se quita) la trayectoria
, es decir, el determinante del sub-gráfico que queda cuando se remueve (se quita) la trayectoria 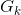 . (Nota:
. (Nota: 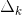 se define de la misma forma que el determinante ∆ del DFS, solo que las ganancias sustituidas en las fórmulas corresponden a los lazos que no tocan a la trayectoria k-ésima directa).
se define de la misma forma que el determinante ∆ del DFS, solo que las ganancias sustituidas en las fórmulas corresponden a los lazos que no tocan a la trayectoria k-ésima directa).

Obtener la función de transferencia G(S) de un sistema de control cuyo diagrama de bloques se muestra en la siguiente figura, aplicando la fórmula de Mason.
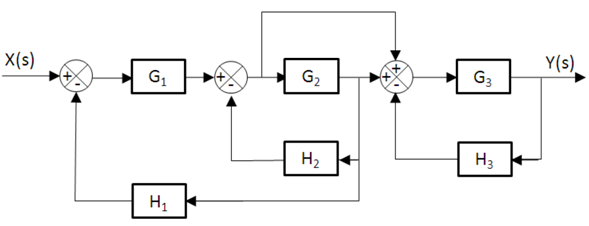
SOLUCIÓN
Paso #1: Construcción del DFS.
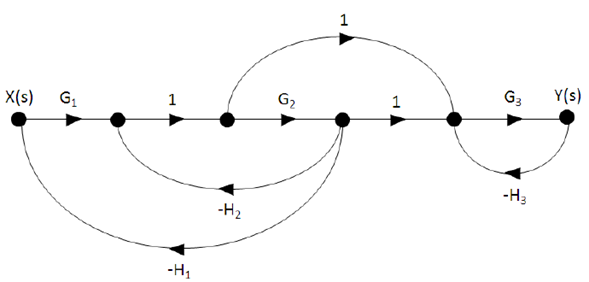
Paso #2: Identificación de los caminos directos.
- Existen dos caminos directos (n = 2) identificados con el color rojo en el siguiente diagrama.
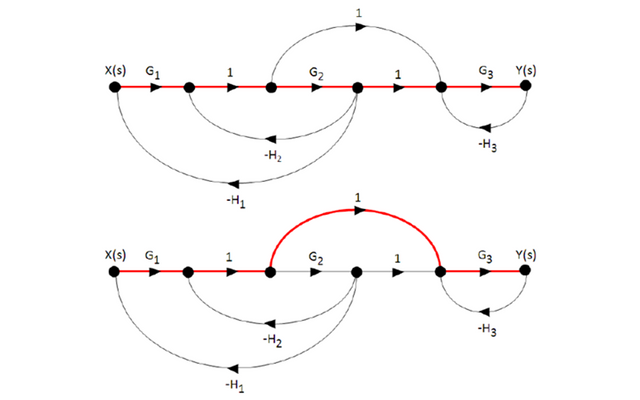
- Fórmula de Mason para n = 2:
\:&space;\:&space;\:&space;\:&space;\:&space;G\left&space;(&space;S&space;\right&space;)=\frac{1}{\Delta&space;}\sum_{k=1}^{2}G_{k}\Delta&space;_{k}=\frac{G_{1}\Delta&space;_{1}+G_{2}\Delta&space;_{2}}{\Delta&space;})
De acuerdo con (I) debemos hallar las ganancias de los caminos directos (
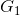
y
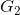
), el determinante (∆) y los cofactores (
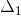
y
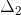
) .
Paso #3: Determinación de las ganancias de los caminos directos.
Para k=1: 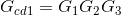 (II)
(II)
Para k=2:  (III)
(III)
Paso #4: Identificación de todos los lazos o bucles del sistema
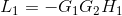 (IV)
(IV)
 (V)
(V)
 (VI)
(VI)
Paso #5: Determinación del determinante ∆
Sabemos que :
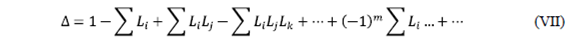
- Sumatoria de todas las ganancias de los lazos:
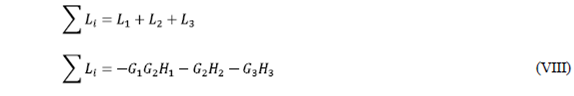
- Sumatoria de las ganancias de lazos disjuntos tomados de dos en dos:
En el DFS se observa lo siguiente:
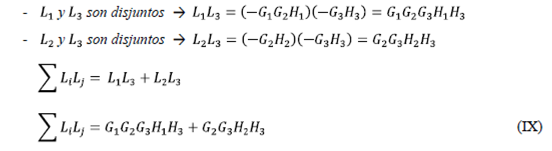
- Sumatoria de las ganancias de lazos disjuntos tomados de tres en tres:
¡En el DFS se observa que NO EXISTEN!
Sustituimos (VIII) y (IX) en (VII):
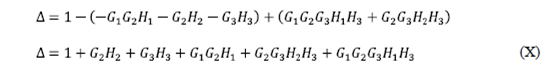
Paso #6: Determinación del cofactor 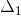
- Debemos remover (quitar) del DFS el camino directo
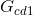 , y al gráfico resultante se le aplican los mismos criterios para el cálculo de ∆ (véase la siguiente figura).
, y al gráfico resultante se le aplican los mismos criterios para el cálculo de ∆ (véase la siguiente figura).
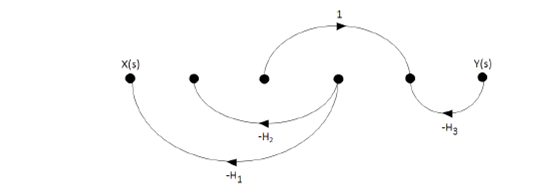
Sumatoria de todas las ganancias de los lazos:
No existen lazos, por lo tanto el resultado es CERO.
Sumatoria de las ganancias de lazos disjuntos tomados de dos en dos:
No existen lazos disjuntos, por lo tanto el resultado es CERO.
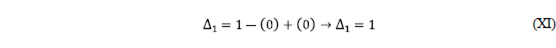
Paso #7: Determinación del cofactor 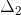
- Debemos remover (quitar) del DFS el camino directo
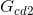 , y al gráfico resultante se le aplican los mismos criterios para el cálculo de ∆ (véase la siguiente figura).
, y al gráfico resultante se le aplican los mismos criterios para el cálculo de ∆ (véase la siguiente figura).
Sumatoria de todas las ganancias de los lazos:
No existen lazos, por lo tanto el resultado es CERO.
Sumatoria de las ganancias de lazos disjuntos tomados de dos en dos:
No existen lazos disjuntos, por lo tanto el resultado es CERO.
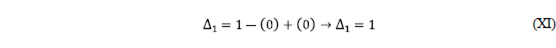
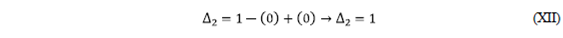
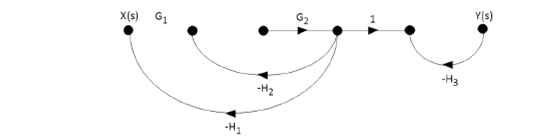
Paso #8: Determinación de la función de transferencia del sistema de control .
Sustituimos (II), (III), (X), (XI) y (XII) en (I).

CONCLUSIONES
A pesar de que el método resulta, EN APARIENCIA, un tanto engorroso, paradójicamente es relativamente fácil de entender y de aplicar, y considero oportuno concluir dando respuesta a una pregunta de mucha importancia:

La respuesta es muy sencilla: Lo hacemos porque, en general, la mayoría de los sistemas de control reales presentan un elevado nivel de complejidad dada la cantidad de lazos de interconexión y lazos de realimentación que lo conforman, lo cual dificulta enormemente la obtención de G(S) por los métodos de simplificación matemática que comúnmente conocemos, resultando tendenciosamente mayor el riesgo a equivocarnos. En cambio, la probabilidad de cometer errores es mucho menor al aplicar la FDM por cuanto nos ahorramos los pasos intermedios del método tradicional.
Una vez conocida la función de transferencia, ésta puede ser utilizada para llevar a cabo estudios posteriores relativos a la ESTABILIDAD del sistema de control a partir de la ubicación de los polos en el plano complejo, los cuales se obtienen del polinomio característico.
Se puede verificar de manera gráfica las formas cómo varían tanto la magnitud como el ángulo de la función de transferencia con la frecuencia (Diagramas de Bode), y de este modo precisar el rango o gama de frecuencias para la cual se observa un comportamiento determinado en la respuesta gráfica del sistema.
REFERENCIA




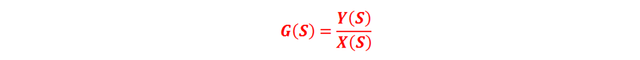



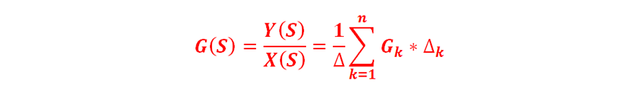
: Ganancia en la trayectoria k-ésima desde el nodo de entrada hasta el nodo de salida y la cual es igual al producto de las ganancias de las ramas que componen la trayectoria.
: Ganancia de todos los lazos simples.
: Producto de las ganancias de lazos disjuntos tomados de dos en dos.
: Producto de las ganancias de lazos disjuntos tomados de tres en tres.
: Es el cofactor de
, es decir, el determinante del sub-gráfico que queda cuando se remueve (se quita) la trayectoria
. (Nota:
se define de la misma forma que el determinante ∆ del DFS, solo que las ganancias sustituidas en las fórmulas corresponden a los lazos que no tocan a la trayectoria k-ésima directa).



(II)
(III)
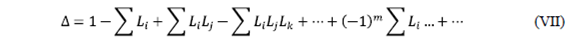
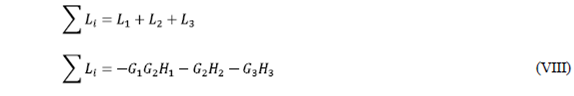
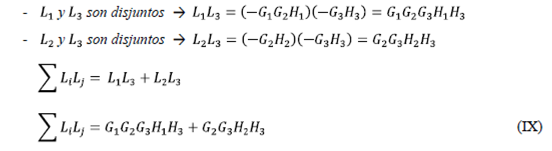
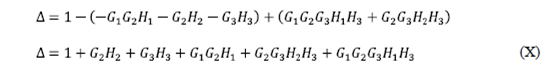
, y al gráfico resultante se le aplican los mismos criterios para el cálculo de ∆ (véase la siguiente figura).

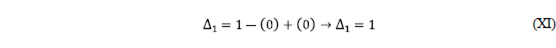
, y al gráfico resultante se le aplican los mismos criterios para el cálculo de ∆ (véase la siguiente figura).

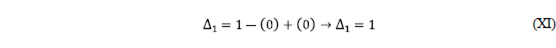
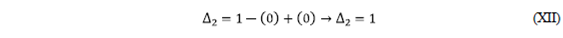




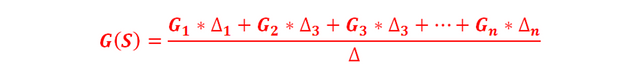
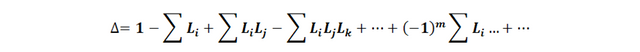


As a follower of @followforupvotes this post has been randomly selected and upvoted! Enjoy your upvote and have a great day!
Thank you for selecting and voting my article. I also want to thank you for wishing me a good day. May God shower his blessings on all people.