Probing the Heart of Quantum Mechanics: Operators and Schrodinger Equation

the heart of quantum mechanics
Observables and Operators
In quantum mechanics it has been a practice that for every measurable quantity A, often called an observable, we can associate an operator 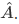 If a particle is in a state with a definite value a of A then,
If a particle is in a state with a definite value a of A then,
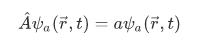
This kind of transformation, where the action of the operator 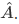 on the wavefunction results to the wavefunction itself times some scaling value a is known as an eigenvalue problem. We can name the players of this problem as such,
on the wavefunction results to the wavefunction itself times some scaling value a is known as an eigenvalue problem. We can name the players of this problem as such,
Example of Operators
From previous discussion about definite energy and momentum, we where able to obtain a wavefunction of the form,
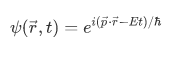
Consider the idea that for each observable there is an associated operator 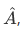 , then we should have an operator, let's say,
, then we should have an operator, let's say, 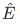 for the observable E, and equivalently an operator
for the observable E, and equivalently an operator 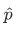 for the observable p. Using the eigenvalue equation:
for the observable p. Using the eigenvalue equation:
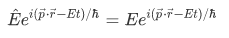
and
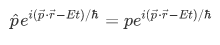
Now, what we need to know is determine the appropriate form of the operators to satisfy the eigenvalue problem.
First, lets consider the wave function and take its partial derivative with respect to time,
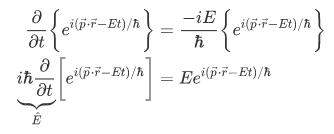
We can see clearly that the operator 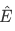 is given by
is given by
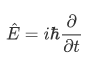
For the momentum eigenvalue problem, one can determine by expressing the momentum and position in terms of its component 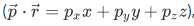 , that the operator
, that the operator 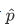 is given by,
is given by,
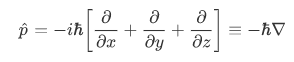
We can also find the position operator by considering a wave function corresponding to definite position. We restrict ourselves, for the moment, to motion confined to one dimension. A particle with a definite position 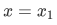 will be described by a wave function with the following spatial dependence:
will be described by a wave function with the following spatial dependence:
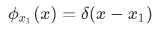
The delta is a function 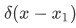 that dictates whether the particle is on the definite position of
that dictates whether the particle is on the definite position of 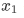 or not. Consider for instance, if
or not. Consider for instance, if 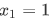 , if it happens that our
, if it happens that our 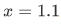 , then we have,
, then we have,
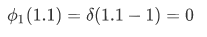
using the definition of Dirac-delta function.
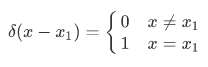
Similar to the previous example of operators, we need an operator 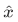 for the observable x, that will satisfy the following transformation:
for the observable x, that will satisfy the following transformation:
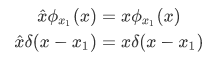
Clearly, the multiplicative nature of the position satisfy the required property, so for position operator it is defined by,
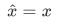
One can also have a similar operator for 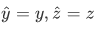 or generalize to the three-dimensional position,
or generalize to the three-dimensional position,
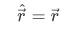
Using our derived operators, we can create the corresponding general observable 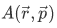 by using the following prescription,
by using the following prescription,
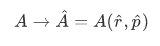
where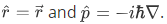 Lets consider the following observables common in classical mechanics,
Lets consider the following observables common in classical mechanics,
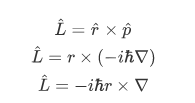
Summary:
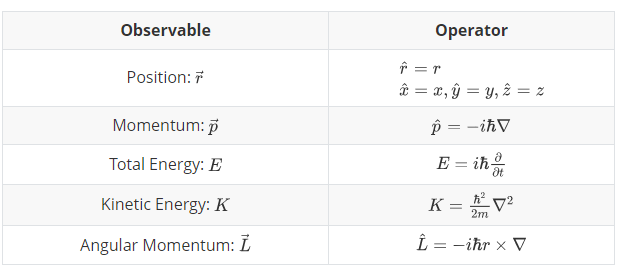
The Time-Dependent Schrodinger Equation
From classical mechanics, we know that the total energy of a particle is given by the sum of the kinetic energy and potential energy.
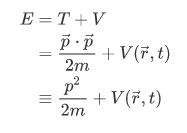
We then replace this equation with its equivalent operator:
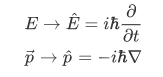
So, substituting these equations to the total energy equation, we have:
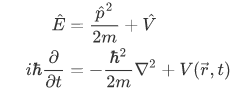
A physically acceptable wave function 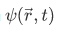 must satisfy the equation,
must satisfy the equation,
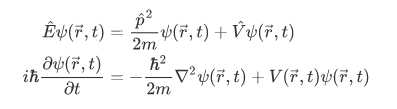
This is known as the time-dependent Schrodinger equation, and is a completely general differential equation for the evolution of the wave function 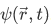 .
.
That's it.
We know now the differential equation that will dictate the dynamics of our state (wave function). This is all we need to make sense of all quantum systems that are non-relativistic.
Memorize this equation for this is the working tool of quantum mechanics.
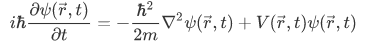
Credit
- all equations are generated using Sharelatex
- the first image is obtain from Pixabay under CC0 Creative Commons
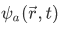
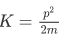
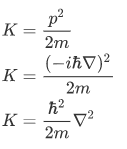
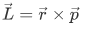
You got a 4.87% upvote from @minnowvotes courtesy of @pauldirac!
Your posts are of great value to students in quantum mechanics.
Thanks for all the work.
That's good to hear.