Greetings everyone, respected steem users

Before starting to explain the topic of this publication, I want to mention that I am just a common user who tries to share in the best possible way the content related to the #STEM areas, taking advantage of the opportunity offered by the blockchain and the community Respected by @steemstem to publish topics related to science from an entertaining and inclusive perspective for all, members of the ste and interested community, therefore, the themes presented represent a particular understanding of the basic lessons, but they are important for the domain of knowledge in general. I just hope you like my job

In this opportunity we will talk about the determinants, an algebraic technique related to the solutions to systems of linear and first-degree equations, something super basic that are part of the mathematics lessons in high school and in addition to easy compression, then consider the following system:

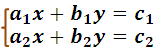
Remember that, in general, the solution to this system can be obtained by means of the methods of substitution, elimination, equalization or any type of mathematical device so that we can obtain:

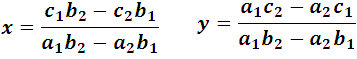
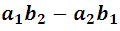
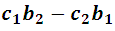
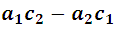
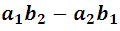
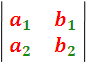
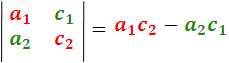
Note that the denominator is common for both variables and it is obvious that it must be different from 0. Now, the differences between the products: , y that appear in the solutions, we can obtain it easily, if we adopt a symbol, and we establish that:

It is represented by the symbol which is called

, because it consists of four elements and arranged in two rows and in two columns. The elements a₁ and b₂ it is said that they form the principal diagonal of the determinant and represents the first product, then the other two elements complements the expression. In summary, according to what is established, it follows that:

And this difference expresses the value or development of the determinant. In a similar way:

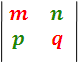
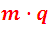
They form two other determinants of 2⁰ order. In a general way, the symbol , represents the difference between the products and , that is, its diagonals.

Properties of the second order determinants.

In second order determinants we can notice, among others, the following properties:

• The value of a second-order determinant does not alter if the rows are combined by columns. So:

because both are equal to .

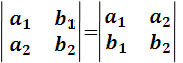
• Permuting the two rows or the two columns between them, the determinant changes its sign, but not its absolute value.

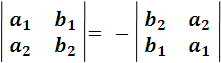
in fact:

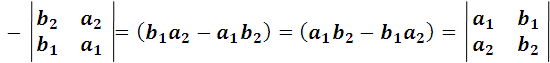
• If the two rows or the two columns are identical, the determinant is null.

So

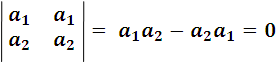
Resolution of systems of equations by determinants

As we already mentioned, the determinants of the second order can be applied in the resolution of a system of two linear equations with two unknowns. In fact, in the general form of these systems we find that:

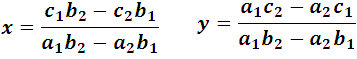
Values that with the determinants very well we can express it in the following way:

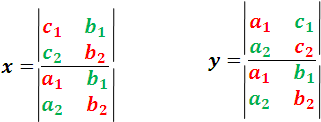
being the common denominator different from zero, these last expressions are also known as formulas ofCrámer (Gabriel Crámer, mathematician of Geneva, 1704-1752). These formulas are easy to apply if you take into account that both fractions have the same denominator, which is a determinant formed by the coefficients of the unknowns previously arranged in their natural order; and the determinant of the numerator of each of said fractions results from replacing in the common determinant of the denominator the column of the coefficients of the unknown that is to be calculated by that of the independent terms.

For example, let's try to solve the following system:

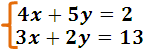
Applying the exposed, it results:

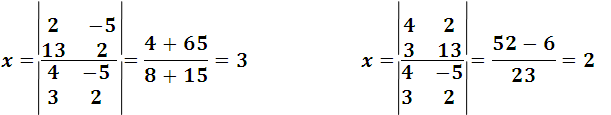
Without a doubt, it is much more practical to solve these problems through the determinants, and are most useful when solving systems of third order equations, as we show you below.

Determinants of third order

Consider the following system:

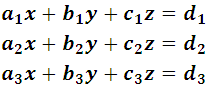
Trying to solve this system by the algebraic methods of equalization or substitution requires in them many algebraic steps, therefore, it is feasible to use the determinants and see how development is. The determinant that appears as a common denominator is represented by the notation:

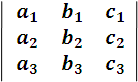
and in an analogous way we can represent the other determinants that appear in the numerators. Proceeding in this way the solution of the system we can express it like this:

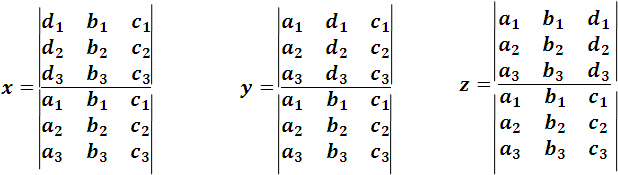
We can notice that in the same way as in a system of two equations with two unknowns, in the common denominator appears the determinant formed with the coefficients of the unknowns previously arranged in their natural order, and the determinants contained in the numerators are formed by substituting the column of the coefficients of the unknown which is calculated by the column of the independent terms.

To obtain the development, we can go to the following diagram, in which, for better understanding, we mark with points the places occupied by the different elements of the indicated determinant:

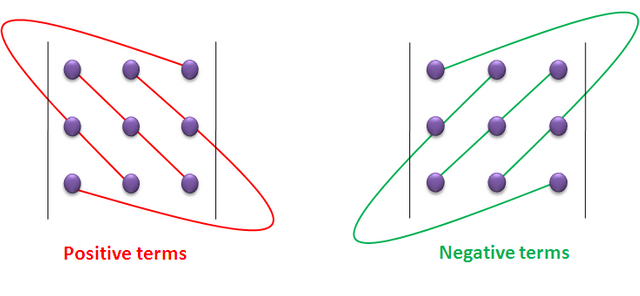
It can be seen that the principal diagonal and its parallels, each of these last with the opposite vertex element, they form the ** positive terms **, and the other diagonal and its parallels, each of these last with the respective opposite vertex element, the negative terms. This rule to express the solutions of linear systems is called the Crámer rule, In short, the determinant of third order is all expression of the form:

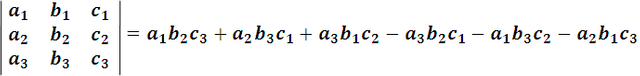
To see an example, let's solve the following system:

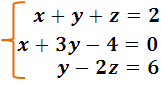
We begin by ordering the system in its natural form and it results:

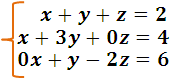
Now we apply the Crámer rule we have:

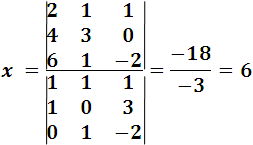
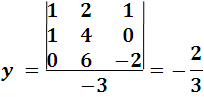
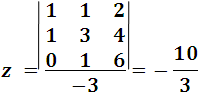
In this way it is demonstrated how easy, practical and useful the determinants to solve problems with respect to systems of linear equations of the first order. Later I will be sharing other points regarding the determinants and generalities about matrices.

For more information regarding the subject you can consult the following ** references **:

• 1
• 2
• 3
• 4

See you later steemians

by @juancmz