Understanding Current in the Subatomic Level

Introduction

     Electric current I is defined as the magnitude of charge passing through a point or surface area per unit second. The unit of a current is the ampere (A) which is equal to coulombs per second (C/s). Current density J, on the other hand, is the amount of electric current flowing per unit cross-sectional area.

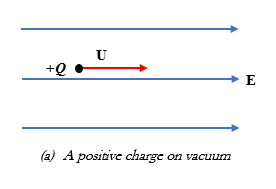
(a) At vacuum, the charge has a clear path and it will continue to accelerate, increasing in velocity U, in the direction of the electric field.

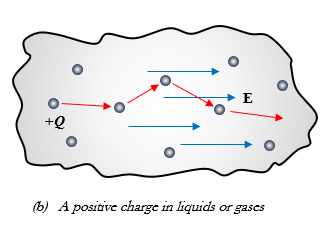
(b) When a charge travels through liquid or gas, the charge would constantly bump the particles on the medium, resulting in random change in direction.

The drift velocity U is directly proportional to the Electric field intensity E, U = μE , where μ the mobility has the units m²/V•s. At higher temperatures, the resistivity of a material increases, thus causing a reduction in mobility.

Convection Current J

     We have learned from our physics that convection occurs with either a liquid or a gas as medium. Let us assume a pack of charged particles, resembling a cloud, moving to the right with velocity U and passing through a surface S.

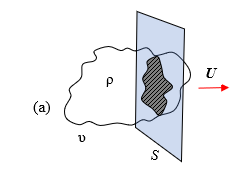
As the pack of charges move through the surface, assuming the particles maintain their relative positions, we can conjure an image of a drifting cloud in the sky. As this cloud of charges υ pass through the surface area, a convection current is formed with density J= ρU (A/m²).

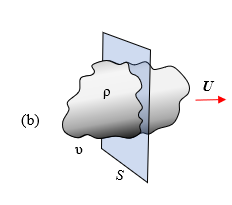
The cross sectional area of the volume υ at a particular time is shown on the figure on the right as the shaded part. We know that while drifting through the surface, this cross section would vary. Therefore we can say that the cross section is not constant but is varying with respect to time. If the charge density is not equally distributed throughout the cloud volume, then we could also say that the charge density ρ would also vary with respect to time.
The current density J of the volume would then be zero as the last portion of the volume crosses the surface S.

Conduction Current J

     Conduction current occurs in the presence of an electric field within a conductor of fixed cross section. Recall from Physics that conduction usually has solids as its medium.

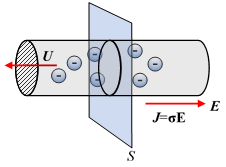
The current density is given by J= ρU (A/m2); and can also be expressed as J=σΕ using the conductivity of the material σ= ρμ in Siemens per meter S/m. Metallic conductors have electrons as charge carriers. Recall that a positive charge has its electric field intensity emanating radially outwards. Hence, an electron would drift in the direction opposite to the electric field.

Conductivity σ

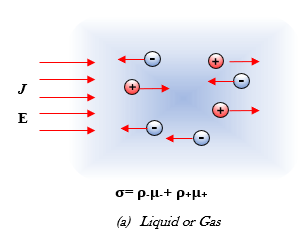
Assuming all the negative ions are alike and all positive ions are alike, the conductivity σ contains two terms. In a liquid or gas, both negative and positive ions are present. The electrons move in the direction opposite to the electric field while the protons move along the direction of the electric field.

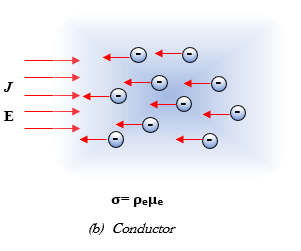
A conductor contains electrons as charge carriers. In a metallic conductor, only the valence electron are free to move. The electrons are moving in the direction opposite to the electric field. The conductivity contains only one term, the product of the charge density of the electrons free to move, ρ_e, and their mobility, μ_e.

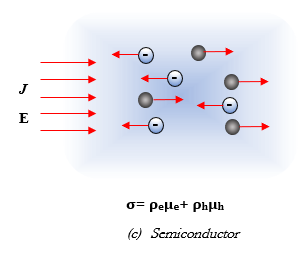
In semiconductors, as an electron moves leftwards, a hole appears from its previous place. The hole is then filled up by another electron in a process called combination. The conductivity σ here consists of two terms, one for the electrons and another for the holes.

Current I

When a current density J crosses a surface S, the current I is obtained by integrating the dot product of J and S.

At uniform current distribution current would simply be equal to I =J S. Current density J is not always uniform over S. By summing up every current density J passing through each infinitesimal surface that constutes the whole surface area, we get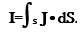

Resistance R

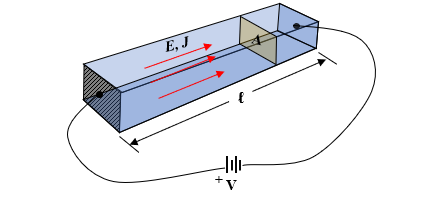
If a conductor of uniform cross-sectional area A and length ℓ has a voltage difference V between its ends, then:

at constant fields V = Vf - Vi = Ed ,where d represents the distance from the initial to final shift of voltage value. In this case d= ℓ.

assuming current is uniformly distributed over the area A.

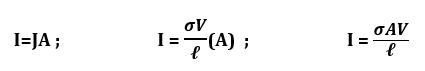
since Ohm’s Law states that V=IR;

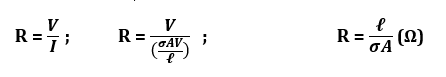
for non-uniform current distribution; the resistance equation becomes:

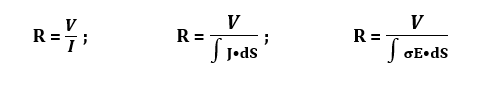
and if E is known rather than the voltage differences between the two faces, the resistance is given by

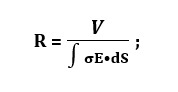
recall that the voltage potential is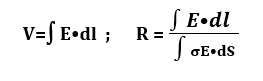

Reference: Edminister, Joseph A. Schaum's Outlines: Electromagnetics, 4th Edition,

All figures used in this article were created using Microsoft Word.