Sequences: Functions with fantastic properties – Some known sequences: Geometric Sequences
Hello dear friends Steemians! Continuing the series of posts on the fantastic sequences, in the present I will talk about the geometric sequences and some of its properties.
Definition of a Geometric Sequence – Recurrence Formula
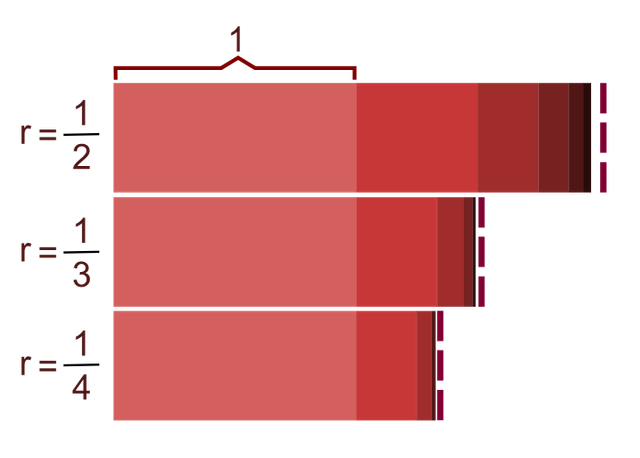
A geometric sequence or geometric progression is a sequence such that "the ratio or quotient between any two consecutive terms is constant" [1], that is, one in which any term is equal to the previous one multiplied by a constant called ratio for the progression or simply ratio.
For the geometric progression whose terms are:
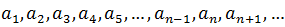
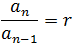
The previous expression, which is the recurrence formula of a geometric progression, shows that each term of the same is obtained from the previous one, multiplying it by the reason of the sequence. It is also common to rewrite it as:
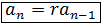
Some examples of geometric progressions are:
Example 1: The sequence of the powers of 2:
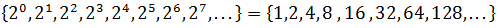
whose ratio is 2 (it is observed that when dividing two consecutive terms the result is always 2).
This sequence is of great importance in Mathematics and Computational Sciences, since it is related to the famous binary numbers (base numbering system 2).
Example 2: The sequence of the powers of 10:
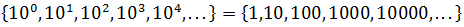
whose ratio is 10 (it is observed that when dividing two consecutive terms the result is always 10).
This sequence is of importance in Mathematics and Physics, since it is related to the very useful scientific notation and, of course, to the system of decimal or base 10 numeration.
General or n-th term of a Geometric Progression
From the recurrence formula of a geometric progression, the formula of the n-th or general term of a geometric progression is obtained:
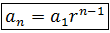
This formula allows obtaining any term of a geometric sequence known first and the ratio, without needing to know the preceding terms.
Sum of the first terms of a Geometric Progression
Following a procedure similar to the one used to obtain the formula of the sum of the first terms of an arithmetic sequence (read the previous post of the series, in the end I leave the link), we obtain the formula for the sum of the first n terms of a geometric progression:
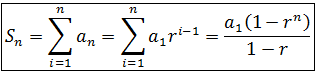
Note: The equations were written in the Word equation editor.
Sources cited:
[1] Geometric progression – Wikipedia.
Sources consulted:
[2] Fundación Polar, 2004. El Mundo de la Matemática. Fascículo 2. Sucesiones. Caracas: Últimas Noticias.
[3] Santillana, S.A. 2008. Matemática Primer Año (Programa de articulación). Cavelibro, Caracas.
[4] Navarro, Enrique. 1990. Matemática 1. Editorial Santillana, S.A. Caracas.
[5] Larson, Ron y Edwards, Bruce. 2010. Cálculo de una variable. Novena edición. McGraw-Hill/Interamericana Editores, S.A. México.
I hope the post was of your interest and pleasure. If you have any question or suggestion, I invite you to leave your comment and I will gladly answer. Thanks for your kind reading.
Next, in case it is of your interest, I leave the links to the previous posts of the series:
Sequences: Functions with fantastic properties – An Introduction.
Sequences: Functions with fantastic properties – Some known sequences: Arithmetic Progressions.
In the next installment, I will talk about another of the known sequences, the famous Fibonacci sequence.
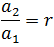
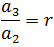
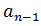
Nice
Thanks @desayner!
Iya
Excelente post, saludos.