PARTICLE PHYSICS: QUARKS BRING ORDER OUT OF CONFUSION.
The ways described in my last post titled "The Search for Order and the Classification of Particles", for classifying particles were immensely helpful – interactions could be
predicted. But like the Periodic Table in Mendeleev’s day, there was no underpinning
theory or model of particles which explained why the
patterns existed.
Then a revolutionary new theory was suggested to explain the ‘threeness’ referred to opposite: the heavy particles (baryons) might in fact be simple combinations of three smaller particles. This theory required a startling idea, that electric charge has to be subdivided into thirds: the new particles could have charges of 1/3 or 2/3 of the electronic charge.
At the time, very few physicists believed in the real existence of these hypothetical particles, at first not even the American physicist Murray Gell-Mann born 1929), who suggested the new particles and named them quarks.
Top antitop quark event. Raeky, public domain
This theory was later supported by experiments in which individual protons were bombarded by very energetic electrons. Just as the Geiger-Marsden alpha particle bombardment experiment showed that the atom has a small central mass, so these experiments showed that the density of a proton was not uniform, suggesting that it was made up of even smaller masses. These turned out to be the quarks.
The quark model of hadrons
The original simple quark model said that there were three quarks. These are now called the up, down and strange quarks. They are summarised in the table below. As well as having fractional charge, quarks also have fractional baryon number.
The first quarks
| Quark | Symbol | Charge/e | Baryon num. | Strangeness |
| Up | u | +2/3 | +1/3 | 0 |
| Down | d | -1/3 | +1/3 | 0 |
| Strange | s | -1/3 | +1/3 | -1 |
The table below shows how these basic
quarks are arranged in the most common baryons: protons and neutrons. The
combination of fractional charges on the quarks explains why protons are
positive and neutrons have no net charge.
Quarks in protons and neutrons
| Proton | u | u | d | Neutron | u | d | d | |
| Charge | +1 | +2/3 | +2/3 | -1/3 | 0 | +2/3 | -1/3 | -1/3 |
| Baryon no | +1 | +1/3 | +1/3 | +1/3 | +1 | +1/3 | +1/3 | +1/3 |
| Strangeness | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
ANTIQUARKS
But of course, quarks must have antiquarks, and these were needed to explain the existence of mesons (the middleweight hadrons). There are also three original antiquarks. In antiquarks, charge and strangeness have swapped over compared with the corresponding quarks. Antiquarks combine to produce the antiproton and the antineutron – and shows how a neutral particle can have an antiparticle version.
QUARKS IN BARYONS
Note that all baryons are made of quarks and all antibaryons are made of antiquarks. The baryon number of a quark is +1/3 and of the antiquark -1/3, which explains why the baryon numbers are either +1 or -1 for these particles.
QUARKS AND ANTIQUARKS MAKE MESONS
The significant difference between mesons and baryons (both are types of hadrons) is that mesons have baryon number 0. This is because mesons are made up of a quark and an antiquark, whose baryon contribution always cancels out. π- is the antiparticle of the π+: what was a quark in the particle has become an antiquark in the antiparticle, and vice versa. It also shows that some particles are their own antiparticles – changing an up quark for the up antiquark and vice versa makes no difference to the π°.
WHY SINGLE QUARKS DON’T EXIST
Quarks are ‘invisible’: they never appear on their own. Whenever there is enough energy to pull apart a pair of quarks in a pion, the energy is always enough to create two more quarks, which combine to form another pion. So all we see – and all we get – are pions.
AND ANOTHER THING… COLOUR
Some combinations of quarks might seem possible – but have never been found to exist. To explain this yet another property has been given to the hard-working quark: colour (or colour charge). The rule is that only colourless (or white) combinations can exist. Just as white light can be created by mixing red, green and blue (the primary colours) so baryons can be made with only a combination of three quarks that produce a colourless result. So a proton has a blue up, a red up and a green down quark. A quark can carry any colour, so that an up quark can be red, blue or green. The figure below shows quark colour combinations for the proton and the neutron.
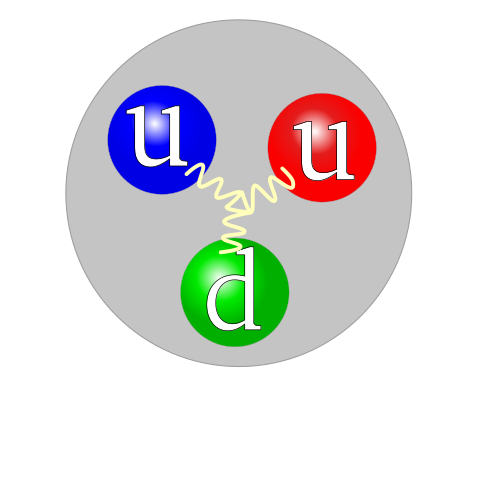
But how can a two-quark object like a meson manage to become colourless? Think about white light combinations: these can be made using secondary colours, e.g. yellow. Yellow is red plus green (or white minus blue). Yellow is often called ‘minus blue’. So antiquarks are needed – each carrying a ‘secondary’ colour, here called antiblue, antired or antigreen. Mesons are made from a quark and an antiquark, so that for example a π° meson can exist with a blue up quark and an antiblue up antiquark. Antibaryons contain only antiquarks with anticolours.
THE REALLY FUNDAMENTAL PATTERN (POSSIBLY)
After accepting the quark model in the late 1960s, physicists noticed a new kind of symmetry – this time between leptons and quarks. Leptons contain no quarks (they are indivisible), and everything else does, so it makes sense to think of leptons and quarks as the basic, really fundamental building block of matter. The table below shows the pattern of leptons and quarks known by 1974 (omitting antiparticles).
Lepton and quark families known about in 1974
| Leptons | Quarks | ||||
| Q = -1 | e- | μ- | u | ? | Q = +2/3 |
| Q = 0 | ve | vμ | d | s | Q = -1/3 |
The pattern suggested that a quark should
exist in the gap above the strange (s) quark. It was expected to have a charge
of +2/3, and theory predicted that hadrons containing this quark should have
masses of about 3 GeV/c2. Late in 1974, two laboratories announced
the discovery of two new heavy hadrons, the J and psi (Ψ) particles. They turned out to be the same particle, with a mass of
3.1 GeV/c2. Confusingly but appropriately, it is called the J/Ψ.
CHARM ENTERS PHYSICS
Physicists then realised that the new particle was a heavy meson containing the predicted missing quark, carrying yet another conserved quantity called charm. The J/Ψ consists of two charmed quarks, one the antiquark of the other (cċ). The new J/Ψ particle was predicted, but in the search for it, evidence was found for a particle that was not predicted at all. This was a new lepton – but an amazingly massive one, twice as heavy as a proton. This third kind of lepton was named the tau τ.
This discovery ruined the existing pattern between leptons and quarks and if the lepton-quark pattern was to be preserved it meant that yet another pair of quarks should exist. Quarks are never found alone, they have to be found indirectly – by finding particles with properties and interactions that could only exist if they carry the properties of their component quarks. Physicists named the new quarks top and bottom from their positions in the table and had to invent two new conserved quantities, topness and bottomness.
Top and bottom quarks were predicted to be much more massive than other quarks, and so should produce equally massive combinations. Such particles need a great deal of energy to be created, and the new proton synchrotron opened in 1975 at Columbia University (New York State) with an energy of 30 GeV very soon found a new massive particle that was a combination of a bottom quark and an antibottom quark. This b meson was named the upsilon, Y. It has a mass of 9.5 GeV/c2.
THE SEARCH FOR THE TOP QUARK
The missing piece of the jigsaw was the top quark. It was predicted to have a mass of more than 90 GeV/c2, twenty times as massive as a bottom quark. A particle containing a top quark would have a mass greater than this. The energy needed to produce such a massive particle is available when protons are made to collide with antiprotons in powerful synchrotrons. This was possible in the 1800 GeV Tevatron collider at Fermilab (Chicago, USA), and in April 1994 evidence for the existence of the top quark was announced. Experiments in March 1995 matched a mass of about 175 GeV/c2 for the top quark. In 2011, when the Tevatron collider at Fermilab has stopped functioning, the Large Hadron Collider at CERN, with a center-of-mass energy 7 TeV became the only accelerator that produces top quark.source
Units of mass and energy in particle physics
Obeying the laws of relativity, the mass of a particle varies with its speed. This means that we have to use the value of its mass when it is not moving, its rest mass. The principle of relativity also requires that mass and energy are equivalent, linked by the Einstein formula E = mc2. In fact, particle physicists measure mass in energy units.
Investigations usually involve charged particles which are accelerated by high voltages and gain mass-energy as they accelerate. It is convenient for particle physicists to measure energy and therefore mass in terms of an electrical unit, namely the electronvolt, eV.
One electronvolt, 1 eV, is the energy gained by a particle carrying the electronic charge e = 1.6 × 10-19 C when it moves through a potential difference of 1 V.
1 eV = 1.6 × 10-19 C × 1 JC-1
= 1.6 × 10-19 J
And 1 J = 6.25 × 1018 eV
The mass of a proton is 1.6726 × 10-27 kg. In energy units, this is equivalent to:
Ep = mpc2 = 1.6726 × 10-27 × (3 × 108)2 J
= 1.5053 × 10-10 J
REST MASS IN GeV/c2
The mass-energy of a proton is about 109 eV, or 1 GeV, a nice easy number to work with. We need to be careful with this unfamiliar set of units. For example, from the Einstein formula we have:
m = E/c2
so we can put
m = Energy in eV / (light speed)2
= GeV / c2
Thus the rest mass of a proton mp is written as 1, with units GeV/c2, or:
mp = 1 GeV/c2 =1 GeV c-2
THE AMAZING IMPLICATIONS OF UNCERTAINTY PRINCIPLE
The uncertainty principle (explained vividly below) has some amazing consequences for particle physics. It implies that a quantum of energy can exist for a very short time, provided that the product of energy and time is less than the value of the Planck constant, that is, if ΔEΔT < h/4π.
This also applies to matter, since energy and matter are equivalent. So particles could also exist for very small times. These particles, called virtual particles, can be produced without breaking the law of conservation of mass-energy. The significance of this feature of the uncertainty principle is seen as fundamental to a description of the nature of matter, as it exists now and in the early stages of the Universe.
THE UNCERTAINTY PRINCIPLE
At the heart of particle physics is the idea of an uncertainty throughout nature, though not the everyday physical uncertainty caused by imprecise measurements or the use of techniques that cannot measure every factor in a complex situation.
In 1927, the German physicist Werner Heisenberg (1901-1976) showed that there was an inbuilt uncertainty in the ability to measure the state of any small particle, such as an electron or a photon, however accurate the instrumentation. His uncertainty principle has since been developed beyond the simple problem of measurement into a statement about the fundamental nature of the Universe.
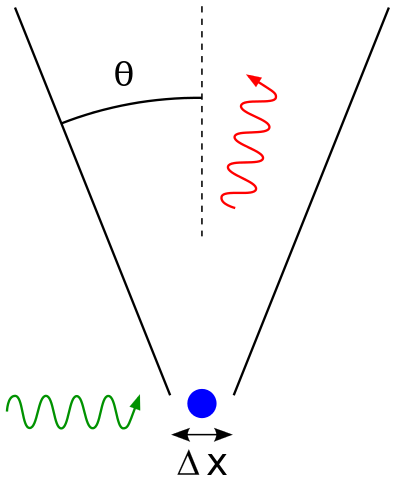
Heisenberg imagined an experiment to measure the momentum and position of, say, an electron. One way of doing this would be to use an ‘imaginary microscope’ that could see the electron. This could only happen if a photon hit the electron and bounced back into the eyepiece. But the photon carries momentum and by its interaction with the electron would exchange some (unknown) fraction of its momentum, so that the electron would no longer have its original momentum.
You could try to make this uncertainty in the momentum very small by using a photon of very small momentum. But a photon is also a wave that extends over space, having a characteristic wavelength λ. The position of the electron would not be determined to an accuracy better than the value of λ, and the smaller its momentum the larger is the wavelength of the photon. This means that by using a low momentum (low-energy) photon we improve our knowledge of the electron’s momentum, but lose accuracy in determining its position.
The incoming photon has momentum h/λ, where λ is its wavelength and h is the Planck constant, value 6.6 × 10-34 Js. The photon could transfer all this momentum to the electron. Thus the collision has produced an uncertainty in the electron’s momentum of:
Δp = h/λ
As explained above, the uncertainty Δx in the position of the electron is of the order of the light wavelength, so we can put Δx = λ. Multiplying both these uncertainties gives:
ΔpΔx = (h/λ) λ = h
This represents the best possible accuracy. In practice, we must accept that the uncertainty is always greater, so we write:
ΔpΔx ≥ h [1]
The momentum-position formula.
This is Heisenberg’s simple treatment of the uncertainty principle. A fuller derivation gives:
ΔpΔx ≥ h/4π
The uncertainty is not due to any method of measurement, but is in the nature of the moving object, whether a photon, an electron, a spaceship or anything else.
Uncertainty in energy and time
There is also an uncertainty in the energy of a photon or an electron; both have a wave and a particle aspect. The energy E of a photon of frequency f, for example, is given by E = hf.
Now think about trying to measure this energy by measuring the frequency. Suppose our frequency measurer is able to identify one wave (as above) and so measure to an accuracy of 1 Hz, and we try to measure the frequency of a 1 000 Hz wave.
In 1 second we can say, f = (1000 ± 1) Hz. The uncertainty in the result is Δf = 1. We can do better by taking a reading for a longer time, say 20 s, so that we measure 20 000 wavelengths.
Then the result could be put as (20 000 ± 1)/20. This gives an uncertainty Δf = 1/20.
So for Δt = 1, Δf = 1. For Δt = 20, Δf = 1/20.
In both cases: ΔfΔt = 1 [2]
This is true, however accurate the measurement. Now, both photons and particles are wavelike, with energy and frequency linked by E = hf. So we can write:
Δf = ΔE/h
and from equation 2:
ΔfΔt = ΔEΔt/h = 1
giving: ΔEΔt = h
Again, this is the best possible result, so in general we have an uncertainty principle involving energy and time that says:
ΔEΔt ≥ h [3]
The energy-time formula
Again, a more accurate relationship is
ΔEΔt ≥ h/4 π
This means that if we wish to measure energy accurately we must take a long time to do the measuring.
Till next time, I remain @emperorhassy.
Thanks for reading.
REFERENCES
https://www.learner.org/courses/physics/unit/text.html?unit=1&secNum=5
https://phy.duke.edu/~kolena/modern/hansen.html
https://www.livescience.com/64687-why-top-quark-so-heavy.html
https://www.britannica.com/biography/Murray-Gell-Mann
https://en.wikipedia.org/wiki/Murray_Gell-Mann
http://www.nucl.phys.tohoku.ac.jp/sansha/2011/lecture_files/PART-II.quark_model.pdf
https://en.wikipedia.org/wiki/Quark_model
https://en.wikipedia.org/wiki/Quark
https://www.britannica.com/science/antiquark
https://en.wikipedia.org/wiki/Baryon
https://en.wikipedia.org/wiki/List_of_baryons
https://en.wikipedia.org/wiki/List_of_mesons
https://en.wikipedia.org/wiki/Meson
https://www.britannica.com/science/subatomic-particle/Quarks-and-antiquarks
https://medium.com/starts-with-a-bang/there-are-no-free-quarks-ddec8cb831ea

Your post has been manually curated by FreeVoter Team.You can earn liquid steem by delegating SP to @freevoter !! We are now paying 100% daily earnings and 90% curation reward to our delegators !! Join Discord for more information. Thank you !!
Hello,
Your post has been manually curated by a @stem.curate curator, @riccc96.
We are dedicated to supporting great content, like yours on the STEMGeeks tribe.
If you like what we are doing, please show your support as well by following our Steem Auto curation trail.
Please join us on discord.
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having used the steemstem.io app and included @steemstem in the list of beneficiaries of this post. This granted you a stronger support from SteemSTEM.