PRINCIPLES AND APPLICATIONS OF X-RAY DIFFRACTION METHODS: SOLID SUBSTITUTIONAL SOLUTIONS (I)

A warm greeting from members of the Steemit community. I am a chemist, and for ten years I have been working in the area of crystallography; Preparing, assembling, measuring and analyzing polycrystalline samples by X-ray diffraction. In the course of my professional life I have analyzed samples of semiconductors, minerals, clays, catalysts, activated carbons, nanocomposites, among others.

From a series of post, I would like to share my experience in the area of X-ray diffraction with you. I want to tell you about the principles and applications of X-ray diffraction methods: the generation of X-rays, the instrumental part of a diffractometer, the sample carriers used, the types of assembly, the data collection and treatment, qualitative analysis and quantitative, determination of cell parameters, specialized programs used, among other aspects.

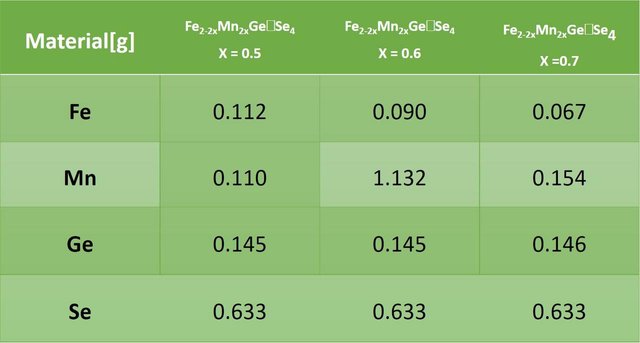
My first experience with the technique was from the synthesis and characterization by X-ray diffraction of a solid substitutional solution of the solid material Fe2-2xMn2xGe Se4 with compositions X = 0.5, 0.6 and 0.7 (where the Fe gradually is replaced by the Mn , passing from a structure Fe2GeSe4 to MnGeSe4, when X = 0 or X = 1, respectively) belonging to the family of semiconductor compounds of type II2IVVI4.

This work is basically composed of two parts: 1. The synthesis of the semiconductor material (Fe2-2xMn2xGe Se4 with compositions X = 0.5, 0.6 and 0.7), taking into account the theory of solid substitutional solutions, and 2. The characterization by XRD ( qualitative analysis, refinement of cell parameters and determination of the spatial group) of the three compositions. In this sense, in this post I want to talk about the first part and in a second post I will talk about the second part.

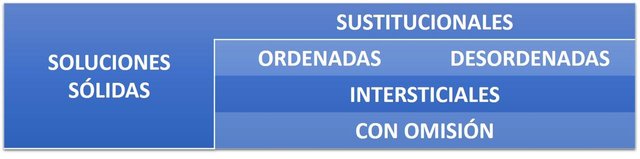
SOLID SOLUTIONS

In a perfect crystal all the atoms of the structure should be in their correct positions of the network. This situation can only exist at the temperature of absolute zero, 0 degrees Kelvin. Above 0 degrees Kelvin appear the defects in the structure. These defects can be of two main types: intrinsic defects, inherent to the crystal (the total composition does not change and therefore are also known as stoichiometric defects); and extrinsic defects, which are created when a foreign atom is inserted into the network, the solid thus formed is a non-stoichiometric compound because the ratio of the atomic components is no longer a simple whole number, (Smart, 1995).

Most minerals are not pure substances, but have a variable chemical composition. This is due to the frequent substitutions of certain ions or ionic groups that have similar ionic radius (differences <15%) and electric charge (for example, Mg + 2 for Fe + 2, in octahedral positions or Al + 3 for Si + 4 in tetrahedral positions, etc.). In the last examples, in order to maintain the electrical neutrality of the structure, other additional substitutions must take place. As a result of these substitutions, solid solutions are produced in which, in a structure, two or more different elements appear with the possibility of occupying the same atomic position in different proportions. Although the term solution is commonly associated with liquids and is defined as a homogeneous mixture (which presents a single phase) between the majority component (solvent) and another that is in smaller proportion (solute), with the solids a similar situation can occur. By solid solution we mean that the constituents are atomically dispersed, some of the places are occupied by one class of atoms and the others by atoms of the other class. It is not a compound in the strict sense, since solid solutions can generally exist with a widely variable composition, while chemical compounds have constant composition (Christy, 1971). There are limits of solubility in solid solutions but there are important exceptions to this rule, for example: solid solutions of copper and nickel and those of silver and gold. Copper dissolves any amount of nickel that is added to it and vice versa. The same goes for solid silver and gold solutions. Examples in which there is a limit occur in solid solutions of copper in silver or silver in copper, copper dissolves a maximum of 8% of silver, and the latter metal dissolves a maximum of 8.8% of copper. In general, the more different the components are, both from the chemical point of view and as regards the atomic or molecular size, the more restricted the partial solubility will be (Keyser, 1972).

There are different types of solid solutions:

SOLID SUBSTITUTIONAL SOLUTIONS.

Law of Vegard (Polonio, 1981). A substitution of one element for another occurs in the entire range of possible compositions determined by the compositions of two end members. A good example of this type of solutions is the one that forms the isomorphic series of olivine, (Mg, Fe) 2SiO4. (uned.es). In olivine, Mg + 2. can be partially or totally replaced by Fe + 2, constituting a complete solid solution between the two extreme terms forsterite (Mg2SiO4) - fayalite (Fe2SiO4). Another example is that formed by the carbonates of the rhodochrosite series MnCO3 - siderite FeCO3. But there are also anionic substitutions, such as the one formed by the complete solid solution KCl-KBr, in which the Cl- and Br- anions substitute each other.

The substitutional solid solution originates whenever the atoms of a metal A are lodged in the crystalline network of another metal B, replacing it in the positions or crystallographic coordinates that it occupies in it. Generally, this substitution is done in a fortuitous or disorganized manner, that is, without the solute A, being placed in systematically privileged positions of the crystalline network of solvent B. This type of solid solution is produced between the elements with similar atomic volumes. The miscibility or exchange capacity of one atom for another as a function of temperature can be 100%, in which case the solid solution is Isomorphic or continues. In an isomorphic system only a single type of crystalline structure is found, whatever the proportions of the components. In this case, the crystalline structures of metals A and B must necessarily be equal and their relative atomic diameters (size factor) can not differ by more than approximately 15%, and certain conditions must also be fulfilled in the valence states of the metals In the range of concentrations where the solid solution is continuous, there are no changes of intermediate phases or structures; the only modification that the basic crystalline network undergoes is a slight variation in the value of its crystallographic parameters, depending on the differences between the atomic radii and the relative concentrations of the solvent and the solute. If the radius of B is greater than that of A, the volume of the cell of the latter increases with the concentration of that and vice versa, provided that there are no particular circumstances that modify the characteristics of interatomic bonds. The corresponding variation of the values of the parameters of the cell as a function of the percentage atomic composition, is almost linear in binary systems of a single phase of homogeneous substitutional type, especially in ionic or metallic networks of cubic type, as manifest Vegard's law. But in general, all systems show more or less known deviations from the theoretical behavior; in most cases these deviations tend towards the direction of network concentration.

Vegard's Law provides a fairly direct method to theoretically determine the composition of a solid solution is continuous or not; for this, it is enough to measure precisely one parameter of the unit cell and refer to a calibration curve in which the abscissa is the percentage of the substituted atom and the ordinate is the value in Anstromgs of the parameter a of the unit cell, (Polonio, 1981 ).

SYNTHESIS OF SOLID SUBSTITUTIONAL SOLUTIONS

For the synthesis of the different compositions (X = 0.5, 0.6 and 0.7), pure elements of Magnesium (Mn), Iron (Fe), Germanium (Ge) and Selenium (Se) were used. The amount needed to complete a gram for each of the different compositions was weighed. The following describes the elements used and the quantities used for each of the syntheses.

To make the synthesis of the different compositions (X = 0.5, 0.6 and 0.7) of the Fe2-2xMn2xGeSe4 material, a one zone oven was used. The furnace was prepared by the personnel of the Condensed Matter Research Laboratory of the School of Physics of the UIS.

REFERENCES

SMART, L y MOORE, E. Química del estado sólido : Una introducción. Wilmintong, Delaware, E.U.A : Adison-Wesley Iberoamericana, 1995. P. 101-169.

CHRISTY, Robert W. Estructura de la materia : Una introducción a la física moderna. Barcelona : Reverte, 1971. p 238.
KEYSER, Carl A. Ciencia de materiales para Ingeniería. Mexico : Limusa-Willey, 1972. p 140.

POLONIO Bermudez. Joaquín. Métodos de difracción de rayos X : Principios y aplicaciones. Madrid : Pirámide, 1981. 461p.

Thank you very much my community for the attention you can give to this publication, I hope your questions or suggestions.

Until a next opportunity