Einführung in die komplexen Zahlen
Grundlagen der Zahlenarten
Grob Zusammengefasst:
Zuerst kommen die Natürlichen Zahlen zu denen, je nach Definitionsart, auch die Null dazu gehört. Zu ihnen gehören die Zahlen 1,2,3,4 usw, mit denen man Dinge wie Geld, Nahrungsmittel oder Personen zählen kann. Später kam der Bereich der Ganzen Zahlen hinzu, womit nun auch negative Zahlen, z.B. bei Bankkonten deshalb auch Schulden, abgebildet werden konnten. Zu den Natürlichen Zahlen hinzu kamen jetzt die -1 -2 -3 usw. Um die Zwischenschritte ausfüllen zu können, benötigte es nun die Gebrochenen Zahlen wie z.B. 1/2, 1/5 usw., an die sich die rationalen Zahlen anschließen, die auch Brüche wie (1/7) oder -(1/60) erlauben. Irrationale Zahlen hingegen, sind die Zahlen, die sich eben nicht als Bruch darstellen lassen wie z.B. die Kreiszahl pi. Darauf folgen die reellen Zahlen, die als Zusammenfassung rationaler und irrationaler Zahlen gelten.
Man erkennt, dass jede hinzugefügte Zahlenart als Teilmenge die vorherigen Arten beinhaltet
Nach den reellen Zahlen kam aber noch ein weiterer Bereich dazu:
Die komplexen Zahlen
Eine Gleichung der Art
x²+1=0
x²=-1 x= √ -1 -> !
hat bekanntlich keine Lösung, da die Wurzel aus -1 nicht gezogen werden kann. Um eine solche Berechnung zu ermöglichen, führte Leonhard Euler (1707-1783) die Anwendung des Buchstaben i ein. Dieser erweiterte den bisherigen Zahlenbereich der reellen Zahlen durch Einführung der imaginären Zahl i mit der Eigenschaft:
i²= -1.
Sie ergibt, mit sich selbst multipliziert, folglich eine negative Lösung:
i*i = -1
und kann deshalb keine reelle Zahl sein, da diese mit sich selbst quadriert keine negative Lösung ergeben können:
-1*-1= 1
1*1= 1
Die komplexen Zahlen setzten sich aus zwei Teilen zusammen: Dem Realteil (a) und dem Imaginärteil (b*i)
In Worten steht hier:
Zahl = Realteil + Imaginärteil * i
Hierbei sind a und b jeweils reelle Zahlen wie man sie kennt und i die imaginäre Einheit, die oben eingeführt wurde. Zur Bezeichnung verwendet man meistens das obige z, wobei in der Elektrotechnik ebenfalls der Buchstabe j üblich ist, da i für die Stromstärke vorbehalten ist.
Anwendung
Benutzt werden sie unter anderem zur vereinfachten Berechnung von Schwingungsvorgängen und Wellen. Auch in der Fouriertransformation oder der Mandelbrotmenge finden sie Anwendung. Außerdem werden sie zur Lösung von Differentialgleichungen sowie Signalverarbeitungen und ebenfalls in der Quantenphysik zu verschiedensten Rechnungen verwendet.
Beispiel:
2-6i
Hier ist der Realteil nun 2 und der Imaginärteil -6 (das i wird nicht dazu gezählt).
Für die komplexen Zahlen gilt, ebenso wie für alle anderen Zahlenbereiche auch, das Permanenzprinzip. Somit enthält der neue Zahlenbereich die zuvor genannten, ebenfalls als Teilmenge. Eine reelle Zahl ist deshalb nur eine komplexe Zahl, deren Imaginärteil 0 entspricht. Natürlich gibt es auch rein imaginäre Zahlen. Bei diesen entspricht umgekehrt der Realteil 0. Das Permanenzprinzip legt außerdem den Erhalt der Rechenregeln fest. Für komplexe Zahlen gelten das Assoziativgesetz, das Kommutativgesetz und das Distributivgesetz. Eine Besonderheit ist, dass sie keine Ordnungsstrukturen besitzen, durch die man Vergleichsaussagen über die Größe zweier Zahlen treffen kann. Ein Vergleich wie 2>1, funktioniert in diesem Zahlenraum nicht mehr.
Rechenbeispiele:
Addition und Subtraktion:
Bei dieser Rechenoperation addiert/subtrahiert man jeweils die Real- und die Imaginärteile voneinander. Sind z= a+ bi und w= c+ di gegeben:
Beispiel:
Multiplikation
Es wird ganz normal ausgeklammert:
Beispiel:
da i²=-1, wird aus 12i² -> -12 und somit 6-12=-6
Division
Konjugation
Bevor man komplexe Zahlen dividiert, schaut man sich die Konjugation an. Durch diese erhält man den reziproken Wert, d.h. den Kehrwert der Zahl z der durch 1/z festgelegt ist, da (1/z) * z = 1 ist. Graphisch entspricht die Konjugation einer Spiegelung an der reellen Achse und wird durch Vertauschung des Vorzeichens von dem jeweiligen Imaginärteil realisiert. ~Der Trick besteht bei der Division darin, mit dem konjugierten Nenner zu Erweitern:
Beispiel
Die Rechnung im Nenner wurde mit orange und die im Zähler mit blau gefärbt. Der zweite Bruch mit dem multipliziert wurde, ist die zuvor angesprochene Erweiterung mit dem komplex konjugierten Nenner, durch welchen selbiger letztendlich reell wird, da +di² und -di² sich auslöschen. Im Beispiel geschieht die Auslöschung durch -8i+8i=0.
Die Gauß'sche Zahlenebene
Diese Zahlen graphisch darzustellen, gelang Karl Friedrich Gauß ( 1777-1855 ) durch folgende Methode:Eine komplexe Zahl z=a+b*i kann man in einer Gauß'schen Zahlenebene durch ein Koordinatenpaar (x/y) darstellen. Hierbei liegen die reellen Zahlen auf der x-Achse, was vergleichbar mit einem Zahlenstrahl ist. Auf dem Zahlenstrahl liegen alle Zahlen von + bis - unendlich:
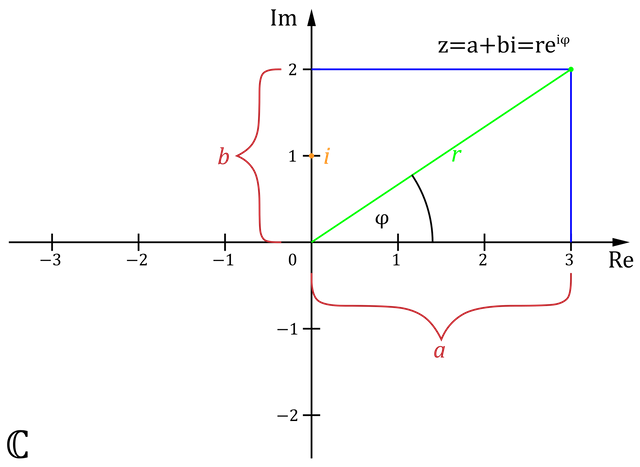
Jedoch kann eine imaginäre Zahl nicht auf der selben Achse untergebracht werden, weshalb eine weitere Achse hinzugefügt wird. Man erhält eine x- und eine y-Achse und kann die komplexen Zahlen in diesem kartesischen Koordinatensystem wie Vektoren einzeichnen und mit ihnen rechnen:
Das C unten links ist das zugehörige Zeichen für die komplexen Zahlen
Da die komplexe Zahl der Form z= a+b*i aus zwei Teilen besteht, geht man nun erst auf der x-Achse die benötigten Schritte für a und danach auf der y-Achse für den imaginär Teil ib. Der Zahlenstrahl wurde also um eine Achse erweitert, die nun die Darstellung komplexer Zahlen in einem Vektorraum ermöglicht. Nimmt man die Zahl 2+1i, geht man 2 Schritte auf der x-Achse und von diesem Punkt aus und dann einen auf der y-Achse. Verbindet man diesen Schlusspunkt mit dem Koordinatenursprung, entsteht ein Dreieck. Über dieses lässt sich ,unter Anwendung des Phytagoras, den Betrag der komplexen Zahl ausrechnen. Zwei Seiten sind bekannt und die dritte als Strecke des Punktes zum Ursprung entspricht:
Außerdem kann dieser Betrag durch die Verwendung der Konjugation berechnet werden, indem man die Zahl z mit der konjugierten Zahl z multipliziert. Das Ergebnis ist ebenfalls:
Polarform
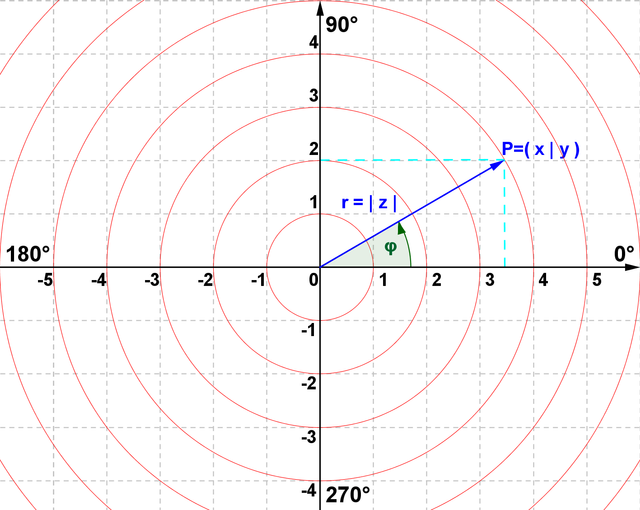
Neben der graphischen Darstellung in einer Gauß'schen Zahlenebene, gibt es zusätzlich noch die sogenannte Polarform. Hierbei handelt es sich nicht um Vektoren, sonder um Zeiger, die durch ihre Länge und den Winkel zur reellen Achse eindeutig festgelegt sind.
Wie auch schon zu Anfang, entsteht wieder ein Dreieck sobald man eine komplexe Zahl einfügt. Die Strecke von 0 zu P ist ebenfalls der Betrag unserer komplexen Zahl z. Über sinus und cosinus, kann man die Strecke auf der reellen und auf der imaginären Achse berechnen. Strecke a= |z| * cos alpha. cos = Ankathete/Hypothenuse.
Will man die Ankathete a berechnen, deren Strecke unserem Realteil entspricht, multipliziert man den cosinus mit der Hypothenuse:
cos alpha*Hypothenuse= Ankathete
Da die Hypothenuse der Betrag von z ist, schreibt man:
Für die Strecke b wird das Selbe berechnet, nur das in dem Fall der Sinus benutzt werden muss:
sin=Gegenkathete/Hypothenuse
Setzt man die obigen Ergebnisse in die allgemeine Gleichung z =a+bi ein, erhält man:
Ausgeklammert:
Eine weitere Formel hierfür ist die Euler'sche Formel bzw Euler'sche Identität:
Wobei:
Sie ist gleichzusetzen mit der obigen trigonometrischen Darstellung (siehe "Ausgeklammert:"). Diese Exponentialdarstellung ermöglicht oftmals eine vereinfachte Berechnung innerhalb vieler Anwendungsgebiete.
Zu diesem Themengebiet folgen demnächst noch genauere Fälle
Bis dahin und
Danke für's Lesen :)
Texthttp://www.math-kit.de/2002/demo2/CN-PB-XML-cob/rep//Manifest7/euler.htmlhttps://www.ethz.ch/content/dam/ethz/special-interest/dual/educeth-dam/documents/Unterrichtsmaterialien/mathematik/Komplexe%20Zahlen%20(Leitprogramm)/Leitprogramm.pdf https://www.massmatics.de/merkzettel/index.php#!1211:Division_komplexer_Zahlenhttp://www.uni-magdeburg.de/exph/mathe_gl/kzahlen.pdfhttps://medium.com/i-math/complex-numbers-explained-fad9a6793019https://de.wikibooks.org/wiki/MathGymOS/_Analysis/_Komplexe_Zahlen/_Die_Polarformhttps://www.tf.uni-kiel.de/matwis/amat/mw1_ge/kap_2/basics/b2_1_5.htmlhttp://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/3.2_Polarformhttps://de.wikipedia.org/wiki/Komplexe_Zahlhttp://www.mathepedia.de/Zahlenbereiche.htmlhttp://www.math-kit.de/2002/demo2/CN-PB-XML-cob/all/Manifest68/history.htmlhttps://www.mathebibel.de/komplexe-zahlenBilder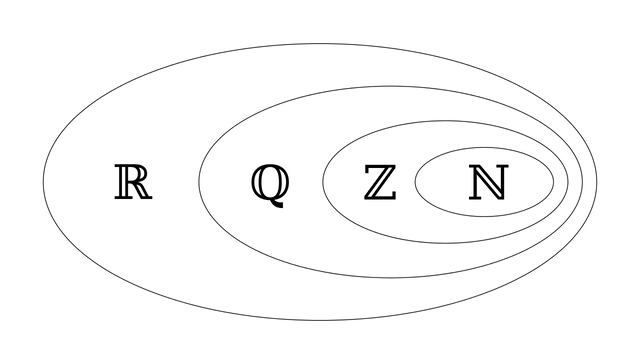
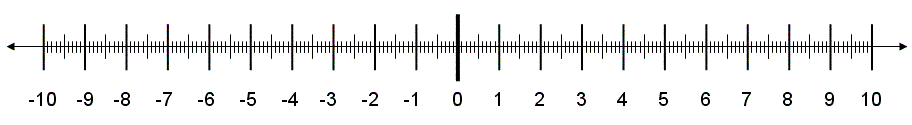
Alle Formeln wurden mit Word erstellt und auf meinem imgur Account veröffentlicht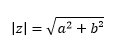
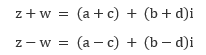
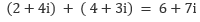
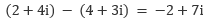
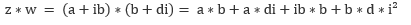
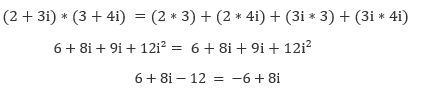
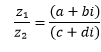
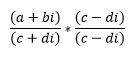
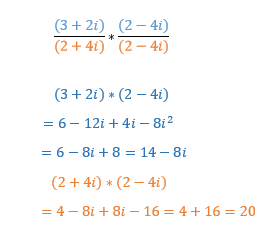
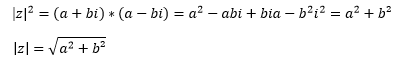
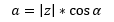
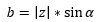
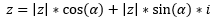
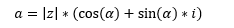
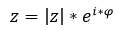
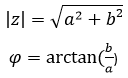
Ein Kurator von German-Steem-Bootcamp fand deinen Beitrag wirklich lesenswert und hat ihn deshalb Upgevotet, wenn du mehr über das GSB erfahren magst kannst du dich gerne bei uns im Discord melden : https://discord.gg/HVh2X9B
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
super geschrieben. In der Schule wurde mir Angst vor Mathe ankonditioniert. So geschrieben find ichs eingänglich und verständlich
Danke für das Lob :) Hatte selbst oft genug Probleme in Mathe, weil einfach nicht klar rübergebracht wurde, was genau man gerade überhaupt macht und warum man es so machen muss. Wenigstens versuche ich es jetzt weitestgehend zu verstehen :D