Geometría Descriptiva mediante SketchUp Parte IV: planos
Saludos y bienvenidos estimados lectores de este blog. Ya abordado el tema de las rectas, entraremos en el estudio de un lugar geométrico indispensable para lograr la representación de objetos en el espacio: el plano. En la Doble Proyección Ortogonal (DPO), la representación de un objeto tridimensional puede requerir conformar superficies planas para determinar la forma de estos y sus proyecciones en horizontal y en vertical. El programa SketchUp nos permite generar vistas tridimensionales de la situación y construir objetos en el espacio de una manera muy sencilla, constituyendo así un recurso computacional de gran ayuda. Durante mis estudios de Ingeniería Civil, utilicé este software en diversas ocasiones, no solo para entender mejor los temas de Geometría Descriptiva, sino para cualquier problema que requiera la representación tridimensional de un objeto.
Definición
Un plano en el espacio puede ser definido de diferentes maneras, cada una de estas busca un objetivo único: conformar un lugar geométrico de puntos que son coplanares entre sí. Para que esto sea posible, deben de darse ciertas condiciones mínimas. Al momento de construir una figura tridimensional en la DPO, cada una de estas maneras de generar un plano puede ser utilizada a conveniencia, de acuerdo a lo que se requiera para llegar a la solución deseada.
Las condiciones geométricas mínimas para definir un plano son tres. Las más usuales y prácticas son las siguientes:
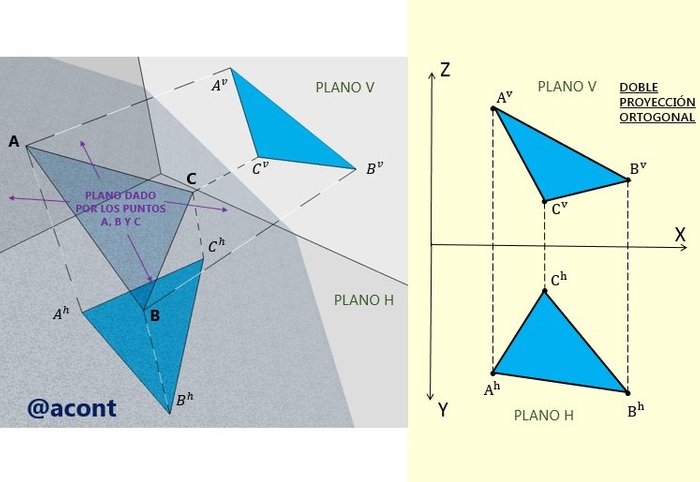
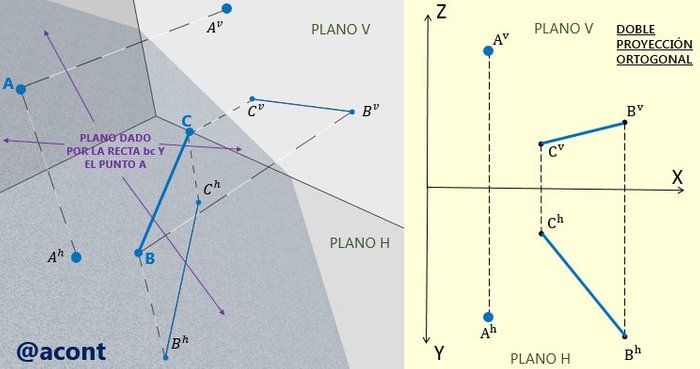
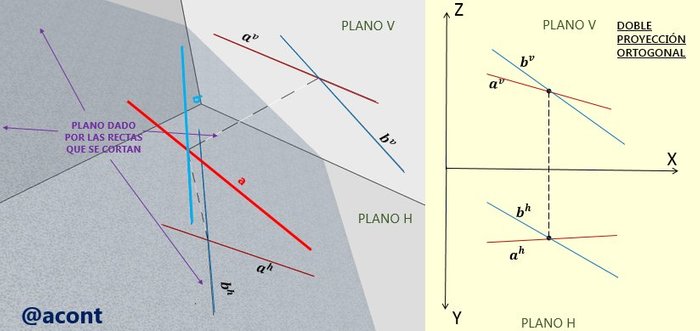
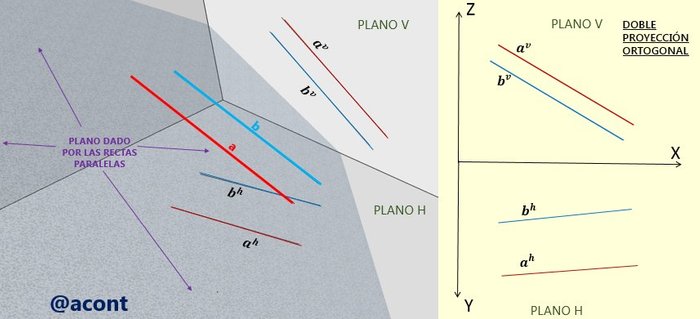
Cada una de estas cuatro maneras está relacionada de manera directa con las otras. Ya definido un plano, sea por tres puntos o dos rectas que se cortan, el mismo contiene infinitos puntos e infinitas rectas coplanares entre sí.
La nomenclatura utilizada para darle nombres a los planos suele ser dada por algún símbolo griego (por ejemplo “α”, “β” o “π”) o dos letras minúsculas que representan dos rectas contenidas en el plano (por ejemplo, dos rectas que se cortan “a” y “b” generan el plano “ab”).
Rectas y puntos dentro del plano
Supongamos que conocemos un plano dado por tres puntos “A”, “B” y “C”, una recta “a” y un punto adicional “D”. Esta situación se observa en la Fig. N°5, en la que se ha representado en el espacio y en doble proyección ortogonal el plano, la recta y el punto. La pregunta sería: ¿Cómo confirmamos que la recta “a” y el punto “D” se encuentran dentro del plano?
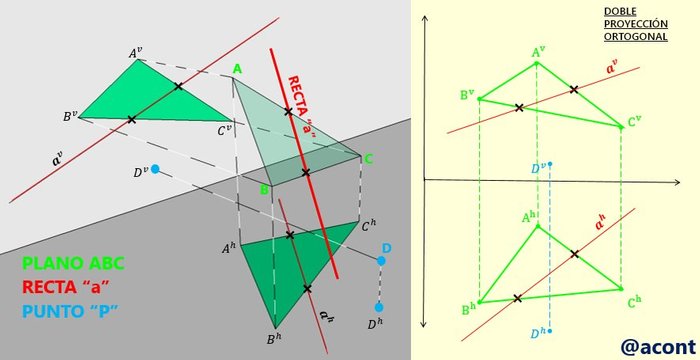
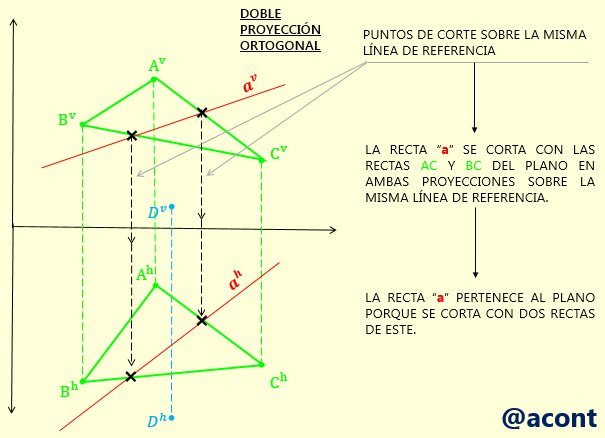
De las condiciones anteriores, sabemos que, si dos rectas se encuentran sobre el mismo plano, ambas deben de cortarse en algún punto para que sean coplanares. Entonces, para confirmar si la recta “a” se encuentra dentro del plano dado, esta debe de cortarse con mínimo dos rectas de este. De esta manera, en la DPO observamos que el punto de corte de la recta “a” con las rectas del plano se encuentra sobre la misma línea de referencia vertical, por lo que la recta “a” efectivamente se corta con dos rectas de dicho plano (Fig. N°6). Recordemos de la Parte III de esta serie de publicaciones que, si dos rectas no se cortan, el punto de corte en ambas proyecciones de la DPO no se encuentra sobre la misma línea de referencia vertical.
En el caso del punto “D”, la única forma de verificar que su ubicación está dentro del plano dado, es trazar por “D” una recta arbitraria que se encuentre dentro del mismo, es decir, nosotros la vamos a hacer pertenecer al plano. Para lograr esto, la recta debe cortarse con mínimo dos rectas de dicho plano, similar al caso anterior. En este caso, trazaremos una recta arbitraria “r” por “D” en su proyección horizontal que se corte con dos de las rectas del plano para así encontrar la proyección vertical de la recta arbitraria “r”. Si la proyección vertical de dicha recta arbitraria pasa por la proyección vertical del punto “D”, este punto estará dentro del plano (Fig. N°7). También se pudo haber trazado la recta arbitraria empezando por la proyección vertical.
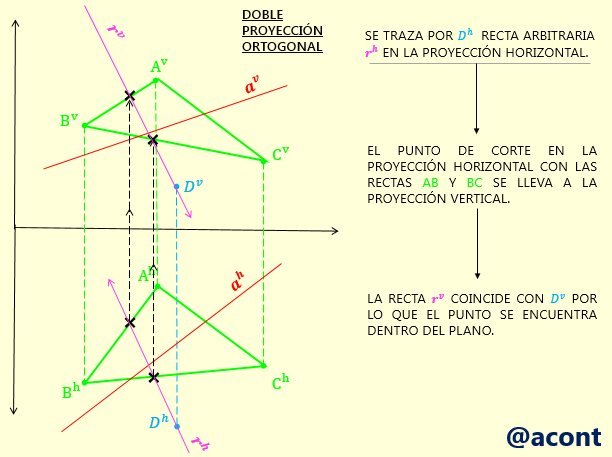
Cabe aclarar que el punto “D” no se encuentra dentro del triángulo dado por los puntos “A”, “B” y “C”, pero el plano formado por estos tres puntos se extiende hasta el infinito en todas las direcciones. El punto “D” pertenece al plano formado por estos tres puntos.
Posición relativa de un punto al plano
Esta vez, conocemos un punto “E” que no está dentro del plano (Fig. N°8). La pregunta que podemos hacernos es ¿Este punto está arriba o abajo, delante o detrás del plano?
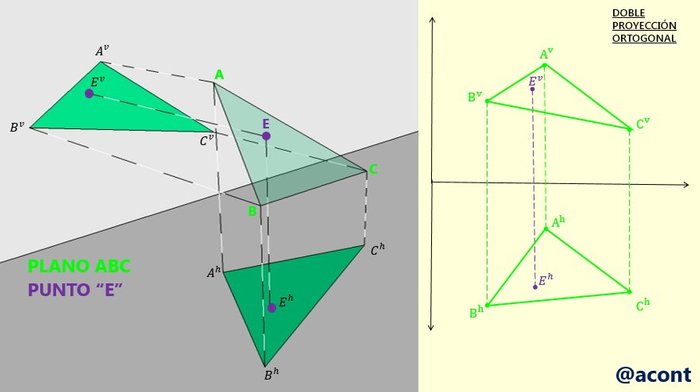
En la Figura N°8, se observa que en la DPO las proyecciones del punto “E” se encuentran dentro del área del triángulo tanto en el plano vertical como en el plano horizontal de proyección, sin embargo, esto no quiere decir que en el espacio el punto esté dentro del plano. No obstante, el punto “E” parece estar muy cercano al mismo.
La solución a esto es similar al caso anterior. Trazaremos una recta arbitraria que pase a través de una de las proyecciones del punto “E”, y luego, en la otra proyección, podremos observar la posición relativa de esta recta con el punto, ya que no van a coincidir.
Para este ejemplo, trazaremos una recta arbitraria a través de la proyección vertical del punto “E”. Al encontrar la proyección horizontal de dicha recta, haciendo que la misma se corte con dos rectas del plano, encontramos que la proyección horizontal del punto “E” se encuentra “delante” de dicha recta, ya que recordemos que la proyección horizontal de la DPO es el resultado de mirar los objetos en el espacio “desde arriba”. Esto se ilustra en la Fig. N°9.
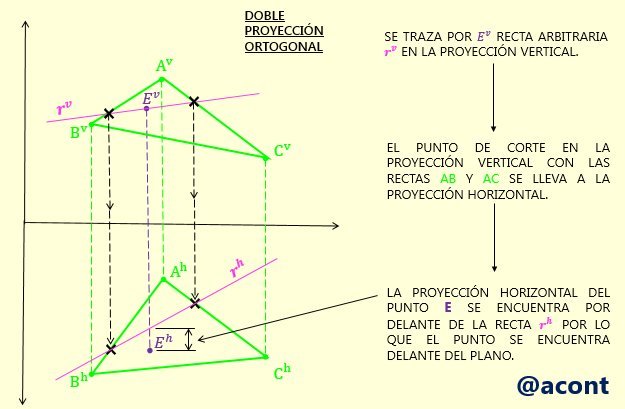
Si en vez de trazar una recta arbitraria por la proyección vertical del punto “E” se hubiera trazado en la proyección horizontal de este punto, encontraríamos que, en la proyección vertical, dicha recta se encuentra “por encima” de la proyección vertical de “E”, es decir, por encima del plano, tal como se observa en la Fig. N°8. En resumen, el punto “E” se encuentra detrás y por encima del plano dado.
Aportes de esta publicación
Se brinda a través del programa SketchUp vistas en el espacio de los planos y sus propiedades básicas para así incentivar el desenvolvimiento en las habilidades de representación de los mismos en la doble proyección ortogonal y la comprensión de los procedimientos necesarios para resolver problemas relacionados a estos.
Referencias Bibliográficas
•Osers et al (2012). Estudio de Geometría Descriptiva (14va Edición). Editorial Torino. Caracas.Fuente para consulta (doceava edición)
Material recomendado
•Di Pietro, Donato (1985). Geometría Descriptiva. Editorial Alsina. Buenos Aires.
•Izquierdo Asensi, F (1957). Geometría Descriptiva. Editorial Paraninfo. Madrid.
Imágenes de autoría propia, realizadas mediante el programa SketchUp 8 y posteriormente editadas con Microsoft PowerPoint.
Ing. Angel Contreras
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having used the steemstem.io app and included @steemstem in the list of beneficiaries of this post. This granted you a stronger support from SteemSTEM.
Thanks for the support #steemstem #stem-espanol
Congratulations @acont! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Vote for @Steemitboard as a witness to get one more award and increased upvotes!
Thanks @steemitboard
According to the Bible, The Book of Judas: Should You Believe It?
Watch the Video below to know the Answer...
(Sorry for sending this comment. We are not looking for our self profit, our intentions is to preach the words of God in any means possible.)
Comment what you understand of our Youtube Video to receive our full votes. We have 30,000 #SteemPower. It's our little way to Thank you, our beloved friend.
Check our Discord Chat
Join our Official Community: https://steemit.com/created/hive-182074