Math Tutorial
My nephew and neices visited us for the weekend. I love it when they come over, my daughter has playmates, which means she gets entertained while I do the chores in peace.
Tonight, my nephew asked that I teach him some of their math lessons. Honestly, I felt nervous. It's been a long while since I last taught or tutored someone, let alone a kid. I had to do some research first so I could somehow remember the process.
Of course it's one thing to understand math, it's another thing to teach it. To a kid. I am very systematic when it comes to teaching. It's not my profession but when I do teach someone, I wamt to make sure that we end the session with that person learning something - one way or another.
Guaging the Knowledge
So to start, I had to know where my nephew is at. I myself learn that way. I trace back to the topic that I understand then slowly tread my way forward.
I felt it's not enough that I ask him if he knows this or that. He might just say he knows it even if he still has some questions aboutnthat topic. So I went ahead and do a short quiz.
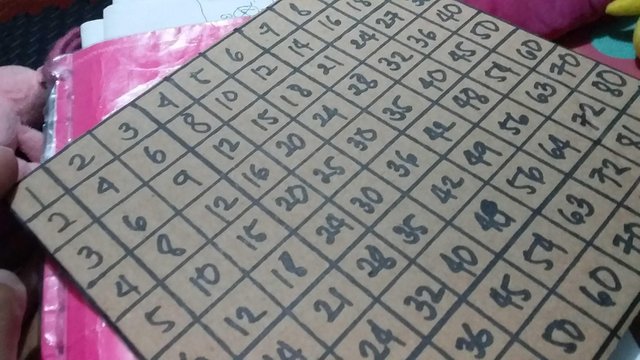
Our topic was reducing fraction to the lowest term. The requisite for that is the greatest common factor. So I had to make sure that he knows how to factor. I also had to make sure that he knows what a factor is. I am sure he knows how to do multiplication and division and skip counting but I made a quick review nonetheless.
Meticulous explanation
I gave him a one by one, step by step process of how to reduce the fraction to its lowest term. Since I am teaching a kid, I had to makenit interesting. Hence the drawings and the arrows and the circles and stuff.
Even at work, when I was mentoring trainees, I teach them the long and tedous process first just so they understand how it works. When I am confident that they already understand the logic behind it, I let them in on the short cuts. That way, they will appreciate the automations more.
Simplify
To a kid, it is easier when you give them a simple view of things. So after I gave him the boring explanation, I gave him a 1-2-3 step combo for the process.
I love how his eyes lit up while he was answering the questions on his own. We started with his eyebrows almost already meeting each other, we ended the session with him smiling.
Give tips and tricks
I did give him some advance lessons so he won't get left behind in class. But the best tip I gave him is that he should never be shy to tell his teacher that he needs more examples or more explanations.
When I younger, some of the teachers I met almost always scolds students who seem to not understand their lessons. It always felt as if it's a mortal sin to ask questions in the class. If you did not understand the lecture, it's as if there is something wrong with you.
But the point of going to school is learning things you didn't know. So before we ended our session, I told my nephew that he should study his lessons in advance so he could understand it beforehand. Learning is a responsibility both of the teacher and the student. If he has questions, he should not hesitate to raise his hand and throw those questions to his teachers. There are no stupid questions. It would only be a stupid question if you did not ask it.





A quote from Calvin and Hobbes, thanks to 3Blue1Brown's YouTube channel on linear algebra for introducing this to me :)
Most of the times maths are indeed taught like that in schools...you memorize the formula, apply it, and see the miracle, and you believe in it. That's not how mathematics work, they are there to solve real world problems, but too bad some of them are just hard to be visualized or have easy examples.
When I saw that drawing on multiplication, it reminded me on how the cross product thingy in vector calculus looks like. Yeah, it sounds like rocket science, but the visualization of the thing is just taking two lines, add two more lines at their ends to make a square (or most of the times, a parallelogram), and find its area, which is exactly as how people multiply numbers. Isn't that multiplication is denoted as a cross? Rocket science.
A good explanation goes a very long way and I'm indeed happy to come over this post...it's really relieving to see that maths is still taught like this and let the students experience the miracle instead of just seeing it. It really makes a very big difference.
Have a nice day :)
I love the quote. I'm not sure though if my nephew would be able to remember everything. Though he was able to solve all the problems I gave him to practice on. I'm not that concerned with his grades though. He is. That's why I told him those are just bunch of numbers. He should enjoy his childhood.
Thanks for taking time to read my blog. :)
Each child learns at different paces and has different learning preferences/styles. I remember when I was a student myself, there were lessons I would understand thoroughly only after the quarterly exams and the topic wont be discussed again until the next year 😅 Hence, now a parent we decided to homeschool our son and give him exclusive learning. It's tough to teach, but we're somehow managing and we're now on our 2nd year.
Posted using Partiko Android
Good for you helping him out! Math can be tricky for some kids for sure.
We homeschool, so I know how that is. The moment when they have their 'AHA!' and everything clicks is amazing. The trick is being able to break it down to where they understand and it makes sense to them. Its more than just memorizing a formula, if you want it to stick, they have to understand WHY they are doing it.
Darn it, I just realized this is an old post. Ill go find a new one to upvote! Happy weekend!