Digital Logic and Boolean Algebra: Can Computers Think?

This article was published on my blog for an introductory course on Information Technology on March 3, 2017.

[Photo source: http://www.learnabout-electronics.org/Digital/dig20.php]

We have been learning about computers in IT 1 – their physical components, i.e. hardware, the operating system, which allows us to interact with the computer, a different OS – Ubuntu, how computers represent data using number systems, and how they compute using binary arithmetic. Now, we are going to explore further how computers ‘think’ and make decisions.

ARE COMPUTERS INTELLIGENT?

In 1950, Alan Turing, who is now known as the Father of the Modern Computer (Copeland & Proudfoot, n.d.), wrote a paper entitled “Computing Machinery and Intelligence” where he asked the question whether computers were as intelligent as humans. This gave rise to the “Turing Test”- a test in which a human must be able to determine which is a real human being from an ‘intelligent’ computer by means of conversing with each of them. If a computer passes this test, i.e. successfully fools a human that it is a human being too, then it probably is intelligent. (TED-Ed, 2016).

We now live in the computer/digital age or the information age. The human civilization has been affected by technology and has become dependent on it to carry out important tasks necessary for its welfare and continued existence. Because of the vast influence of technology and modern computers on every aspect of our lives, it is easy to think that maybe, computers are intelligent to be able to do complex tasks with such speed, efficiency, and accuracy. However, this is a common misconception.

As stated by our laboratory instructor during last Tuesday’s lab session, computers aren’t as intelligent as we think they are. This is because computers are not able to ‘think’ for themselves nor make decisions on their own – they’re only capable of doing exactly what they’re told to do. In this blog post, you will learn that computers aren’t really intelligent, they’re just good at mimicking.

WELCOME TO DIGITAL LOGIC AND BOOLEAN ALGEBRA.

LOGIC.
Cambridge dictionary (n.d.) defines logic as “a particular way of thinking, especially one that is reasonable and based on good judgment”. Basically, it says that logic is a system of thinking that enables one to make decisions. Computers have their system of ‘thinking’ too. It’s called digital logic.

DIGITAL LOGIC.
The foundation of modern computers is digital logic. How it makes complicated decisions by simple two values, yes or no, zero or one, true or false, is governed by this set of rules. (SFUptownMaker, n.d.) Sound familiar? Yes, it’s binary. Two numbers, 0 and 1 are what the computer uses to represent data and perform its tasks.

The CPU, as we’ve already discussed in another blog post, is the brain of the computer. We can also refer to it as the processor or the microprocessor, because it performs control, logical, and arithmetic operations (Albacea, 2007). It is made up of gates, aka ‘logic gates’, which are tiny computers that perform single operations. These gates are then composed of transistors.Transistors are the building block of microprocessors because they act as switches that stop or start the flow of electricity, thus representing 0 for OFF and 1 for ON.

Basically, digital logic is a means to process information by performing mathematical operations and produce an output in the form of 0’s and 1’s. In order to process or evaluate the inputs, we will have to become familiar with Boolean Algebra.

Boolean Algebra

Boolean algebra is the mathematics of manipulating variables which have two values, i.e. 0, the Boolean value false, or 1, the Boolean value true. As we will see, some of the rules of Boolean algebra are different from that of the algebra we’ve learned in high school and introductory college courses; thus, we need specialized expressions for representing them – Boolean functions. These are expressions that are particularly used for binary variables and Boolean operators. Three methods of representations are available: truth tables, algebraic functions, and symbol/logic gates diagram.

Some rules:

0+0=0. 0•0=0. 0’= 1

0+1=1. 0•1=0. 1’= 0

1+1=1. 1•1=1

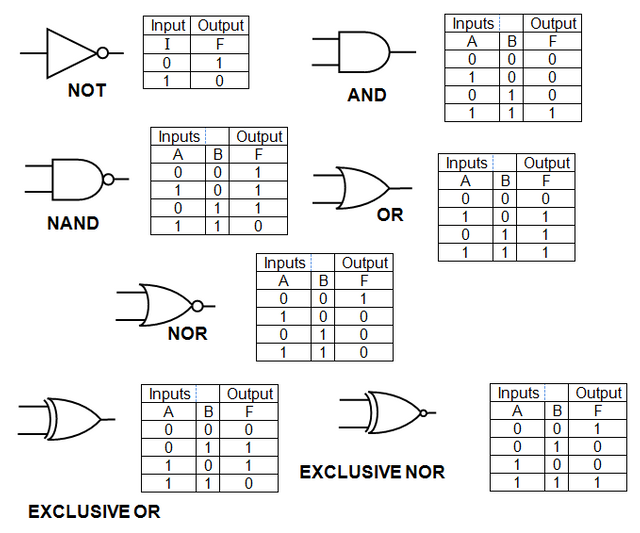
Logic gates

Logic gates perform certain operations whose outputs are 0 or 1. We have 7 of them:

1. NOT gate – This ‘negates’ or gives the inverse of the value of the variable. If we have 1, it becomes 0 and vice versa.

F=x’

1. AND gate – This is ‘conjunction’; it requires that both statements be true for the output to be true, e.g. values from two variables must be 1 to get an output of 1.

F=x•y

1. OR gate – This one is ‘disjunction’; if at least one of the two variables are true, then the output is true. That is, if one of the two variables is 1, then tge output is 1.

F=x+y

1. NOR gate – This is “NOT OR” gate; what it does is it gets the OR output and then negates it. If I have 0 and 1, the OR output is 1. The NOR output turns it into 0.

F=(x+y)’

1. NAND gate – this is ‘NOT AND’; it negates the output of an AND operation. If I have 0 and 1 and the output is 0, I get 1.

F=(x•y)’

1. XOR gate – This gate is an exclusive OR. It requires that only one of the input variables be 1 for the output to be 1. If have I have 1 and 1, then I get 0.

F=xy’+x’y

1. XNOR gate – what this does is that it considers two variables with the same values, i.e. 0 and 0, and 1 and 1. If these conditions are met, then I get 1.

F=xy+x’y’

Basically, the foundational gates are AND, OR, and NOT, while the NOR, NAND, XOR, and XNOR are hybrids of those.

In evaluating gates, we simply follow the rules aforementioned. The rules I wrote before the gates are actually the postulates for conjunction, disjunction, and negation. A postylate is a basic assumption that is accepted without proof. (Albacea, 2007)

To make thing simpler, we can also construct a truth table. The number of rows is = 2^n, where n=number of variables we have. Thus, for F = x+y’z, we have:

2^3 = 8 rows

Basically, we just list the 0’s and 1’s for each column corresponding to a variable then writing the corresponding outputs for F.

We can also prove expressions, i.e. shorten them. We use these theorems:
Identity

A•1=A A+0=A

Inverse

A•A’=0. A+A’=1

Commutative

AB=BA. A+B=B+A

Distributive

A(B+C)=AB + AC

A+(BC) = (A+B)(A+C)

Absorption

A+AB =A. A(A+B)=A

De Morgan’s Law

(AB)’=A’+B’. (A+B)’=A’B’

Contra-identity/Null

A•0=0. A+1=1

Double negation/Involution

A”=A

Associative

A(BC)=(AB)C

A+(B+C)=(A+B)+C

Idempotency

AA=A. A+A=A

Expansion

AB+AB’=A. (A+B)(A+B’)=A

Logic circuit and truth table for each logic gate from http://www.schoolphysics.co.uk/age16-19/Electronics/Logic%20gates/text/Logic_gates/index.html

The computer, which most of us view as seemingly mysterious and complicated, turns out that it is not as complicated as we think. It uses simple mathematical operations in making its decisions and can only distinguish between two states, ON or OFF, TRUE or FALSE, using only two values, 0 or 1.

So, can computers think? The answer is no. They cannot think and make decisions on their own, they can only follow orders exactly as they’re instructed to. And these logic gates are what they use in making decisions based on given values.

References

Albacea, E.A. (2007). Information Technology Literacy, 4th ed. JPVA Publishing House, Quezon City.

Copeland, B.J. & Proudfoot, D. (n.d.). Turing, Father of the Modern Computer. Retrieved from http://www.rutherfordjournal.org/article040101.html

Logic [Def. 1]. (n.d.). Cambridge Dictionary. Retrieved, from http://dictionary.cambridge.org/dictionary/english/logic

SFUptownMaker. (n.d.). Digital Logic. Retrieved from https://learn.sparkfun.com/tutorials/digital-logic

TED-Ed. [TED-Ed]. (2016, April 25). The Turing test: Can a computer pass for a human? – Alex Gendle. [Video File]. Retrieved from