La incorporación del Arte y el Diseño en el maravilloso e infinito mundo de las Matemáticas
¡Hola! Lectores bonitos y coloridos

Fuente
El post de día de hoy, ufff...es algo diferente, que en lo personal siento que les impactara porque muchos piensan que el diseño y el arte no tienen relación. Hoy por acá, les subo una investigación realizada por mi persona. Sigan bajando un poquito y disfruten de este articulo científico...abran su mente, su creatividad a volar!.


Durante muchos años, en la sociedad ha sido muy común la sistematización de cada una de las áreas; haciendo que por lo general las personas crean una idea errada de que las matemáticas y el arte/diseño no tengan ningún tipo de vinculación y viceversa. No obstante, en la actualidad con la intervención del internet y su uso cada día más indispensable en nuestras vidas, hemos descubierto un millón de cosas y entre ellas la veracidad de las cosas; tomando la idea anterior, se puede notar que las matemáticas han estado involucradas prácticamente en todo lo que es relacionado con cualquier avance en cualquier sistema, haciendo que cada día sean mas indispensables en nuestras vidas y mas aun si hablamos de algún invento o innovación.

Fuente: pearlinux.fr
Ahora bien, El arte y las matemáticas han estado estrechamente unidos a lo largo de la historia. El popular número dorado que habíamos hablado en un post anterior, click aquí para más… que fascinó a Leonardo da Vinci, la búsqueda de la fórmula matemática de la belleza y los trabajos de Escher; son tres conocidos ejemplos, pero además las matemáticas tienen mucho que ver con el cine, el arte contemporáneo, la pintura, la fotografía y, por supuesto, con el llamado octavo arte: los videojuegos.

Fuente: Blog PIENSA Y RESUELVE
Continuando la idea anterior, podemos añadir un bicondicional (como en las matemáticas discretas) para lo planteado; así como las Matemáticas han sido fundamentales para los avances en cualquier ámbito, ejemplo: en el arte y el diseño…esto permite aplicar que, El arte y el diseño también es condicional para que las matemáticas avancen y hasta sean más fáciles de entender para quienes quieren navegar en el mundo infinito de los números. (Si lo sé, suena muy romántico).
¿Sabias que…? Según el espacio en la web de www.muyinteresante.es ‘’El nuevo MathsLAB es el único espacio estable del mundo que aborda la relación entre arte, creatividad y matemáticas. Según sus creadores, si bien muchos museos de ciencias dedican actividades puntuales a las matemáticas, o se han celebrado exposiciones que muestran las conexiones entre ambas disciplinas, sólo hay un antecedente: Mathematikum, un centro dedicado expresamente a las matemáticas, situado en la localidad alemana de Giesse, a 60 kilómetros al norte de Frankfurt. Sin embargo, su objetivo principal es divulgar, a través de conferencias, exposiciones y actividades especiales durante los fines de semana, los fundamentos de esta ciencia y su relación con el arte.’’
Por otra parte, La mayoría de diseños, obras de arte, arquitectura, objetos o incluso personas estéticamente agradables se rigen por una proporción matemática. Lo cual habíamos hablando en un post anterior. Si bien cierto, las matemáticas nos proporcionan infinitas variables, formulaciones y teoremas para plantearnos una idea y de ahi una solución. Ahora, cuando tomamos en cuenta el uso de la geométrica; los fractales son secuencias matemáticas en los cuales se repiten patrones geométricos que se combinan para formar un todo. En la naturaleza, los fractales constituyen hojas, copos de nieve, las estructuras geológicas y cristales de hielo. ¿Un ejemplo más a la mano? Corta una naranja y veras como la forma de la pulpa es un patrón de repetición.

Fuente
Añadiendo a lo anterior, se puede observar en la imagen de referencia que, nuestras células forman fractales de repetición. Por ello, los científicos usan fórmulas matemáticas para crear modelos de casi cualquier cosa basado en fractales. Todo lo que necesitan saber es la forma del fractal en el nivel más pequeño y luego conseguir que fractal multiplicar. Ahora lo interesante de esto y lo aplicable es que en diseño, los fractales se utilizan para varias aplicaciones como diseño de ropa o fondos en páginas web, sólo por mencionar algunos, lo cual se llama Patrones.
 Fuente
Fuente Con respecto al bicondicional que había planteado anteriormente, la influencia del diseño en el estudio de las matemáticas; es muy romántico e interesante, debido a que, cuando se utiliza el potencial de la creatividad en función a la necesidad gráfica matemática, podemos encontrar maravillas de las herramientas artísticas que existen para el avance del estudio y entendimiento de las matemáticas.
Ahora bien, en la sociedad existe la idea errada de que la vinculación de estas dos áreas es inadecuada, al contrario, plantear ideas gráficas que faciliten el estudio de los números, nos permite incluso imaginar con facilidad la idea matemática e internalizar soluciones para formulas matemáticas y en consecuencia entender el mundo de los infinitos números.
- Por ejemplo, una de las herramientas más funcionales para el estudio de las matemáticas y su representación es; GeoGebra definido por www.geogebra.org como ‘’ Un Software matemática, el cual, básicamente es un procesador geométrico y un procesador algebraico, es decir, un compendio de matemática con software interactivo que reúne geometría, álgebra, estadística y cálculo, por lo que puede ser usado también en física, proyecciones comerciales, estimaciones de decisión estratégica y otras disciplinas. GeoGebra permite el trazado dinámico de construcciones geométricas de todo tipo así como la representación gráfica, el tratamiento algebraico y el cálculo de funciones reales de variable real, sus derivadas, integrales, etc’’.
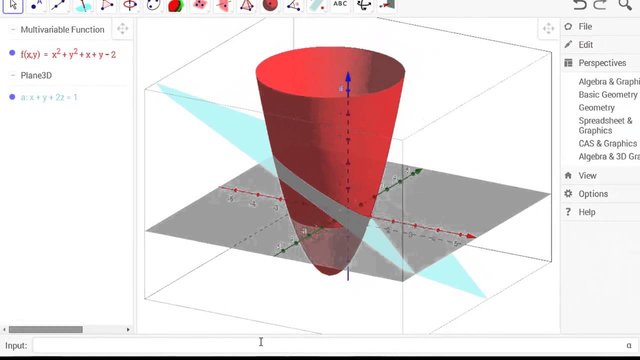 Fuente: Captura desde mi laptop de un video de Youtube
Fuente: Captura desde mi laptop de un video de Youtube Entonces, tomando en cuenta el ejemplo anterior, podemos tomar como referencia y afirmar que el diseño grafico e incluso el arte permite evolucionar en el mundo matemático, así generando avances que incluso a nivel educativo escolar o universitario es beneficioso para el entendimiento de aquellos que estudien los números. Añadiendo que un buen diseño artístico, explosivo en todo su potencial creativo siempre será adecuado para generar un impacto atractivo y as ocasionar interés, incluso en aquellos que les da miedo aprender de los números.
Siguiendo la idea anterior, Todos sabemos que no siempre las matematicas son comprensible. A veces nos cuesta entender un concepto, o el significado de una ecuación y entonces con una imagen, simplemente con una ilustración, entendemos el verdadero significado de las palabras. Si queremos por ejemplo, explicar la presencia de las matemáticas en la naturaleza, como es el caso del número phi, si damos la definición. Phi es un número irracional, φ =1.618033988749895…, que representa la proporción áurea o el llamado número de oro, y que es una razón definida por la siguiente construcción geométrica, con su ecuación asociada:
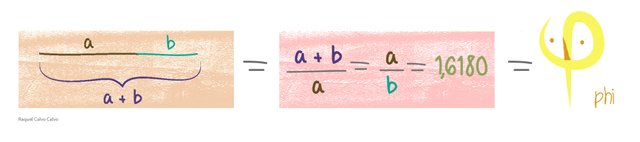 Fuente
Fuente Por ultimo, con la belleza de estas dos constantes, que son bellas por estar en la Naturaleza, le dejo una cita del matemático Godfrey Harold Hardy que habla de la belleza de las matemáticas, dice así:
''Un matemático, como un pintor o un poeta. Es un fabricante de modelos. Si sus modelos son más duraderos que los de estos últimos, es debido a que está hechas de ideas. Los modelos del matemático, como los del pintor o los del poeta deben ser hermosos. La belleza es la primera prueba; no hay lugar permanente en el mundo para unas matemáticas feas.''
Entonces, la Naturaleza y la belleza van unidas. La armonía que hay en sus patrones matemáticos, en sus constantes como el número phi, la geometría o las gráficas, todo esto hubiese sido mucho más difícil explicarlo sin imágenes ilustrativas.

Referencias
- Lawlor, Robert: "Sacred Geometry. Philosophy and Practice", Thames and Hudson, 1982, ISBN 0-500-81030-3.
- H. Hardy. (1999). Apología de un matemático. Editorial Nivola.
- Blog y Revista MasScience
- Blog Paredro- La Perfecta Influencia de las Matemáticas en el DiseñoPor Redacción Paredro octubre 19, 2015

Quiero recordarles que si quieren sus post super cool e innovadores, el toque esta en los Gifs. Les dejo aca abajito el link donde pueden conseguir gifs perfectos para cada temática.
También invitarlos a mi nuevo proyecto personal y laboral, mi nueva pagina WEB de diseño gráfico. Donde publico mis proyectos y productos.
Antes de despedirme, pedirles el mega favor de dejarme acá abajito sus comentarios y preguntas. Estaría super cool interactuar sobre la información. Gracias por leerme. Hasta mi próximo reportaje. Un besote virtual!
upvote for me please? https://steemit.com/news/@bible.com/6h36cq