Excitaciones y defectos

¿Te acordás de estos cables? Todos los que nacimos en el siglo XX hemos tenido que lidiar alguna vez con ellos

(Own collection)

Para los púberes: es el cable de un teléfono fijo, la forma espiral sirve para poderlo estirar con facilidad, alejándolo de la base.

Si sostenemos un cable de ese tipo, suavemente estirado entre nuestras manos, la espiral será mas o menos regular a lo largo de él. Si la comprimimos ligeramente en algún punto, hacemos lo que se llama una deformación local. Al soltarla, la deformación local se relaja, moviendose a lo largo del cable, y el punto donde habíamos comprimido vuelve a su posición inicial. Todo esto pasa sin necesidad de que soltemos los extremos del cable. En otras palabras, esta deformación local se puede deshacer localmente.

Llamamos una excitación elemental del cable a tal deformación local que se puede deshacer localmente. Si pulsamos el cable como la cuerda de una guitarra, se crean muchas de tales excitaciones elementales que se mueven a lo largo de él.

Sin embargo, hay otro tipo de situaciones que se pueden producir en un cable de este tipo: el enredo o rulo. Podemos verlo en la siguiente foto:

(Own collection)

Este tipo de deformación no se deshace sola.
La única forma de deshacerla es llevando el rulo hasta la punta del cable, y luego soltando ese extremo. En otras palabras, es una deformación local que no se puede deshacer localmente. Se trata de un defecto topológico.

Este tipo particular de defecto topológico puede viajar a lo largo del cable. En ese caso, lo llamamos excitación solitónica o equivalentemente solitón.

Así como las ondas se pueden asociar a las partículas a través de la dualidad onda-partícula, lo mismo sucede con los solitones. Para entender esto, examinemos el rulo en el cable de teléfono. Vemos que el cable está tensionado en el punto donde se localiza el defecto. En otras palabras, el rulo contiene una concentración de energía en ese punto. Esta concentración de energía es indistinguible de una partícula, y no hay razón para negarle al solitón tal estatus.

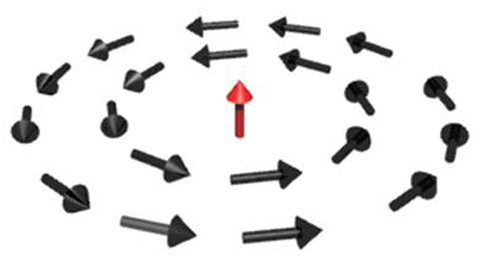
Hay muchos otros casos de excitaciones solitónicas en sistemas físicos. Yendo a un ejemplo un poco más técnico, esto es un espín flip:

Fuente

Las flechitas representan la cantidad de rotación (el "espín") de cada uno de los átomos a lo largo de una molécula de un polímero, que tiene la forma de una larga cadena unidimensional. Podemos imaginarnos las puntas de cualquier par de flechitas sucesivas unidas por bandas elásticas, representando así las fuerzas entre los distintos átomos. Si quisiéramos desatar el nudo, al dar vuelta la flechita donde se encuentra el defecto, la banda elástica nos obligaría a dar vuelta la siguiente, y luego otra más, y así hasta llegar a la punta de la molécula. De nuevo, la configuración local no se puede desarmar linealmente, se trata de un defecto topológico.

Como este defecto se puede mover a lo largo de la molécula, estamos ante un solitón. La energía está concentrada en el lugar donde está la banda elástica más estirada, es decir en el defecto. Por esta razón, podemos considerarlo con todo derecho una partícula.

Tanto el cable como la molécula son objetos unidimensionales. Luego tanto sus excitaciones elementales cuanto las solitónicas se moverán en una dimensión. Pero este tipo de fenómenos existen también en dimensiones mayores.

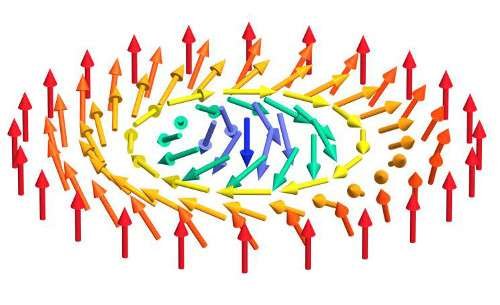
En un plano, es decir en dos dimensiones, podemos tener exitaciones solitonicas. Por ejemplo, esto es un eskirmión:

Fuente

Las flechitas como antes representan el espín, ahora de un material en forma de capa bidimensional. De nuevo, la interacción entre los átomos contiguos se puede imaginar como bandas elásticas entre las puntas de las flechitas. La flechita del centro mira hacia abajo, las del exterior hacia arriba. Si quisiéramos desarmar la configuración dando vuelta la flechita del centro, las bandas elásticas nos obligarían a girar las flechitas que la rodean, y éstas moverían las más alejadas, y así hasta llegar al borde. De nuevo, la deformación local no se puede deshacer localmente: se trata de un defecto topológico.

Este defecto topológico se puede mover, por lo que es una excitación solitónica. La excitación contiene energía concentrada en el lugar donde las bandas elásticas están más estiradas, es decir cerca de la flechita del centro. Por lo tanto, hay una concentración de energía en un punto, de nuevo asimilable a una partícula.

Similar al anterior es el llamado vórtice:

Fuente

Se trata de una estructura con propiedades análogas casi en todo al eskirmión, sólo cambia el modo en el que se disponen las flechitas.

Estos dos tipos de defectos topológicos aparecen en los materiales cerámicos superconductores. Su comprensión será la clave de una revolución tecnológica en ciernes, ya que permitiría obtener superconductividad a temperatura ambiente.

Sin embargo, en dos dimensiones hay lugar otro tipo de defectos topológicos, conocidos como paredes de dominio. Como su nombre lo indica, se trata de una pared, es decir una línea tal que a un lado de ella todas las flechitas apuntan hacia arriba, y al otro lado todas apuntan hacia abajo. En este caso la concentración de energía no está en un punto, sino todo a lo largo de la pared. Es decir que este solitón no se puede interpretar como una partícula, sino más bien como un objeto extendido unidimensional.

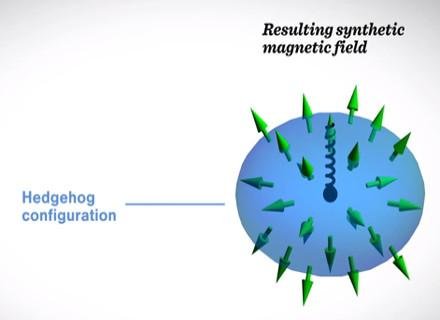
¿Y qué sucede en tres dimensiones? Imaginemos ahora que el espacio tridimensional está lleno de flechitas. Si estamos dentro de un material podrían representar el espín de los átomos constituyentes, como en los ejemplos de más arriba, aunque también se las usa a veces para representar algo más exótico como el campo de Higgs. Lo importante es que en cada punto tienen que apuntar en alguna dirección. Esta configuración que vemos aquí es un monopolo magnético:

Fuente

Las flechitas se acomodan como un erizo que se aleja de un centro común. En ese centro habrá una concentración de energía, por lo que podemos interpretar este solitón como una partícula. Este tipo de solitones se comporta como un imán con un solo polo, de ahí su nombre. En los materiales, estas configuraciones resultan fundamentales para explicar algunas transiciones de fase. En el caso del Higgs, no hemos encontrado aún tales monopolos, pero su existencia nos diría mucho acerca del comportamiento de la materia a nivel fundamental.

Pero tres dimensiones tenemos más posibilidades. Podríamos tomar las configuraciones de eskirmión o de vórtice y apilarlas para formar una estructura tridimensional. De este modo, obtendríamos una configuración posible de las flechitas en tres dimensiones. Esta configuración tendría su energía concentrada en un hilo, a lo largo del cual están apilados los centros de cada uno de los vórtices. Ese hilo se llama cuerda cósmica y juega un rol importante en la cosmología moderna.

O podríamos apilar en cambio paredes de dominio. Entonces la energía estaría distribuida en una membrana, formada por las líneas apiladas de cada pared de dominio. Esta membrana es otro tipo de excitación solitónica posible en tres dimensiones. En el caso de los materiales, tales membranas proliferan dentro de un imán viejo, y por eso pierde su imantación.

En física teórica, resulta natural considerar al tiempo como una dimensión adicional del espacio tiempo, el cual tiene entonces cuatro dimensiones. Resulta natural entonces preguntarse ¿hay defectos topológicos localizados en un punto en las cuatro dimensiones del espacio tiempo? Se trataría de un objeto cuya energía estaría concentreada en un punto del espacio durante un instante. Es decir, existiría solo durante un efímero click. Tal configuración de instantón en efecto existe, como un chasquido que aparece en los procesos cuánticos en los cuales se produce efecto túnel.

En teoría de cuerdas, la cual creemos que explica los fundamentos de la física, el espacio-tiempo no tiene cuatro dimensiones, sino diez. En ese caso, la mayor dimensionalidad permite una plétora de excitaciones solitónicas con la forma de objetos extendidos: instantones, monopolos, cuerdas cósmicas, membranas, y p-branas, es decir objetos extendidos de p dimensiones. Uno de los modelos cosmológicos más reputados del presente propone que nuestro universo es en realidad un solitón cuadridimensional en un mundo decadimensional.

¿Cómo se forman los defectos topológicos? Por efecto dominó, algo que en física se conoce como mecanismo de Kibble, por Tom W. B. Kibble.

Imaginemos una fila de fichas de dominó. Alguien la empuja en una punta originando una ola de fichas que van cayendo. Otra persona hace lo mismo en la otra punta. Eventualmente las dos olas se encuentran. En el punto de encuentro las dos olas "se traban", formando una configuración que no se puede deshacer localmente. O sea un solitón. Si acomodamos varias filas de fichas sobre una mesa y le damos un golpe, indefectiblemente se formarán varias de esas olas que se trabarán al chocar entre sí, creando solitones.

Los defectos topológicos fueron uno de los temas álgidos de física en los 70's y 80's, y hoy generan infinidad de ideas en áreas de frontera de física teórica. En lo perfonal, me resultan uno de los temas mas interesantes y ricos.

Mis posts se publican en

• Cave Canem (ciencia, opinión)
• Literatops (literatura, citas literarias)
• Diaspora*
• Mastodon
• SteemIt
• Reddit
• Facebook
• Telegram
• Tumblr

También me pueden contactar en

• XMPP @severianx@xabber.org
• XMPP @severian@despora.de
• Discord @SeverianX#6874
• SteemChat @SeverianX
• CuriousCat
• e-mail