La Simetría Dimensional: ¿Y Cómo Explorar el Vacío?

    Empecemos entonces –decíamos–, por entender, ya no el qué estudiar, sino el por dónde y cómo entrar en el estudio del espacio en geografía. Esto es, por dónde y cómo entrar en el estudio del vacuum, determinado, para empezar, por la esfera terrestre; o, inversamente dicho para más precisión, cuyo espacio y su estructura determina la esfera terrestre con todos sus fenómenos; a manera de cómo no es el diamante el que determina la estructura cristalina, sino, inversamente, donde es la estructura cristalina la que detrmina el diamante.

     Así, todo empezó por observar una superficie terrestre con la distribución en un hemisferio de agua, y un hemisferio continental; de una cuenca del Mar Ártico en el Polo Norte, y un continente antártico en el Polo Sur, que, además se corresponden en su forma y magnitudes de superficie y volumen; de una deriva continental que tiende a la convergencia de las masas terrestres hacia la cuenca del Mar Ártico en el Polo Norte, haciendo el efecto de un toroide; de esa curiosa terminación en vértices triangulares de América del Sur, de África, y de la India; asociando esa situación geográfica empírica extraña, con la simetría dimensional triaxial de la esfera terrestre. Todo ello ha sido desde siempre objeto de curiosidad a la observación humana; ello no es, evidentemente, un asunto de la geología, ni de la geodesia o geofísica, e intuitivamente, en el sentido común, se había dejado su explicación a la geografía, sin que ésta lo hiciera tampoco debido tanto a que su objeto de estudio no se definía por el espacio, como, porque, en consecuencia, la mayoría de los geógrafos habían estado ocupados por siglos en hacer “geología” o “geofísica”, disfrazada de “geografía aplicada” a los fenómenos geológicos o geofísicos.

     De dicha simetría dimensional triaxial de la esfera terrestre, se hace natural a la observación la existencia de un eje de simetría polar (z) que aparece de forma objetiva en un Hemisferio Norte y un Hemisferio Sur; pero el primer problema que se planteaba a esta teoría, es que los dos ejes restantes no parecían poder determinarse de la misma manera objetiva. Sin embargo, pronto, ya ocupados en ello metódicamente, observamos que un eje más (y), bien podría corresponder a los puntos diametralmente opuestos entre el centro del Océano Pacífico, 0º𝜑-160º𝛌W (en el hemisferio de agua), y su correspondiente a 180º en África, 0º𝜑-20º𝛌E, al oeste de Gabón, a unos 130 km del Río Congo (en el hemisferio continental); por lo que, de manera geométrica por la perpendicular a él, se tendría el eje (x) entre los puntos diametralmente opuestos de 0º𝜑-70º𝛌W (prácticamente en la convergencia fronteriza de Ecuador, Colombia y Perú), y 0º𝜑-110º𝛌E (frente a Singapur, en dirección de la Península de Malasia), puntos por donde corta el plano de división entre esos hemisferios de agua y de continentes; y por lo tanto, encontramos que tales ejes podían determinarse, a su vez, objetivamente.

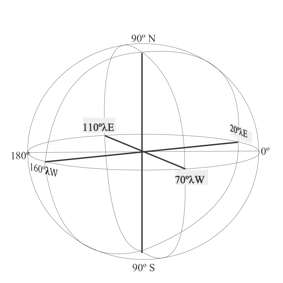
     La base rígida de la simetría dimensional había sido echada, todo lo demás sería, en función de ella como causalidad, el dar explicación a todos esos efectos de movimiento y distribución, ya no sólo en la superficie terrestre, sino en toda la estructura del espacio planetario desde su interior hasta la magnetósfera.

     Determinado así, la simetría dimensional (tridimensional o triaxial) de la esfera terrestre nos da la métrica del espacio objetivo de propiedades continuas (espacio vacío), que establece una relación causal evidente sobre la estructura espacial de propiedades a su vez tanto continuas (como en los diversos campos, térmico, barométrico, lumínico, electromagnético), como discretas (la litósfera, la atmósfera, la hidrósfera, la biósfera, la sociósfera); es decir, con efectos en los diversos estados de espacio (espacios plenistas).

     Desafortunadamente, así como perdimos la fecha de aquel día del “¡Eureka!” de 1981 en que nos dimos cuenta que el objeto de estudio de la geografía era el espacio, así también se nos escapa la referencia de en qué momento comenzamos a formalizar la analogía del estudio del espacio con la cristalografía. Desde la infancia ya podíamos ver el Universo en aquellas canicas que llamábamos “agüitas”, transparentes, de colores, en particular las azules, que cuantas más pequeñas burbujas de diversos tamaños tuviesen encerradas a manera de “galaxias”, mejor al vuelo de la imaginación. La misma imagen nos formamos, quizá hacia el año 2005, pensando en la manera de empezar a estudiar el espacio como tal; y siendo la canica lo que mal llamamos en un principio como un “cristal” cuando es un vidrio, algún impreciso día recurrimos a la teoría de la cristalografía para ver si con ello nos dábamos una idea, sin imaginarnos que ahí mismo estaba la solución a la teoría del espacio en geografía; pero el lapso de esa formalización teórica, a la vez se nos hizo difuso (entre 2005 y 2007), en mucho, porque por entonces no sólo no estábamos publicando nada, sino ni siquiera escribiendo lo que pensábamos acerca de la geografía teórica.

     Fue hasta 2009 que empezamos otra vez a publicar, ahora mediante un Blog en Internet: http://espacio-geografico.over-blog.es; y primero lo hicimos con todos nuestros trabajos antecedentes hasta llegar, hacia 2011, a lo último que teníamos en ese momento; y allí es cuando ya expusimos la formalización de la analogía, y con ello, a su vez, comenzó la formalización teórica de la teoría que en un principio denominamos como “geometría de simetría dimensional”, pero que pronto redujimos simplemente a “teoría de simetría dimensional”.

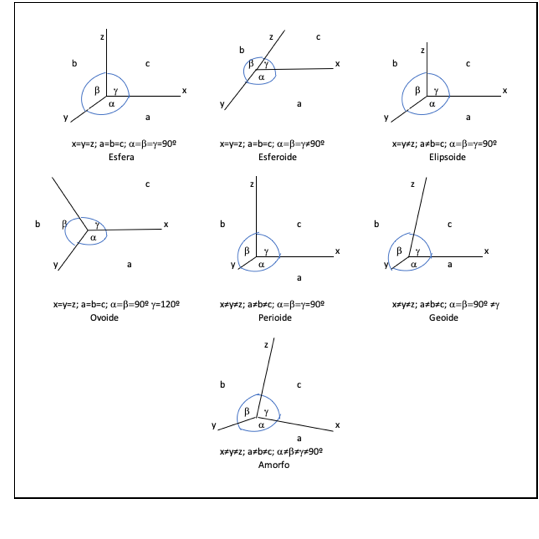
     La estructura del espacio no sólo la deducíamos de una geometría euclidiana tridimensional que lográbamos acoplar objetivamente a la estructura de la esfera terrestre, sino que, de la obra de Riabchikov, “Estructura y Dinámica de la Esfera Terrestre”, 1969; conocíamos el dato de que los ejes de la Tierra se alargaban o contraían en un rango de hasta 20 cm (con la correspondiente absorción o despido de energía térmica, enorme en correspondencia al volumen de la Tierra no obstante los escasos centímetros). Al estudiar la analogía con la cristalografía, observamos que las leyes de la estructura de los cristales, en la generalización de sus propiedades geométricas, podían trasladarse sin contrariedad a la estructura del espacio terrestre mismo; pero más aún, observamos sin dificultad que en el arreglo de esas estructuras se daba una secuencia de lo absolutamente irregular en un cuerpo amorfo, a lo absolutamente regular en una esfera tendientemente perfecta, sin que, para el caso de la Tierra, pueda alcanzar nunca tal último estado, como consecuencia de los efectos gravitacionales de la Luna en sus movimientos de traslación y de rotación del eje de los nodos; todo lo cual bien correspondía con el proceso evolutivo de la formación de la Tierra.

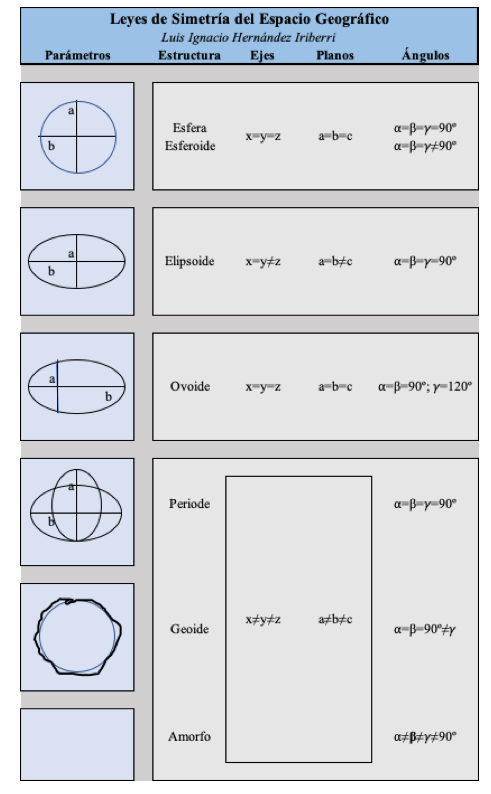
     Y en este punto de nuestros estudios estábamos, cuando de pronto nos encontramos, a mediados de 2012, con el trabajo fundamental de Genadi Nicolaievich Katterfeld (1927-2013), “La Faz de la Tierra y su Origen”, 1962; autor del que sólo teníamos una vaga referencia tomada del mismo A.M. Riábchikov en su obra, en la cual mostraba unos mapamundis de éste en proyección ecuatorial y polar, con una serie de líneas de una evidente simetría determinada por las estructuras orográficas y continentales, pero sin más explicación; y esencial documento de Katterfel que apenas unos tres meses atrás había sido “desclasificado” por la “Agencia Nacional de Aeronáutica y del Espacio” (NASA), de los Estados Unidos, el cual lo había mantenido guardado en secreto por más de cuarenta años; y casi de inmediato, en el curso de ese segundo semestre de 2012, hicimos una serie de artículos explicando el trabajo de Katterfeld y sus aportes, a lo que, curiosa y sorprendentemente, en ese momento la NASA retiró dicha publicación de su sitio en Internet. Luego, en una circunstancia peliculezca (dada entre fines de 2012 y fines de 2016), incluso nos enteramos que ese documento de Katterfel, a su vez, era objeto de alto secreto de Estado en Rusia desde la antigua URSS.

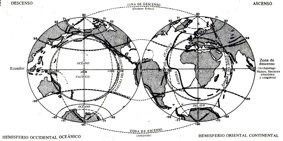
     El hecho es que con esa obra fundamental de Katterfeld, finalmente entendimos lo expuesto en aquellos mapamundis suyos, que, para nuestra sorpresa, era una expresión concreta, descubierta por él desde principios de los años sesenta, de lo que nosotros recién habíamos empezado a hacer. La relación de nuestro trabajo con el de Katterfel es, por una parte, una relación de lo general (nuestra teoría de simetría dimensional) a lo particular (su teoría de la asimetría causal de rotación); pero, por otra parte, una relación inversa en las determinaciones causales generales, en las que mientras que para Katterfel van en particular de las estructuras que él llama morfotectónicas, a la simetría espacial; en nuestro caso, inversamente, es la simetría espacial la determinante de toda otra estructura terrestre.

     Desconocemos lo que tal autor haya hecho después de ese documento más allá de la referencia de los títulos de algunos de sus trabajos, pero más adelante, en subsiguientes artículos, volveremos obligadamente a sus esenciales y fundamentales aportes. Mas, en tanto que esa relación de lo general a lo particular entre ambas teorías, expondremos primero el desarrollo de nuestra teoría de simetría dimensional, que pronto se mezclará y ajustará con la teoría de la asimetría triaxial o causal de rotación de Katterfeld.