La Simetría Dimensional. Las Homologías Geográficas
La Simetría Dimensional.
Las Homologías Geográficas
Luis Ignacio Hernández Iriberri.
[24 may 20]
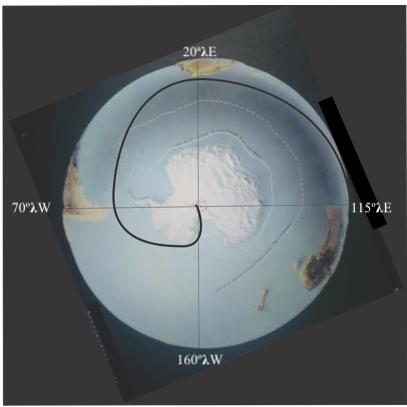
El Capítulo 3 de “La Faz de la Tierra y su Origen” de Katterfel se refiere a lo que el titula como las “Homologías Geográficas”; esto es, a las figuras semejantes opuestas una a la otra, lo que Katterfel califica incluso de “La clave para comprender la distribución de los continentes y océanos”, donde la principal de tales homologías (que nosotros, por más que evidente, no habíamos observado), es la oposición antípoda de los continentes y océanos, es decir, donde las antípodas de los continentes son los océanos, lo cual se observa tomando las tierra continentales, invirtiéndolas y colocándolas en el lugar que corresponde a los océanos; de modo que si los 15º𝛌E se acoplan a los 165º𝛌W en el Océano Pacífico, la parte sur de África ocupa una porción del Pacífico Norte y toda la masa continetal desde África hasta Asia ocupa el Pcífico Sur, en tanto que Australia y Nueva Guinea el centro del Atlántico Norte; e inversamente, si la masa continental de América se lleva invertida a su antípoda, haciendo coincidir los 165º𝛌W con los 15º𝛌E, toda América del Norte abrca el Océano Índico en tanto que América del Sur se corresponde con el conjunto de islas de Indonesia, el Mar de China y y el Mar de las. Filipinas; sólo el extremo sur de América (de Uruguay a Argentina y Chile), se empalama con la región continental de China. Luego se refiere (en la misma observación que nosotros sí ya habíamos hecho), igualmente para el caso de los Casquetes Polares Ártico y Antártico, incluso con sus valores correspondientes de depresión oceánica y altitud continental.
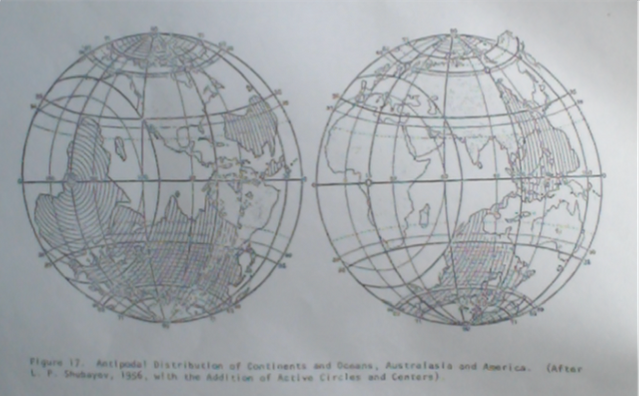
Esta distribución de simetría antípoda (por rotación y reflejo), se produce, dice Katterfeld, como consecuencia de movimientos compensatorios de masas, no sólo en sentido ecuatorial, sino en sentido polar: ecuatorialmente, como se ha visto, como consecuencia de la marea gravitatoria Tierra-Luna; y polarmente como consecuencia, por su parte, de la compresión polar diferenciada en el perioide, mayor en el eje polar norte, y menor en el eje polar sur; proceso mismo que contribuye a la ya analizada rotación diferencial entre los hemisferios norte y sur dada por las diferencias de masa y materiales litológicos dominantes en la corteza terrestre.
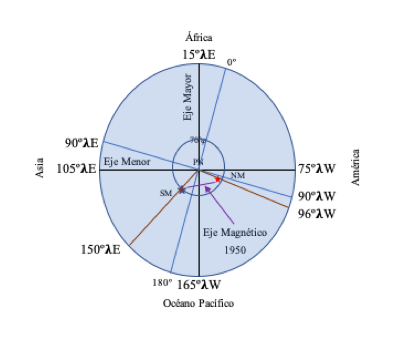
En este mismo capítulo, Katterfeld se refiere brevemente a la “asimetría del campo magnético de la Tierra”, campo magnético (un continuo) al que se refiere dado, a su vez que en la masa terrestre (discreta), en forma de corazón; pero a lo que nosotros nos hemos referido en su estuctura básica como un toroide, que luego, en su estructura secundaria bajo el influjo del “viento solar”, se deforma como la cauda de un cometa. Donde los polos magnéticos con datos de 1950 en Katterfeld, se localizan en los 78º32’𝜑N-69º08’𝛌W, y 78º32’𝜑S-110º52’𝛌E; que proyectados sobre el plano del ecuador, ubica su eje en los 72º𝜑N-96º𝛌W; y, 70º𝜑S-150º𝛌E. Más allá de estos datos, Katterfel no se va a referir más al campo magnético terrestre, poco estudiado aún para fines de los años cincuenta, en que, con motivo del Año Geofísico Internacional en 1957, Van Allen descubre los anillos del campo magnético que llevan su nombre.
En su cuarto y último capítulo, Katterfel trata sobre las “Leyes de la Formación y Distribución de los Cinturones de Montañas” en unas veinte páginas; sin duda un hecho geográfico, pero del que aquí prescindiremos por la particularidad de su tratamiento, cuando que lo que nos ha interesado son los fundamentos generales de su teoría de la “asimetría traxial-causal de rotación”, a la que está estrechamente vinculada hasta aquí nuestra teoría de la “siemtría dimensional”.
Finalmente, entre esas homlogías geográficas está esa primera consideración histórica de las simetrías del espacio geográfico terrestre: las “esfrágidas” de Eratóstenes –de lo que Katterfeld no habla–, lo cual se refiere al por qué los continentes forman vértices triangulares hacia el sur; América; África; Arabia, en este caso como una forma que empezaba a darse; India; e Indonesia, esta última como si se hubiese fragmentado; explicación, por lo tanto, que ya queda por entero en nuestras manos (y realmente a partir de donde se disparó nuestra teoría de la simetría dimensional como fundamento del estudio del espacio geográfico). Dada la extensión del artículo, nos referiremos aquí sólo a sus consideraciones generales, y en un subsiguiente artículo entraremos en su análisis en detalle.
Siguiendo la metodología y razonamientos de Katterfeld, esas formaciones que en honor a Eratóstenes nosotros seguimos denominándolas como “esfrágidas”, tienen sus vértices al sur, en general, y considerando en primer lugar las grandes formaciones, según los siguientes datos:
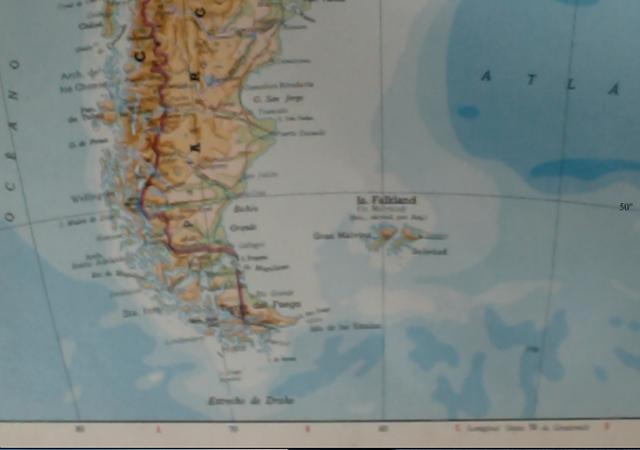
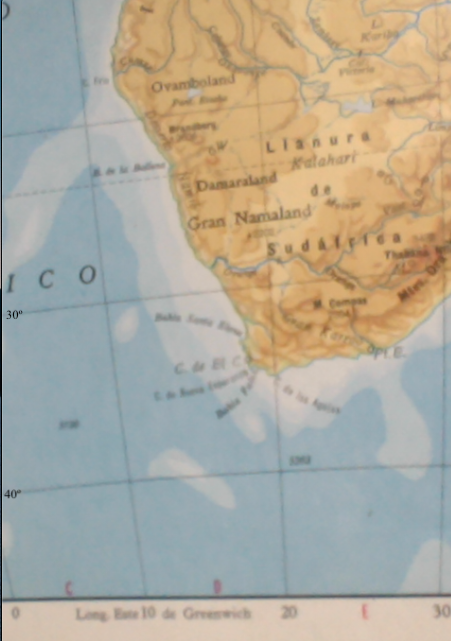
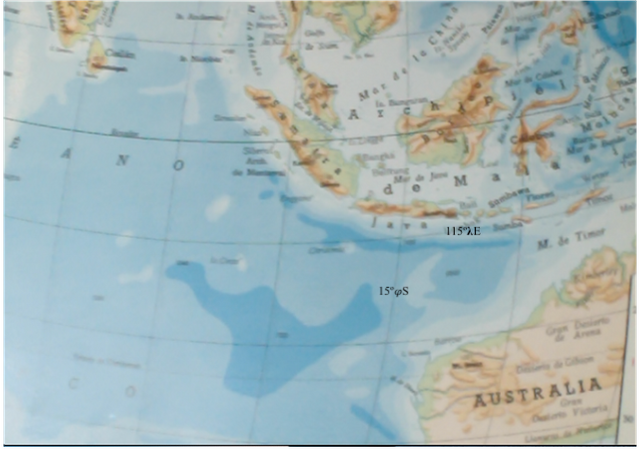
Finalmente, dos hechos homólogos de absoluta y sorprendente simetría se ponen en claro aquí: 1) las latitudes decrecen en un intervalo de 20º, simultáneamente a que; 2) las longitudes corresponden exactamente a los planos meridionales de la estructura básica dimensional de la Tierra, aun cuando no en los ejes o planos de Katterfeld, sino en los que originalmente nosotros habíamos considerado siguiendo los mapamundis de Debenham y Maure; de donde no es difícil extrapolar, en nuestra propia estructura de simetría dimensional, el siguiente punto teórico en esa secuencia de vértices, que correspondería precisamente a los 5º𝜑N – 160º𝛌W, en el centro del Océano Pacífico; y, 3) la secuencia de vértices de Cabo de Hornos a Cabo de Agujas y Mar de Timor, corresponden a una loxodrómica, lo cual pone en evidencia su distribución armónica. Ello, sin duda, sobrepasa el hecho fortuito de la coincidencia casual; dicha regularidad debe, por tanto, responder a alguna ley espacial de simetria, cuya causalidad hipotetizaremos en otro lugar.
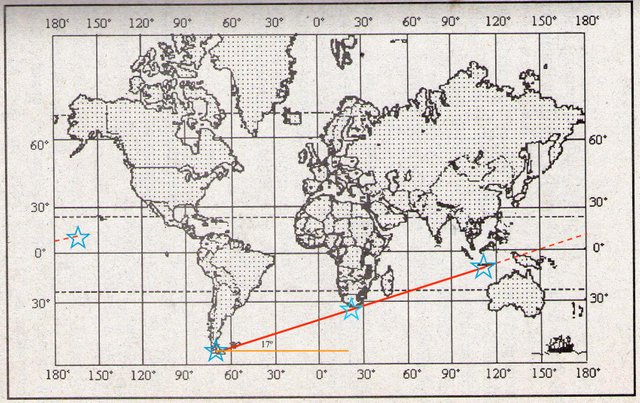;%20V%C3%A9rtices%20de%20Esfr%C3%A1gidas.jpeg)
Cuando observamos ese hecho, pasó a un segundo plano el análisis de la posición de las esfrágidas de la penínsulas de Arabia e India, fuera de esa secuencia, por lo que deben responder a una regularidad secundaria o derivada de la antes expuesta. En todo caso, estudiaremos ambos casos en un siguiente artículo más extenso en particular sobre este punto.