SLC21 Week4 - Recursion
Task 1.
Describe recursion as you understand it. Have you encountered recursion before? How is the word "fractal" related to recursion?
In programming, sometimes complex problems can be divided into simpler sub-problems of the same type. The technique used to solve these problems is called recursion. A recursive function is one that repeatedly calls itself to solve the sub-problems until the base case is met. Without a base case, the function will be stuck in an infinite loop.
What is a base case? A recursive function has two important parts: base-case and general/recursive case.
The base-case is the simplest version of the problem or a condition at which the recursion stops. This case doesn't need recursion to compute an answer.
On the other hand, the recursive/general case is one where the function calls itself repeatedly to solve smaller problems and gradually moves towards the base case.
Therefore, as a rule of thumb, recursive function must:
- have a base case
- call itself recursively
- change its state and move towards base case
Having a Computer Science background, I'm already familiar with the concept. It was a quite intimidating concept when I first learned about it, but once one gets the hang of it, the temptation to use it anywhere possible is huge because it beautifully simplifies complex problems.
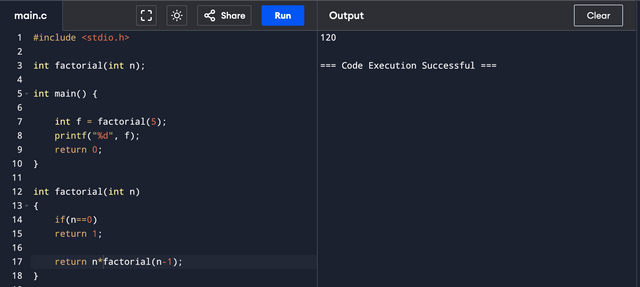
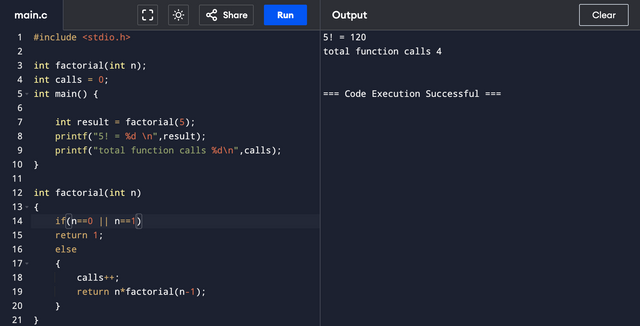
Let's look at the code to find factorial,
Base Case: n==0
That means the simplest or smallest instance of finding a factorial is 0. But I have also added n==1 later in this post as it will save us one recursive call and the result would still be right.
Recursive Case: n*factorial(n-1)
That means if we have to find the factorial of 5, then we need to compute 5x(4!), to compute 4!, we need to compute 4x(3!) and so on... The sub-problems will look like this...
5 * (4!)
5 * (4 * (3!))
5 * (4 * (3 * (2!)))
5 * (4 * (3 * (2* (1!))))
5 * (4 * ( 3 * ( 2 * (1 * (0!))))) [Base Case]
When the function is called recursively, a new stack frame of sub-problems is created until it hits the base case. Once the base case is reached, recursion stops and the unwinding phase begins, which means the function returns/computes the result by calling back up the stack of sub-problems, which are now easier to solve, like in the last line.
5 * (4 * ( 3 * ( 2 * (1 * 1))))
5 * (4 * ( 3 * ( 2 * 1)))
5 * (4 * ( 3 * 2))
5 * (4 * 6)
5 * 24
120
Fractals are geometric shapes that have similar patterns and are repeated numerously at different sizes. They are created by repeating the same procedures or equations.
Here the keywords are: repetition, same procedures, different sizes. Sounds familiar? Yes, this is like recursion. A good example is Serpinski's triangle, which is a fractal geometric figure constructed by dividing an equilateral triangle into numerous smaller equilateral triangles.
Task 2.
Explore the limit of what is the largest value of the factorial that can be calculated with a certain type of data.
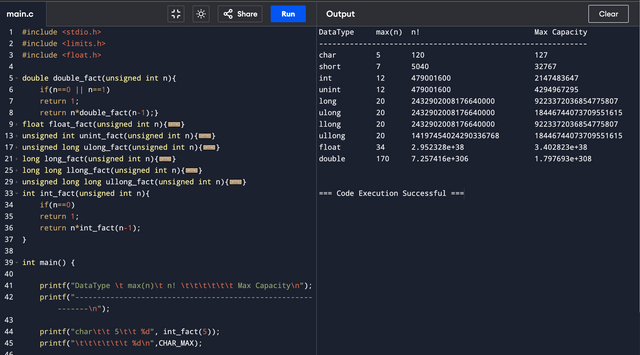
Initially, I wrote a single factorial function of integer return type. I type-cast the facotrial result to other data types but it gave wrong answers when the results got bigger. Therefore, I wrote multiple factorial functions with different return types to check the largest result that can be stored in different data types. Since factorials quickly jump to big numbers, it's better to thoughtfully choose the return type. If you notice, I have further refined my code for factorial.
I have not shown all the functions because it's almost same, just a few tweaks for different data types. If needed, I will share the rest but the above will give you an idea of what I did.
It's ridiculous to think that 13! can't be stored in integer, a doubleis though for real numbers but it can compute and store the correct answer of 170! as shown in the code.
For my understanding, I also displayed the maximum limits of each data type for comparison and then computed the facotrials of the largest numbers which can be correctly stored in the data type.
We have already learned the concept of overflow in data types in one of the previous lessons and further proved it in homework. That's why I haven't explained it again here.
Task 3.
Investigate how many calls the function will make before terminating. More details about this task are described in the lecture.
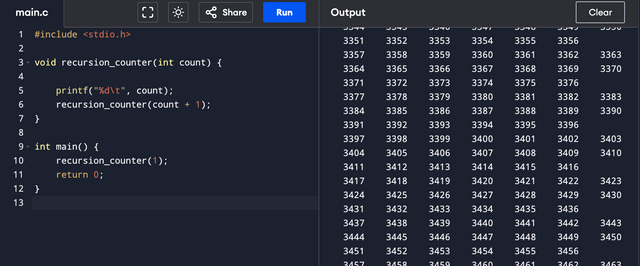
During recursion, each call to the function is stored in the call stack. When a function calls itself, a new stack frame is created that holds the local variables and execution details. Once the base case is reached, the stack unwinds and returns all the calls in reverse order.
Sometimes, when the recursion is too deep, it crosses the stack limit, resulting in stack overflow error. The stack limit depends on the system when working in the local environment. Since I'm using an online compiler for this course, a small limit is already set, so I wrote a simple code to check how many recursive calls it can make before it terminates with an error.
I got a different number every time I ran the code probably due to system load or other such reason. If I were using the local environment to write this code, I could have more control over this, I could do two things to increase or decrease the numbers of calls.
- Change the stack size through CLI
- Write tail-recursive functions
- Optimize the base case
A tail recursive function is one in which there's no further computation after the recursive call. In some compilers, such a function reuses the current stack frame for each call, thus taking less space and allowing more calls.
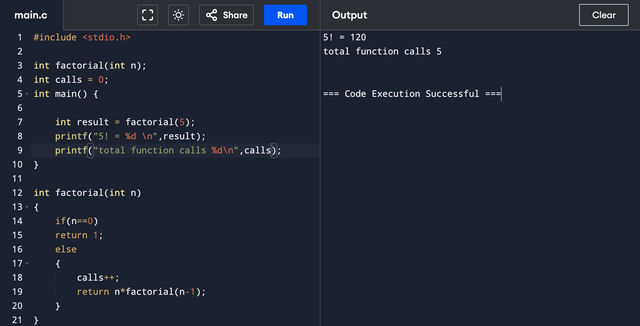
Since we are talking about facorials here, I optimized the base case of factorial function by adding the condition of n==1. It will reduce one rescusive call.
Previously, the recursive calls for n! were n. With new base case, the recursive calls are n-1
Task 4.
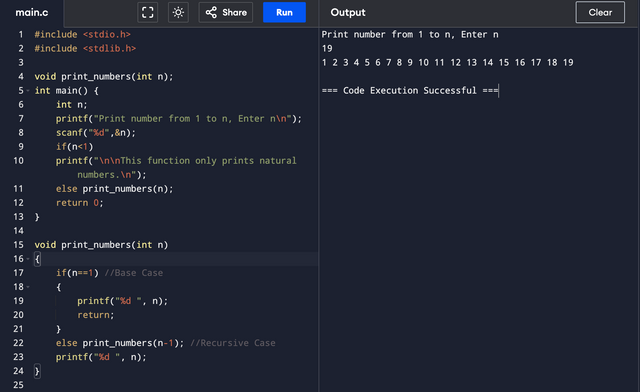
Print numbers from 1 to n.
The base case or smallest instance of this problem is when n=1. So, this will be the terminating condition for our recursive function. If n>1 then, we should simply increment each number by 1 until n and print all numbers, or we could decrement n until it reaches 1 and then print 1 to n. In my code, when the function calls itself, it doesn't print the result at once; instead, it stacks up all the calls until base case is reached and then prints the result in reverse order (which is actually the right order in this case.)
print_numbers(5)
print_numbers(4)
print_numbers(3)
print_numbers(2)
print_numbers(1) ---> Base Case
When the base case is achieved, the function jumps to line 23, which is a print command for n. It will start printing all the values of n that were stacked up.
prints 1
prints 2
prints 3
prints 4
prints 5
Remember, what goes first in the stack comes out last.
Task 5.
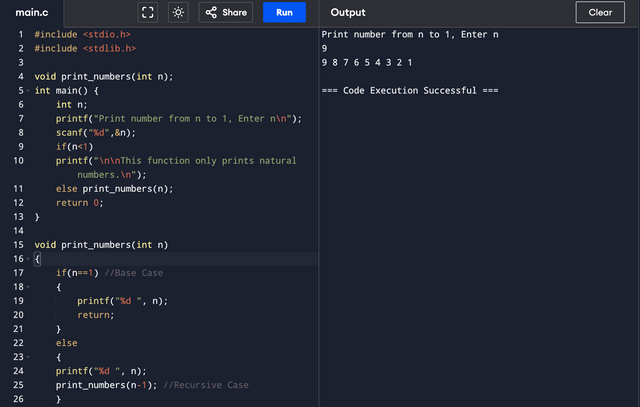
Print numbers from n to 1.
To print numbers from n to 1, I just moved the command of printing n before the recursive call. Doing so will print the current value of n before going into the recursive call as input. Since n will go first, the function will print it first, then n-1, (n-1)-1,.... 1. This way we can print the numbers in reverse order.
prints 5
print_numbers(5)
prints 4
print_numbers(4)
prints 3
print_numbers(3)
prints 2
print_numbers(2)
prints 1 ---> Base Case
Terminates.
Task 6.
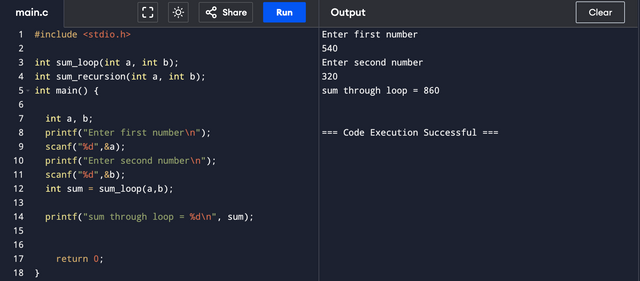
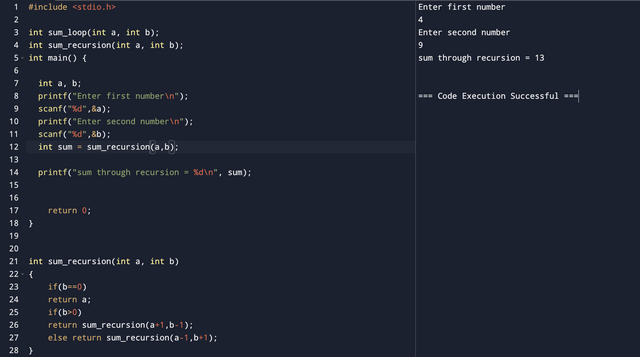
Write a function to calculate the sum of two numbers a+b. Do not use the a+b calculation directly.
Here I have taken user input and fed it to the sum_loop() which takes two numbers as input and performs addition using a loop without directly using the a+b command.
The loop increments the value of the first number by 1, repeats it the number of times the value of the second number, which means if a=5 and b=3 then it will add 1 to 5, 3 times. The loop also works for addition of negative numbers. It does so by decreasing a by 1, abs(b) times, which means if a=-5 and b=-3 then it will decrease -5 by 1, 3 times.
If we solve this problem through recursion... the base case will be when b=0 then it will return the other number and terminate. Otherwise, the function will call itself by increasing a by 1 and decreasing b by 1 until b is zero. Let's see an example.
sum_recursion(5,4);
sum_recursion(6,3)
sum_recursion(7,2)
sum_recursion(8,1)
sum_recursion(9,0) ---> base case
return 9
And if b is negative, then we will just do the opposite: decrease a by 1 and increase b by 1.
sum_recursion(5,-6);
sum_recursion(4,-5)
sum_recursion(3,-4)
sum_recursion(2,-3)
sum_recursion(1,-2)
sum_recursion(0,-1)
sum_recursion(-1,0) ----> Base Case
return -1
Task 7
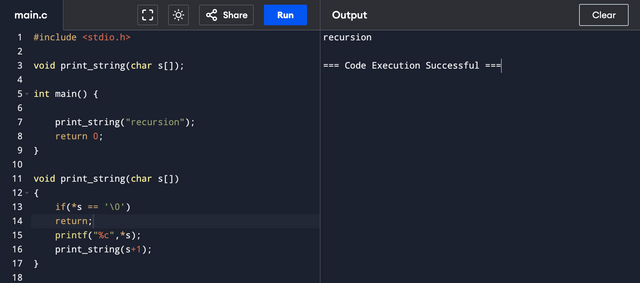
Print a string character by character (as an array).
As already explained in the question statement, if we have an array of characters s[] then s will have address of the array. s[0] will have first element of the array and *s will dereference the pointer and give value placed at address s.
Keeping this in mind, I wrote the code for printing the array character by character. The base case will be, of course, '\0' at which the program will terminate. I have simply printed each character by jumping to the address of the next element. The function calls itself with the address of the next element using s+1. I have added 1 because characters take only 1 byte.
"recursion"
Let's say the address of the array is 0000.
display r - using *s which points to0000
print_string(0000+1)
display e - using new adrress 0001
print_string(0001+1)
display c using new address 0002
print_string(0002+1)
display u using new address 0003
print_string(0003+1)
.
.
.
.
until the current address contains '\0'.
Task 8
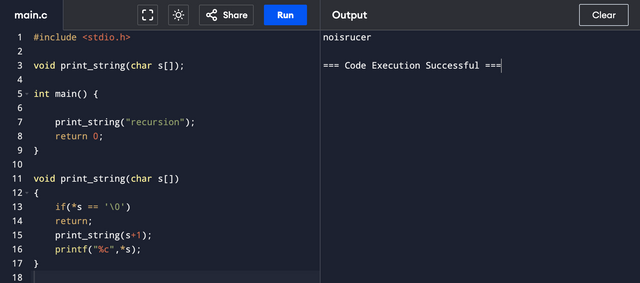
Similar to the previous task - but the line must be displayed backwards, turned around.
Here I made a small change to the previous code. Moved print command after the recursive call.
If the address is 0000.
print_string(0000)
print_string(0001)
print_string(0002)
print_string(0003)
.
.
.
.
Until the adddress contains '\0'
These calls stack up and after the base case, the program starts printing all characters stored in their respective addresses one by one in the reverse order. Because again, what goes first in the stack, comes out last.
display n
display o
display i
display s
.
.
.
display r