SLC21 Week4 - Recursia
Assalamualaikum my fellows I hope you will be fine by the grace of Allah. Today I am going to participate in the steemit learning challenge season 21 week 4 by @sergeyk under the umbrella of steemit team. It is about recursia. Let us start exploring this week's teaching course.
.png)
Understanding Recursion
Recursion is the process of defining a set of elements by operating on preceding elements using a formula or rule.
Recursion is a technique in computer science and mathematics. In recursion a problem is solved by breaking it down into smaller parts of the problem. In the recursion the function calls itself either directly or indirectly. The function solves progressively simpler versions of the problem until a base case is reached. When the base case is reached the recursion stops.
A base case is necessary in recursion. It provides a condition under which the function stops calling itself. Without this the function would call itself indefinitely. It will lead to an error like stack overflow.
How Recursion Works
- Recursive Step: The function calls itself to solve a simpler or smaller part of the same problem.
- Base Case: This is the stopping condition in recursion. It is usually the simplest form of the problem like
n = 0for factorials.
A classic example of recursion is calculating the factorial of a number n. The factorial function is defined as:
n! = n * (n-1)!and the recursion stops whenn = 0because0! = 1.
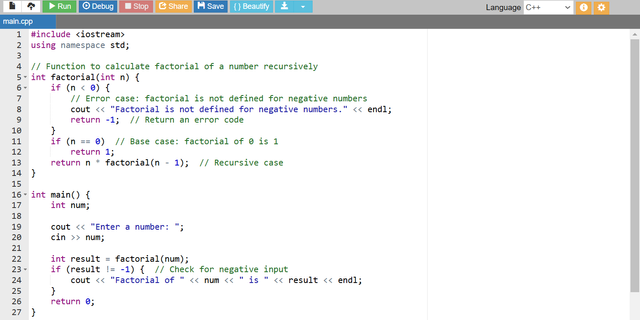
In this example the function factorial calls itself until it hits n = 0 at which point it stops and starts returning values back through the recursion chain.
I have encountered recursion while calculating the factorial of the number. In this the factorial calculation function calls itself again and again until it reaches to the base case. In the above program I have given the example of the factorial calculating program and the recursive function is in use in that program.
It’s often a natural way to think about problems where you have a complex structure that can be broken down into similar smaller subproblems.
Relationship Between "Fractal" and Recursion
A fractal is a geometric shape that can be split into parts. In this geometric shape each part is a reduced scale copy of the whole shape. In other words fractals show self similarity at different scales.
The relationship between recursion and fractals lies in the idea of repeating patterns and self similarity. The reality is that many fractals are generated using recursive algorithms. Here are some reasons:
Self Similarity: A fractal is often a pattern that repeats itself. It repeats at different levels of magnification. This shows how recursive functions work by breaking down a problem into smaller and similar subproblems.
Recursive Generation of Fractals: Fractals can be created through recursive algorithms. Because in the recusrive algorithms each iteration of the function draws a smaller version of the pattern. And then it repeats the process. For example:
- The Sierpinski Triangle can be created recursively by starting with an equilateral triangle and recursively cutting out smaller triangles from it.
- The Mandelbrot Set one of the most famous fractals also involves repeatedly applying a mathematical function to generate a complex and self similar structure.
Example of a Recursive Fractal (Sierpinski Triangle)
The Sierpinski triangle is a simple fractal that can be generated using recursion. Here is the idea:
- Start with a triangle.
- Divide it into three smaller triangles.
- Recursively apply the same process to each of these smaller triangles.
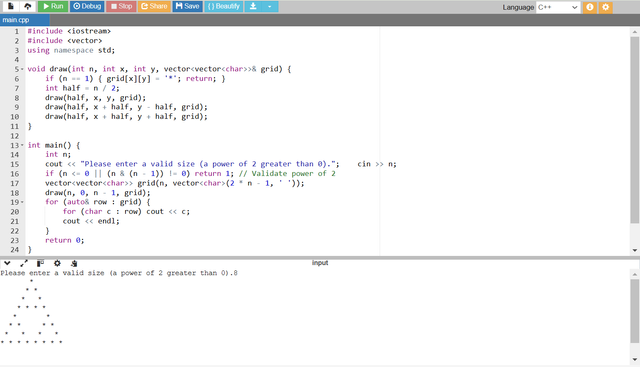
This C++ program generates a Sierpinski Triangle by recursively subdividing a triangle into smaller ones. The main logic is encapsulated in the draw function. It takes the size of the current triangle (n) and its top vertex's coordinates (x, y) as well as the 2D grid (grid) to store the pattern. The base case places a star (*) when n equals 1 while the recursive case divides the current triangle into three smaller ones. The program starts by checking if the input size n is a positive power of 2. Then it initializes a 2D grid large enough to accommodate the fractal. The draw function is called to fill the grid with stars and the resulting pattern is displayed row by row. The program ensures efficiency and clarity by keeping the grid size optimal and simplifying the recursive logic.
Here is the table to highlight the relationship betwen the fractal and recursion.
| Concept | Description | Relationship |
|---|---|---|
| Recursion | A technique where a function calls itself to solve smaller instances of the same problem, stopping at a base case. | Recursion breaks down a problem into smaller subproblems, similar to how fractals repeat smaller patterns. |
| Fractals | Patterns that repeat themselves on different scales, exhibiting self-similarity. | Many fractals are generated using recursive algorithms due to their self-repeating, smaller structures. |
| Connection | Recursion and fractals are connected through the idea of repeating structures or patterns. | Fractals use recursion to generate self-similar patterns at different scales. |
Explore the limit of what is the largest value of the factorial that can be calculated with a certain type of data.
The largest factorial that can be calculated with a certain data type depends on the size or the maximum value the data type can hold. Different data types in programming languages like C or C++ have different limits for how large a number they can store.
For example a char in C typically holds values in the range -128 to 127 if signed or 0 to 255 if unsigned. This range is too small to store even relatively small factorials. On the other hand the larger data types like int, long and long long can hold much larger values.
Now to explain this in depth let us cosnider common data types and their limits. And we will see the largest factorial (n!) that we can calculate without overflow.
Key Data Types and Their Limits
- char: It is typically 1 byte and the range of values is
-128 to 127(signed) or0 to 255(unsigned). - short: It is typically 2 bytes and the range of values is
-32,768 to 32,767(signed) or0 to 65,535(unsigned). - int: It is typically 4 bytes and the range of values is
-2,147,483,648 to 2,147,483,647(signed). - long: It is typically 4 or 8 bytes and depending on the system the range of values is usually
-2,147,483,648 to 2,147,483,647(signed) for 4 bytes or much larger for 8 bytes. - long long: It is typically 8 bytes and the range of values is
-9,223,372,036,854,775,808 to 9,223,372,036,854,775,807(signed). - unsigned types: These types only store positive values and have higher upper limits.
Largest factorial (n!) that fits within the limits of each data type
Here I will calculate the largest factorialn! that fits into each data type until we exceed the upper limit of the data type.
Table of Largest Factorial for Different Data Types
| Data Type | Max Value | Largest n (such that n! fits) | n! |
|---|---|---|---|
char | 127 (signed) or 255 (unsigned) | 5 | 120 |
short | 32,767 (signed) or 65,535 (unsigned) | 7 | 5,040 |
int | 2,147,483,647 (signed) | 12 | 479,001,600 |
long | 2,147,483,647 (signed) | 12 | 479,001,600 |
long long | 9,223,372,036,854,775,807 (signed) | 20 | 2,432,902,008,176,640,000 |
unsigned long long | 18,446,744,073,709,551,615 | 20 | 2,432,902,008,176,640,000 |
Explanation
For
char(8-bit): A signedcharcan hold values between -128 and 127. The factorial for values larger than 5 exceed the capacity of achar. Hence,5!is the largest factorial that fits in achar.For
short(16-bit): A signedshortcan hold values between -32,768 and 32,767. The factorial7! = 5040is the largest factorial that can fit in a signedshort.For
int(32-bit): A signedintcan hold values from -2,147,483,648 to 2,147,483,647. The largest factorial that fits in anintis12! = 479,001,600.For
long(typically 32-bit or 64-bit): Iflongis 32-bit (same asint), then12! = 479,001,600is the largest value. However, on systems wherelongis 64-bit, we could calculate much higher factorials, such as20!, which is well within the range of a 64-bitlong.For
long long(64-bit): A signedlong longcan store much larger values (up to9,223,372,036,854,775,807), so the largest factorial that fits in along longis20! = 2,432,902,008,176,640,000.For
unsigned long long: Since it doesn't need to account for negative numbers, anunsigned long longcan hold larger values. The largest factorial that fits is20!.
Factorial functions grow exponentially.
5! = 12010! = 3,628,80015! = 1,307,674,368,00020! = 2,432,902,008,176,640,000
As you can see, the factorial function increases very quickly and it soon exceeds the limits of many standard data types.
We can see that as the size of the data type increases the largest factorial that can be computed also increases. However even long long has limits. Because after a certain point very large factorials will require specialized data types such as arbitrary precision libraries to compute and store.
Investigate how many calls the function will make before terminating. more details about this task are described in the lecture.
It is interesting to investigate that how many call teh function will make before its termination. It is actually related to the depth of recursion. Now for the investigation first of all I will explain the recursion call stack.
Understanding the Recursion Call Stack
Each time a function calls itself in the recursion it adds a new entry to the call stack. It serves as a data structure to track the active function calls. The depth of recursion refers to how many function calls are stacked up before the base case is reached.
For example here is the recursive factorial function:
int factorial(int n) {
if (n == 0) // base case
return 1;
return n * factorial(n - 1); // recursive call
}
How Many Calls Will Be Made?
In the case of the factorial function when factorial(n) is called then the function makes a recursive call to factorial(n-1). And it keeps on calling the function until it reaches the base case (n == 0). The number of recursive calls made is equal to n. Beecause for each value of n a recursive call is made to n-1 until it reaches 0.
Example with factorial(5):
factorial(5)callsfactorial(4)factorial(4)callsfactorial(3)factorial(3)callsfactorial(2)factorial(2)callsfactorial(1)factorial(1)callsfactorial(0)factorial(0)is the base case and stops the recursion
In this case, 6 function calls are made before the recursion terminates. One call for each of 5, 4, 3, 2, 1, and 0.
General Case
For any call to factorial(n) the number of calls made will be equal to n + 1 as the recursive calls include the base case which is factorial(0). It means if we take n=10 then the number of recursive calls will 11 and similarly if n = 20 then the number of recursive calls will be equal to 21.
Factors Affecting Recursion Calls
Depth of Recursion: The deeper the recursion the more calls will be made. This depth depends directly on the input size. In the case of factorial the depth is simply the number
n.Base Case: Every recursive function must have a base case or termination condition. It ensures the recursion will stop after a certain number of calls. If the base case is never reached then the recursion will continue indefinitely and lead to stack overflow. So base case is necessary.
System Stack Limitations: Different systems have different limits for the depth of recursion they can handle. If the recursion depth exceeds the maximum allowed stack size then the program will crash with a stack overflow error. For example on some systems the default stack size might allow around 1000 recursive calls before running out of memory. On 32-bit systems the maximum call stack size is generally smaller as compared to 64-bit systems. Therefore a 64-bit machine can usually handle deeper recursion levels.
How Many Calls Before the Function Terminates?
To investigate how many recursive calls are made before termination we can run a test using a recursive function like the one for calculating factorial. The number of calls will depend on the value of n.
Here is a simple C++ program that tracks how many recursive calls are made before termination of the recursive function:
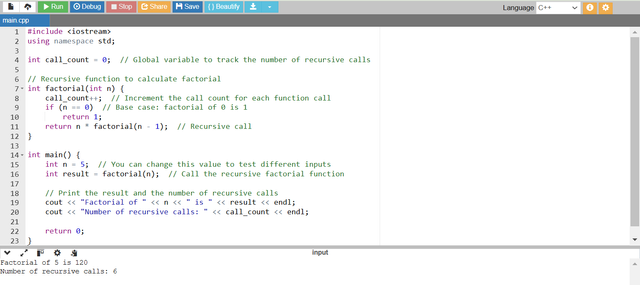
You can see that I have run the program by giving n = 5 and it has calculated the factorial of this number as 120. And it has calculated that the function made 6 recursive calls where 5 calls for the main function and 1 call for the base case. So we can now say that the number of calls for a recursive function main depends upon n+1.
The number of recursive calls will be the same as the value of
nplus one because of the base case call. This is demonstrated by the globalcall_countvariable in the code above.To investigate how many calls can be made before the program crashes due to stack overflow we are incrementing
nuntil the program fails. For example on a typical system we can be able to make several thousand recursive calls before running into a stack overflow.
If we summarize it in afew lines then:
- For a function like
factorial(n)the number of recursive calls is equal ton + 1since the base casefactorial(0)counts as one call. - The recursion depth is limited by the system's stack size. If the recursion exceeds this depth then a stack overflow issue will occur.
- Some systems provide ways to increase the stack size or optimize tail recursion to handle deeper recursive calls.
Print numbers from 1 to n
It is just a common program where we can easily print numbers from 1 to n. To print numbers from 1 to n in C++ we can use iteration and recursion method. Both approaches are given below:
Iterative Approach
Recursive Approach
1. Iterative Approach (Using a Loop)
The iterative approach is the most common way to print numbers from 1 to n. It uses a simple for loop. When we need to print numbers from 1 to n or in any range then mostly this method is used.
C++ Code (Iterative):
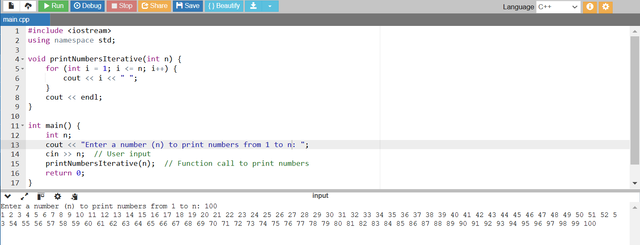
- In this iterative approach to print numbers from 1 to n I have used a
forloop to iterate through numbers from 1 ton. - Each number is printed on the same line but with the space.
- After the loop a newline character (
endl) is printed to move the cursor to the next line. - I have assigned n as 100 it means the program should print numbers atrting from 1 to 100 consecutively. And it perfomed the same as expected you can see it has printed numbers from 1 to n by using this iterative approach with the help of the
forloop.
2. Recursive Approach (Using Recursion)
This approach is also very useful but in this approach we do not use loop but we use a recursive function which calls itself again and again until the base case is reached. In this the function will call until it has printed number from 1 to n. In this logic the base case will 1.
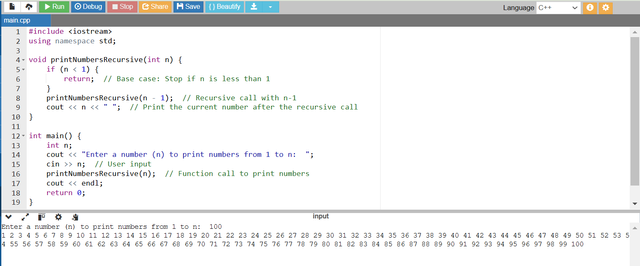
- In this recursive approach to print numbers from 1 to n. The recursive function
printNumbersRecursive(int n)calls itself withn - 1untilnbecomes 1. - The base case for recursion is
n < 1. This is the point at which the function terminates. - After the recursive call the current value of
nis printed. - This causes the numbers to be printed in increasing order as the printing happens after the recursion.
In the program you can see that I have given 100 as the value of n. The program has printed numbers from 1 to given bnumber n which is 100 by recursive function. The function has called itself again and again until it has reached to its base case.
How the Recursive Approach Works
If n = 5 then the recursive calls will happen like this:
printNumbersRecursive(5)will callprintNumbersRecursive(4)printNumbersRecursive(4)will callprintNumbersRecursive(3)printNumbersRecursive(3)will callprintNumbersRecursive(2)printNumbersRecursive(2)will callprintNumbersRecursive(1)printNumbersRecursive(1)will reach the base case and start returning.
When the base case is reached (n == 0) then the function starts returning back. And in this way it prints numbers in increasing order.
Both methods will achieve the same result and the choice between them depends on the specific use case.
Print numbers from n to 1
To print numbers from n to 1 in C++ we can also use both iteration with a loop and recursion. Below are the two approaches for printing numbers in reverse order from n to 1.
1. Iterative Approach (Using a Loop)
This approach uses a simple for loop to print numbers in reverse order starting from n and decrementing down to 1. This is similar to the previous task but here the order for printing the numbers is different. In the previous task we printed numbers from 1 to n but here by using the for loop we will print numbers from n to 1.
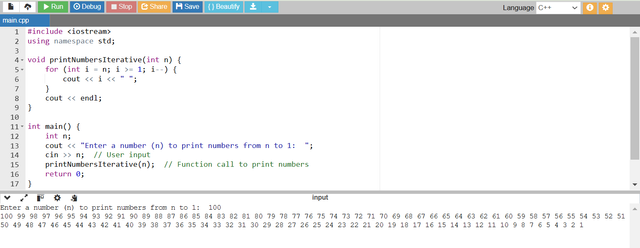
- In the above program I have used a
forloop. The loop is starting fromn. Andiis decrementing in each iteration byi--untilireaches 1. - Each number is printed on the same line but separated by a space.
- After the loop a newline character
endlis printed to move the cursor to the next line. - In this way the program is printing numbers from
nto1. - Here I have given
n = 100and the program has printed numbers from 100 to 1 and after each iteration the number n is decreasing until it reaches 1.
2. Recursive Approach (Using Recursion)
This approach has to print the same output but here we will use recursive algorithm to print the numbers from n to 1. In this we will use a recursive function and it will call itself with n-1 until it reaches the base case. And in this way it prints the numbers.
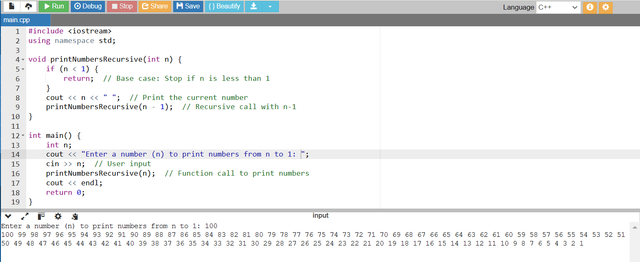
- The function
printNumbersRecursive(int n)printsnthen calls itself withn - 1untilnis less than 1. - The base case is when
n < 1and it terminates the recursion. - Numbers are printed as the recursion unwinds which results in printing them from
ndown to 1. - Here you can see that I have given n as 100 and the recursive function has printed the numbers from 100 to 1 by calling itself again and again.
How the Recursive Approach Works
If n = 5, the recursive calls will happen like this:
printNumbersRecursive(5)prints5, then callsprintNumbersRecursive(4)printNumbersRecursive(4)prints4, then callsprintNumbersRecursive(3)printNumbersRecursive(3)prints3, then callsprintNumbersRecursive(2)printNumbersRecursive(2)prints2, then callsprintNumbersRecursive(1)printNumbersRecursive(1)prints1, then callsprintNumbersRecursive(0)printNumbersRecursive(0)reaches the base case and terminates the recursion.
Numbers are printed in the order 5 4 3 2 1 as the recursive function unwinds.
Here is a comparison table to show the difference between Iterative and Recursive approaches:
| Aspect | Iterative Approach | Recursive Approach |
|---|---|---|
| Simplicity | Simpler and easier to understand for straightforward tasks. | More elegant but can be complex for simple tasks. |
| Efficiency | Generally faster and uses less memory (no extra stack space). | Can be less efficient due to overhead of recursive calls and stack space usage. |
| Use Case | Ideal for tasks that can be solved with simple loops (e.g., printing numbers). | Best for problems that have a natural recursive structure (e.g., fractals, tree traversal). |
| Memory Usage | Uses constant memory, as it only requires a loop variable. | May consume more memory due to the function call stack. |
| Elegance | More direct but less elegant for complex, recursive problems. | More elegant for problems involving repeating subproblems. |
Write a function to calculate the sum of two numbers a+b. Do not use the a+b calculation directly. First perform this task using a loop (1 point), maybe it will tell you how to use recursion here and perform this task
It is looking interesting to calculate the sum of two numbers without the classic calculation where we directly add two numbers. But here we need to find out the sum without directky adding two numbers. So to calculate teh sum first of all I will use iterative approach with the help of loop. After that I will perform the same functionality but with the help of recursion.
In both approaches, the key concept is that we will simulate the addition of a and b without directly using the + operator by either repeating the addition in a loop or through recursive function calls. This illustrates a way to handle basic arithmetic operations indirectly by breaking them down into smaller and more manageable tasks.
1. Using a Loop (Iterative Approach)
- We will start with
aas the initial value. - Then we will run a loop
btimes by incrementingaby 1 on each iteration. - After the loop ends the value of
awill have increased bybwhich is the sum ofa + b.
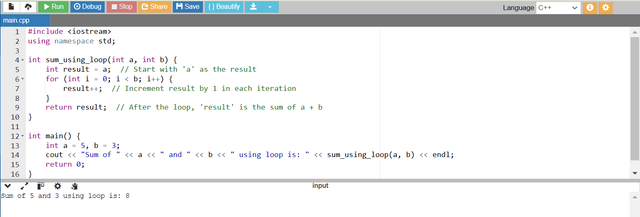
- The
sum_using_loopfunction initializes theresultvariable with the value ofa. - It then runs a
forloopbtimes by incrementing theresultby1in each iteration. - Once the loop finishes then the final value of
resultis returned which is the sum ofaandb.
Example:
- For
a = 5andb = 3the loop will execute 3 times while incrementingresultto8. - The result is
8which is the sum of5 + 3.
So in this way we can find the sum of the two numbers without directly adding them but using loop.
2. Using Recursion (Recursive Approach)
- In the recursive approach the function will call itself by decreasing
bby 1 each time. But on the other hand it will incrementaby 1. - This will continue until
bbecomes 0. And whenbbecomes 0 the recursion stops andacontains the sum.
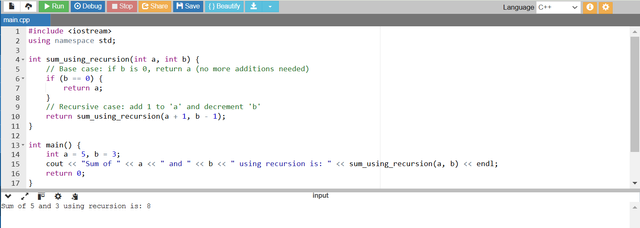
- The
sum_using_recursionfunction first checks ifb == 0. If it is then it means the base case is reached and it simply returnsaas adding 0 toagivesaitself. - If
bis not 0 the function calls itself witha + 1andb - 1effectively adding 1 toaand reducingbby 1. - This process continues until
bbecomes 0 and then the final value ofais returned.
Example:
- For
a = 5andb = 3the recursive function works as follows:- First call:
sum_using_recursion(5 + 1, 3 - 1) -> sum_using_recursion(6, 2) - Second call:
sum_using_recursion(6 + 1, 2 - 1) -> sum_using_recursion(7, 1) - Third call:
sum_using_recursion(7 + 1, 1 - 1) -> sum_using_recursion(8, 0) - Base case reached:
sum_using_recursion(8, 0)returns8.
- First call:
- The result is
8which is the sum of5 + 3.
After walking through these botrh techniques we can conclude:
Loop Method (Iterative): This method uses a
forloop to increment the value ofaby1forbtimes. It is an iterative approach that simulates the addition process by repeating an action or incrementinga.Recursion Method (Recursive): This method uses recursion to reduce the problem. Each recursive call adds 1 to
aand reducesbby 1 untilbreaches 0. And at this point the sum is returned.
Both methods avoid using the + operator directly and instead rely on iterative or recursive processes to simulate the addition of two numbers.
Print a string character by character
This question involves the understanding of how to manipulate strings in C++ by using both array indexing and pointer arithmetic. In C++ the strings are essentially arrays of characters with the last character being a null terminator ('\0') to mark the end of the string.
Now according to the question we need to print each character of a string one by one using two different approaches. The first approach is to print the string character by character by accessing characters through array indexing such as s[i] and the second method is to use pointer arithmetic such as*p where p is a pointer to the string.
In the first method we loop through the string using an index and print each character until the null terminator is encountered.
In the second method we use a pointer to iterate through the string by dereferencing the pointer to access each character and advancing the pointer with
p++.
Both methods achieve the same outcome while printing the string character by character but by using different techniques in C++ for accessing and manipulating array data.
Using Array Indexing

- This method uses array indexing to access and print each character of the string.
- The array
s[]is automatically treated as a pointer to the first character of the string and we can access each element by its index (s[i]). - A
forloop is used to iterate over the array. The loop continues as long ass[i] != '\0'. It means it keeps iterating until it reaches the null terminator'\0'which marks the end of the string. - We start with
i = 0and each iteration printss[i]followed by a space. After each iterationiis incremented by 1. - The loop terminates when
s[i]is equal to'\0'.
As our input string is recursia so the program has printed this string character by character in r e c u r s i a.
Using Pointer Arithmetic
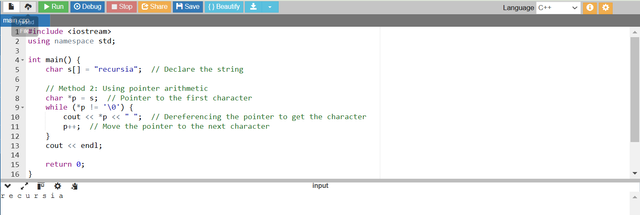
This method uses pointer arithmetic to access and print each character of the string.
We define a pointer
pthat points to the first character of the string likep = s.A
whileloop is used to iterate through the string. The loop continues as long as the dereferenced pointer*pis not the null terminator'\0'.*pdereferences the pointer to get the character at the current pointer location.After printing
*pthe pointerpis incremented usingp++and by moving it to the next character in the string.The loop stops when the pointer points to the null terminator
'\0'.As our input string is recursia so the program has printed this string character by character in
r e c u r s i a.
Summary of Key Differences Between the Two Methods
| Aspect | Method 1: Array Indexing | Method 2: Pointer Arithmetic |
|---|---|---|
| Accessing Characters | Uses the index i to access s[i]. | Uses a pointer p and dereferences it (*p). |
| Iteration Mechanism | Uses a for loop that runs until s[i] != '\0'. | Uses a while loop that runs until *p != '\0'. |
| Pointer Involvement | No pointer manipulation, just array indexing. | Uses a pointer (p) and moves it with p++. |
| Character Access | Accesses characters via s[i]. | Accesses characters via *p. |
- Array Indexing is a straightforward way to traverse and print the string by directly accessing each element using an index.
- Pointer Arithmetic demonstrates the flexibility of pointers in C++ by moving through the string with pointer arithmetic and dereferencing to access characters.
Both methods ultimately achieve the same result of printing the characters of the string "recursia" but they demonstrate two different ways of interacting with the string one via indexing and the other using pointer manipulation.
Similar to the previous task - but the line must be displayed backwards, turned around.
To solve the problem of printing a string backwards in C++ we can use both array indexing and pointer arithmetic methods. This is similar to the previous task but with the goal of reversing the order of characters before printing.
We can use the same two approahes here:
- Array Indexing: We can loop through the string from the last character to the first by printing each character one by one.
- Pointer Arithmetic: We can use a pointer to point to the last character of the string and then move the pointer backwards by printing each character until we reach the first one.
Using Array Indexing (Backward)
This method involves using the length of the string to print characters starting from the last one and iterating backwards.
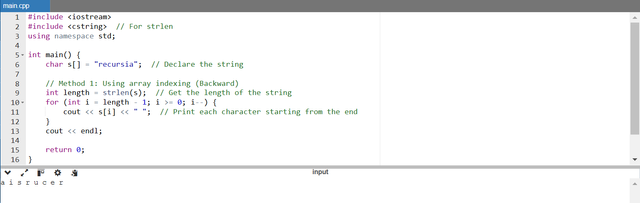
- First we calculate the length of the string by using
strlen(s)which returns the number of characters before the null terminator. - We start from the last character (
s[length - 1]) and move backwards to the first character (s[0]) by using aforloop. - The loop prints each character followed by a space and the loop terminates when
ibecomes less than 0.
As our input string is recursia so the program has printed this string character by character in the reverse order in a i s r u c e r.
Using Pointer Arithmetic (Backward)
This method involves using a pointer that points to the last character and moves backwards through the string.
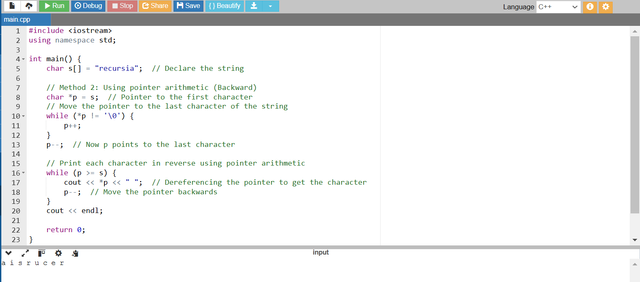
- We initialize a pointer
pto point to the first character of the string (s). - First we move the pointer
pto the last character of the string by incrementing it until we reach the null terminator ('\0'). - Once
ppoints to the null terminator we decrement the pointer (p--) to move to the last character of the string. - Then we use a
whileloop to print each character by dereferencing the pointer (*p) and we move the pointer backwards untilpreaches the beginning of the string (p >= s).
As our input string is recursia so the program has printed this string character by character in the reverse order in a i s r u c e r.
Summary of Key Concepts for Reversing a String
| Aspect | Method 1: Array Indexing (Backward) | Method 2: Pointer Arithmetic (Backward) |
|---|---|---|
| Accessing Characters | Uses the index i to access s[i] from the end. | Uses a pointer p and moves it backwards (p--). |
| Iteration Mechanism | Loops from length - 1 down to 0. | Moves pointer from the null terminator to the start. |
| Pointer Involvement | No pointer manipulation. | Uses pointer manipulation to move through the string in reverse. |
| Character Access | Accesses characters via s[i]. | Accesses characters via *p. |
To print a string backwards in C++ we can either use array indexing by iterating from the end to the beginning of the string or we can use pointer arithmetic by moving a pointer from the null terminator towards the start of the string. Both methods involve reversing the order in which we access and print the characters.
I invite @suboohi, @irawandedy, and @chant to learn strings.
I have compiled all the code of the tasks in a famous online compiler which is OnlineGDB