SLC21 Week1 - Learn more about variable types. Subroutines. Practice problems.
 |
|---|
Come up with your own example similar to float f=7/2; that illustrates the loss (distortion) of value during division. Show how to fix it. Explain why this happens and how you fixed it
Here I have a similar to my own that illustrates the loss (distortion) of value during division: let's take a look at it as shared below 👇.
int a = 5;
int b = 2;
float result = a / b;
From the given example above, the result is expected to be 2.5, and the actual value that is assigned to the result will be 2.0.
Reason
The reason why it happens is that in C++, when both operands in a division are integers like for example,
5and2the operation performs integer division, throwing away the remainder and resulting in an integer (5/2becomes2).Also, the result of the integer will then be converted to a float and stored in
resultwhich the precision is lost already.
Fixing the Distortion
For me, to avoid this loss of precision, I can make at least one of the operations a double or float to force floating point division rather than integer division.
int a = 5;
int b = 2;
float result = (float)a / b;
I can also directly define a or b as a floating point number as shown below 👇.
float a = 5.0;
int b = 2;
float result = a / b;
Doing that above, the result will perfectly (correctly) hold the value 2.5.
Choose a data type independently and illustrate the limitations of its range: demonstrate the lower boundary (crossing the minimum value) and the upper boundary (crossing the maximum value). Also, demonstrate crossing the boundary during multiplication, explaining the results.
Now, let me consider using the int data in C++. Normally, int is a 32-bit signed integer with a range that begins from -2,147,483,648 to 2,147,483,647 in most systems.
Lower and Upper Boundaries Illustration;
Let's say that in a situation where we try to exceed the maximum value of an int, overflow is what we will get.
#include <iostream>
using namespace std;
int main() {
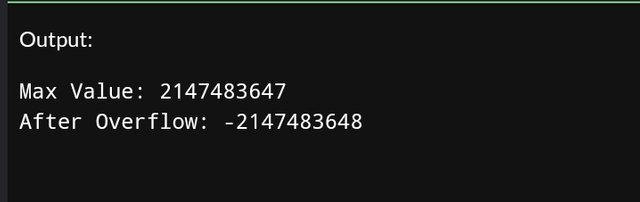
int maxValue = 2147483647; // Maximum value for 32-bit int
cout << "Max Value: " << maxValue << endl;
maxValue += 1; // Cross the upper boundary
cout << "After Overflow: " << maxValue << endl;
return 0;
}
Interpretation:
- Adding
1to2147483647causes an overflow, wrapping the value around to the minimum possible integer as-2147483648.
Lower Boundary
Also, if we should go below the minimum value, underflow is what we will get.
#include <iostream>
using namespace std;
int main() {
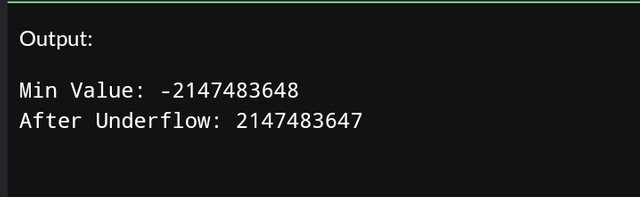
int minValue = -2147483648; // Minimum value for 32-bit int
cout << "Min Value: " << minValue << endl;
minValue -= 1; // Cross the lower boundary
cout << "After Underflow: " << minValue << endl;
return 0;
}
Interpretation:
- Substracting (minusing)
1from2147483648wraps around to the maximum integer,2147483647.
Crossing Boundaries during Multiplication:
Here, we are going to demonstrate overflow during multiplication which we have shared below 👇.
#include <iostream>
using namespace std;
int main() {
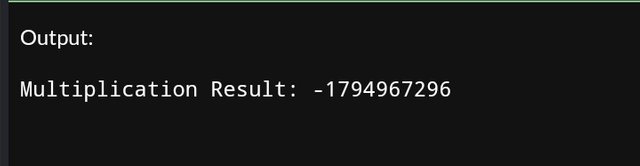
int a = 50000;
int b = 50000;
int result = a * b; // Attempting to multiply beyond the range
cout << "Multiplication Result: " << result << endl;
return 0;
}
Interpretation;
50000 * 50000should give us2500000000, which has exceeded the maximum range for anint. The result we got is an overflow leading to an unexpected negative value.-1794967296.
Using a Large Data Type
For us to handle larger values and prevent (stop) overflow, we will have to use a 64-bit integer, long long which the code for it is shared below 👇.
#include <iostream>
using namespace std;
int main() {
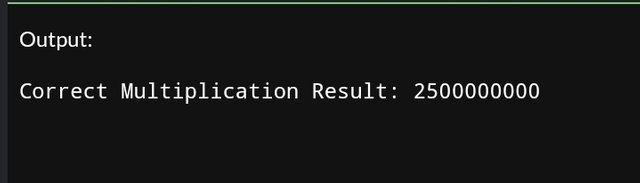
long long a = 50000;
long long b = 50000;
long long result = a * b; // Now within range
cout << "Correct Multiplication Result: " << result << endl;
return 0;
}
Find your example of 0.1!=0.1, meaning there is a certain value in a variable, but the check shows a different number. Or 0.1+0.2!=0.3. Why is this happening?
The limitations of floating point arithmetic in computers are what make this behavior happen. Below 👇 is an example illustrating 0.1 + 0.2! = 0.3:
#include <iostream>
using namespace std;
int main() {
float a = 0.1;
float b = 0.2;
float result = a + b;
cout << "0.1 + 0.2 = " << result << endl;
if (result == 0.3) {
cout << "Equal to 0.3" << endl;
} else {
cout << "Not equal to 0.3" << endl;
}
return 0;
}
Why This Happens
Floating point numbers like 0.1 and 0.2 cannot be represented in binary exactly. Instead, they are stored as approximations which leads to small errors in calculation. Having said that, when if 0.1 and 0.2 are added, their binary representations combine into a value that is close to 0.3, but not exactly 0.3. The equality check fails as a result.
Solution
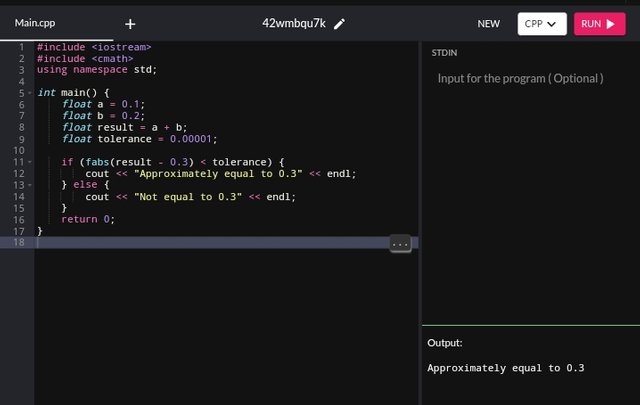
For a perfect solution tolerance needs to be used to compare floating point numbers correctly we will have to check if they are close enough by defining a small tolerance value:
#include <iostream>
#include <cmath>
using namespace std;
int main() {
float a = 0.1;
float b = 0.2;
float result = a + b;
float tolerance = 0.00001;
if (fabs(result - 0.3) < tolerance) {
cout << "Approximately equal to 0.3" << endl;
} else {
cout << "Not equal to 0.3" << endl;
}
return 0;
}
With the solution of tolerance, we can be able to also check if the difference between result and 0.3 is smaller than a tiny threshold, treating them as equal (=). This approach helps us to avoid problems caused by floating point precision limitations.
Based on the example of counting digits in a number, write a program that determines: (one of your choice): the sum of the digits of a number, (3456 => 3+4+5+6=18), sum(3456) = 18 the sum of the digits of a number, but finding it for the sum, and for the sum of the sum, until you get a one-digit sum - (3456 => 3+4+5+6=18 => 1+8=9). Here you can do it directly as stated in the task, it won't be the best option, but you can think and find a more efficient solution, which I always ask to find. sum1(3456)=9 find the number of a specified digit in a number count_d(143112, 1) = 3, count_d(143112, 5) = 0.
Here I have created a program that finds the digital root of a number, where we keep summing (adding) the digits of a number until we get a single-digit result. For example, using 3456, the program will help us to sum its digit as shared below 👇.
- ( 3 + 4 + 5 + 6 = 18 )
- Since 18 is still a two-digit number, we repeat with ( 1 + 8 = 9 ).
So, the digital root of 3456 is 9.
We can use these two approaches; straightforward or modular arithmetic approach. Let's try the first approach and see what we can get.
Approach 1
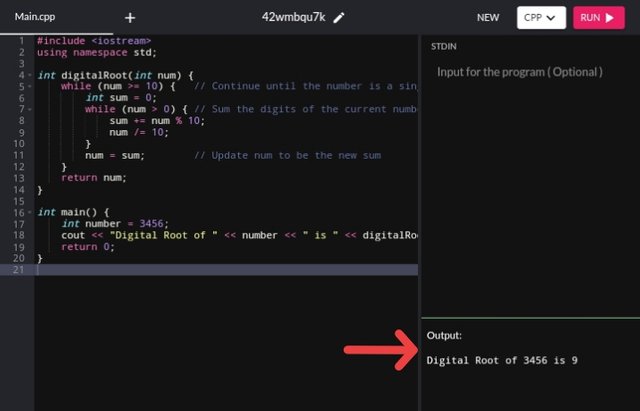
I do call this approach, the iterative summing of digits. In this approach, we will continually sum the digits of the number until the sum is a single-digit value. Below 👇 is the code that we need for this approach.
#include <iostream>
using namespace std;
int digitalRoot(int num) {
while (num >= 10) { // Continue until the number is a single-digit
int sum = 0;
while (num > 0) { // Sum the digits of the current number
sum += num % 10;
num /= 10;
}
num = sum; // Update num to be the new sum
}
return num;
}
int main() {
int number = 3456;
cout << "Digital Root of " << number << " is " << digital root(number) << endl;
return 0;
}
Interpretation
The outer
whileloop continues as long as the number has more than one (1) digit.Inside the loop, is where I create a new SIM by adding (summing) each digit of the current number. This is simply done by taking the remainder
num % 10to get the last digit and then minimizing the number by dividing it by 10num/=10.After I finish summing all digits, I then set
numto this sum, and the process repeats itself untilnumbecomes a single digit.
Approach 2
Here will be using the modular arithmetic approach. There is a shirt way of doing this without repeating summing as shared 👇 below.
Digital Root = 1 + (num - 1) % 9
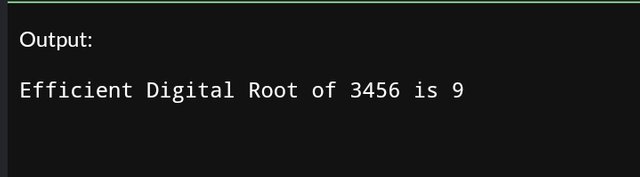
In the above formula, the digit root of a number is equivalent to the remainder when it is divided by 9, adjusted for zero. Below is the code for this approach.
#include <iostream>
using namespace std;
int digitalRootEfficient(int num) {
if (num == 0) return 0;
return 1 + (num - 1) % 9;
}
int main() {
int number = 3456;
cout << "Efficient Digital Root of " << number << " is " << digitalRootEfficient(number) << endl;
return 0;
}
Interpretation
- If
numis zero, its digit root is also zero. - If
numis not zero we can then use1 + (num - 1) % 9as the formula to directly calculate the digit root.
Congruence properties of numbers are the reason why the modular arithmetic approach works. It is an approach that reduces the repeated process of summing digits to a single computation.
Example Based on Output
For
3456both methods will have9.For
12345, the iterative method would have to go through the steps shared below 👇.1 + 2 + 3 + 4 + 5 = 15
1 + 5 = 6, giving a digital root of
6.The modular arithmetic approach directly calculates
1 + (12345 - 1) % 9 = 6.
The benefit of using the modular arithmetic approach is that it helps us avoid repeatedly summing digits and looping when we are summing large numbers. As for the straightforward method it provides us with a clearer understanding of the process behind finding a digital root.
As preparation for the next lesson and to review the past, find the largest of two numbers, then the largest of three numbers (this is a different subtask), then the largest of four, five, six, seven - stop when you understand that you are not following a rational path and for larger quantities you should do it differently. Complete the task only using the conditional operator if().
Here, let's begin by finding the largest number for small sets, increasing the count each time. Let's start with the largest.
The Largest of Two Numbers
This is a straightforward approach, which we can compare two numbers and returns theargest using a single if statement as shared 👇 below.
#include <iostream>
using namespace std;
int largestOfTwo(int a, int b) {
if (a > b) return a;
else return b;
}
int main() {
int a = 10, b = 20;
cout << "Largest of two: " << largestOfTwo(a, b) << endl;
return 0;
}
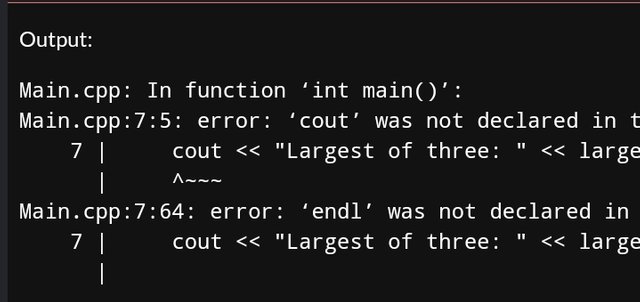
The Largest of Three Numbers:
In order for we to find the largest of three numbers, we will have to first compare two of them, and then compare the result with the their number.
int largestOfThree(int a, int b, int c) {
int largest;
if (a > b) largest = a;
else largest = b;
if (c > largest) largest = c;
return largest;
}
int main() {
int a = 10, b = 20, c = 15;
cout << "Largest of three: " << largestOfThree(a, b, c) << endl;
return 0;
}
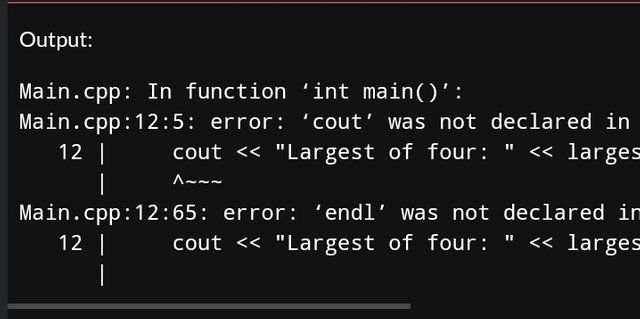
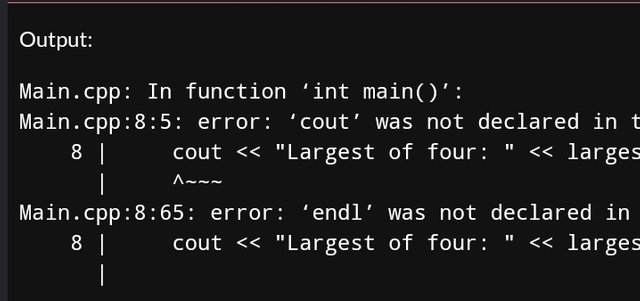
The Largest of Four Numbers
int largestOfFour(int a, int b, int c, int d) {
int largest;
if (a > b) largest = a;
else largest = b;
if (c > largest) largest = c;
if (d > largest) largest = d;
return largest;
}
int main() {
int a = 10, b = 20, c = 15, d = 25;
cout << "Largest of four: " << largestOfFour(a, b, c, d) << endl;
return 0;
}
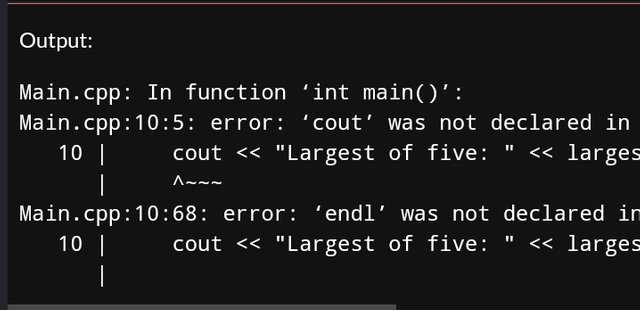
The Largest of Five, Six etc.
For this approach we will have to increase the number of variables, writing each condition manually cab become increasingly and full of errors.
With five numbers it would looks as shared below.
int largestOfFive(int a, int b, int c, int d, int e) {
int largest;
if (a > b) largest = a;
else largest = b;
if (c > largest) largest = c;
if (d > largest) largest = d;
if (e > largest) largest = e;
return largest;
}
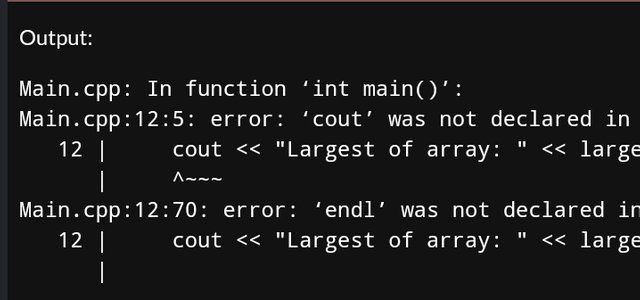
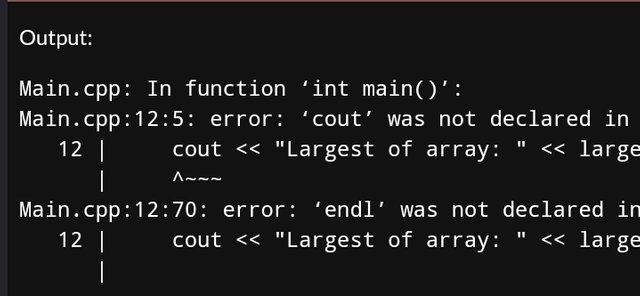
For a more larger numbers we can make use of an array and iterate through it to find the element that is the largest. This minimise the code to a simple loop structure, which we can also handle quanttot numbers using this approach. Let's take a look at the code below.
int largestOfArray(int arr[], int size) {
int largest = arr[0]; // Start with the first element
for (int i = 1; i < size; i++) {
if (arr[i] > largest) largest = arr[i];
}
return largest;
}
int main() {
int numbers[] = {10, 20, 15, 25, 30, 5, 40}; // Array of any size
int size = sizeof(numbers) / sizeof(numbers[0]);
cout << "Largest of array: " << largestOfArray(numbers, size) << endl;
return 0;
}
Interpretation
Initialising is the
largestto the first element of the array.Loop: Through this the updating
largesteach time a larger element is found can be done easily through array.ifstatement is what the approach make use of.
Perform the previous task using the ternary operator.
What we are going to do here, is to go through each case so we can find the largest number using ternary operator. It is an operator allows us someone to condense conditional logic, that will streamline comparison for each case.
Largest of Two Numbers
#include <iostream>
using namespace std;
int largestOfTwo(int a, int b) {
return (a > b) ? a : b;
}
int main() {
int a = 10, b = 20;
cout << "Largest of two: " << largestOfTwo(a, b) << endl;
return 0;
}
Largest of Three Numbers
int largestOfThree(int a, int b, int c) {
return (a > b) ? ((a > c) ? a : c) : ((b > c) ? b : c);
}
int main() {
int a = 10, b = 20, c = 15;
cout << "Largest of three: " << largestOfThree(a, b, c) << endl;
return 0;
}
Largest of Four Numbers
int largestOfFour(int a, int b, int c, int d) {
return (a > b) ? ((a > c) ? ((a > d) ? a : d) : ((c > d) ? c : d))
: ((b > c) ? ((b > d) ? b : d) : ((c > d) ? c : d));
}
int main() {
int a = 10, b = 20, c = 15, d = 25;
cout << "Largest of four: " << largestOfFour(a, b, c, d) << endl;
return 0;
}
Largest of Five, Six, and Seven Numbers
int largestOfFive(int a, int b, int c, int d, int e) {
return (a > b) ? ((a > c) ? ((a > d) ? ((a > e) ? a : e) : ((d > e) ? d : e))
: ((c > d) ? ((c > e) ? c : e) : ((d > e) ? d : e)))
: ((b > c) ? ((b > d) ? ((b > e) ? b : e) : ((d > e) ? d : e))
: ((c > d) ? ((c > e) ? c : e) : ((d > e) ? d : e)));
}
int main() {
int a = 10, b = 20, c = 15, d = 25, e = 30;
cout << "Largest of five: " << largestOfFive(a, b, c, d, e) << endl;
return 0;
}
Drawback
The issue with the ternary operator is that using it for larger sets of numbers is difficult to read due to deep nesting, which makes code to become difficult to maintain.
Solution
The use of array and a loop is much better for a larger sets of numbers than the use of ternary operator which if we should make use of an array and a loop will would get to find the largest number more effectively.
int largestOfArray(int arr[], int size) {
int largest = arr[0];
for (int i = 1; i < size; i++) {
largest = (arr[i] > largest) ? arr[i] : largest;
}
return largest;
}
int main() {
int numbers[] = {10, 20, 15, 25, 30, 5, 40};
int size = sizeof(numbers) / sizeof(numbers[0]);
cout << "Largest of array: " << largestOfArray(numbers, size) << endl;
return 0;
}
Perform the previous task by writing a function max() and using it.
For we to make the code more modular and reusable we will need to write a max() function that takes two integers and returns the larger one.
Step 1: Define the max() Function
The max() function is the function that takes two numbers as input and returns the larger one as seen in the code below 👇.
int max(int a, int b) {
return (a > b) ? a : b;
}
Step 2: Using max() to find the largest of multiple Numbers
Also, with the max() function, we can find the largest of two, three, four, five, six, seven, or more numbers by chaining max() calls.
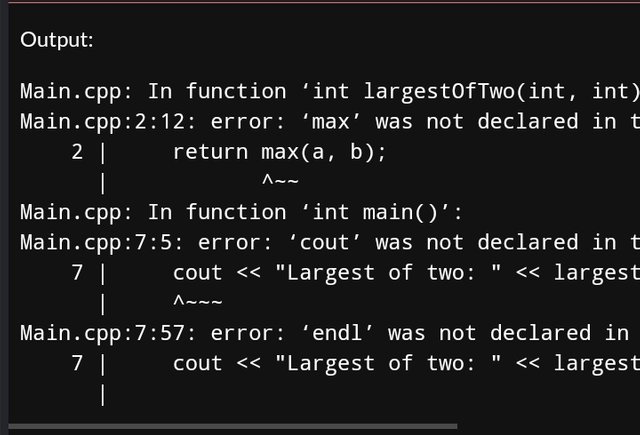
Largest of Two Numbers
int largestOfTwo(int a, int b) {
return max(a, b);
}
int main() {
int a = 10, b = 20;
cout << "Largest of two: " << largestOfTwo(a, b) << endl;
return 0;
}
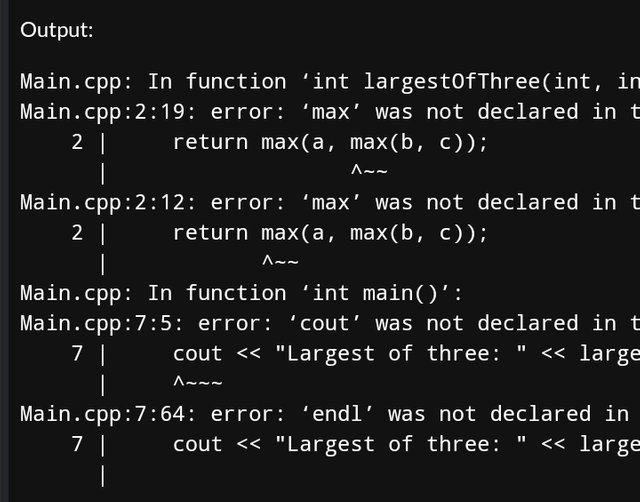
Largest of Three Numbers
int largestOfThree(int a, int b, int c) {
return max(a, max(b, c));
}
int main() {
int a = 10, b = 20, c = 15;
cout << "Largest of three: " << largestOfThree(a, b, c) << endl;
return 0;
}
Largest pt Four Numbers
int largestOfFour(int a, int b, int c, int d) {
return max(a, max(b, max(c, d)));
}
int main() {
int a = 10, b = 20, c = 15, d = 25;
cout << "Largest of four: " << largestOfFour(a, b, c, d) << endl;
return 0;
}
Largest of Five, Six, Seven, or More Numbers
int largestOfFive(int a, int b, int c, int d, int e) {
return max(a, max(b, max(c, max(d, e))));
}
int main() {
int a = 10, b = 20, c = 15, d = 25, e = 30;
cout << "Largest of five: " << largestOfFive(a, b, c, d, e) << endl;
return 0;
}
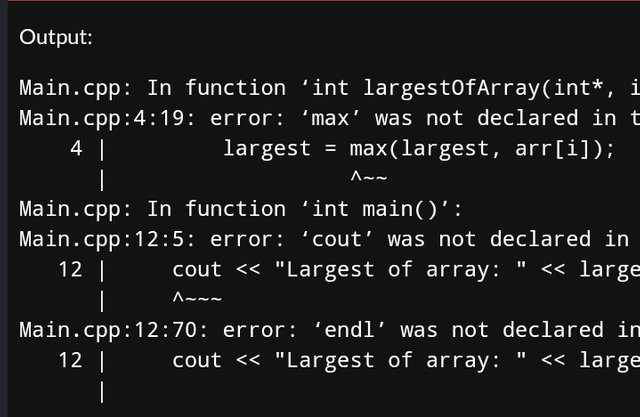
Largest of an Array Numbers
int largestOfArray(int arr[], int size) {
int largest = arr[0];
for (int i = 1; i < size; i++) {
largest = max(largest, arr[i]);
}
return largest;
}
int main() {
int numbers[] = {10, 20, 15, 25, 30, 5, 40};
int size = sizeof(numbers) / sizeof(numbers[0]);
cout << "Largest of array: " << largestOfArray(numbers, size) << endl;
return 0;
}
Interpretation
max()Function: this is the function that compares two numbers and returns the larger number.Chaining
max()Calls: this is use to reduce multiple numbers of the largest one.Loop for Large Sets: For an array
largestis initialised with the first element, and then loop through each element, updatinglargestusing themax()function.
Write functions: that will print all the divisors of a given number print_div(number) - you can skip printing one and the number itself print_div(11) => (empty), print_div(12) => 2 3 4 6 a function sum_div(number) that will calculate the sum of its divisors that are less than itself sum_div(6) = 1+2+3=6, sum_div(10) = 1+2+5=8,
a function that will find and print perfect numbers from 1 to n (the number passed to the function) perfect numbers are those where the sum of divisors less than the number equals the number itself.
First let's start by looking at the implementation of each function according to the requirements:
print_div(number): This function will help us to print all divisors ofnumber, excluding1andnumberitself.sum_div(number): This function will help us return the sum of all divisors ofnumberthat are less thannumberitself.print_perfect_numbers(/: This function will help us to print all perfect numbers between1andn. Let's take a look at the code 👇 below.
#include <iostream>
using namespace std;
// Function to print divisors of a number excluding 1 and the number itself
void print_div(int number) {
bool hasDivisors = false; // Flag to check if any divisors were found
for (int i = 2; i <= number / 2; i++) { // Start from 2 and go up to half of the number
if (number % i == 0) { // If `i` divides `number` evenly, it's a divisor
cout << i << " ";
hasDivisors = true;
}
}
if (!hasDivisors) cout << "(empty)"; // Print (empty) if no divisors were found
cout << endl;
}
// Function to calculate the sum of divisors of a number that are less than itself
int sum_div(int number) {
int sum = 0;
for (int i = 1; i < number; i++) { // Go through all numbers less than `number`
if (number % i == 0) { // If `i` is a divisor, add it to `sum`
sum += i;
}
}
return sum;
}
// Function to find and print perfect numbers from 1 to n
void print_perfect_numbers(int n) {
for (int i = 1; i <= n; i++) {
if (sum_div(i) == i) { // If the sum of divisors equals the number itself, it's perfect
cout << i << " ";
}
}
cout << endl;
}
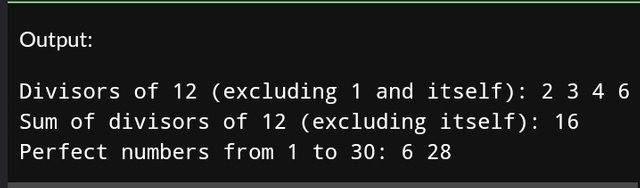
int main() {
int number = 12;
cout << "Divisors of " << number << " (excluding 1 and itself): ";
print_div(number);
cout << "Sum of divisors of " << number << " (excluding itself): " << sum_div(number) << endl;
int n = 30;
cout << "Perfect numbers from 1 to " << n << ": ";
print_perfect_numbers(n);
return 0;
}
Interpretation
print_div(number):
- Loops from
2tonumber / 2as divisors cannot be divisors than the number itself. - If no divisors are found it prints
empty - Prints each divisors found, excluding
1andnumber.
sum_div(number):
- Loops through numbers from
1up to excludingnumber - Adds each divisors to
sumif it dividesnumberevenly and return the total sum.
print_perfect_numbers(n):
- Loops through numbers from
1ton sum_div(I)is equal toiis use to check for a perfect number which will then be printed.
I am inviting: @kuoba01, @simonnwigwe, and @lhorgic
All Screenshots used in this post are products of mine which are all gotten from one Compiler Editor
Cc:-
@sergeyk



Congratulations, your post has been upvoted by @scilwa, which is a curating account for @R2cornell's Discord Community. We can also be found on our hive community & peakd as well as on my Discord Server
Felicitaciones, su publication ha sido votado por @scilwa. También puedo ser encontrado en nuestra comunidad de colmena y Peakd así como en mi servidor de discordia
Omo programmers really tried ooo 😂
I find it hard to understand all this
You can do it with your determination.
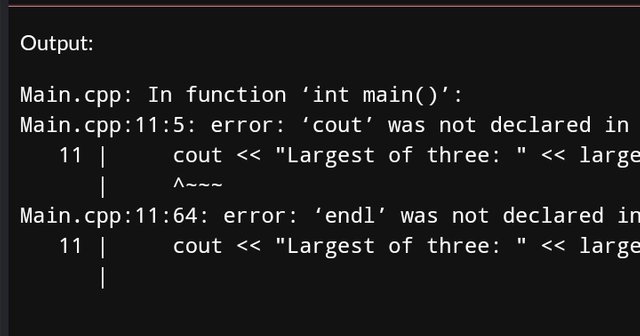
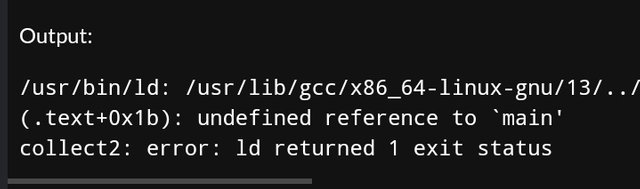
half of the tasks do not compile, give an error. Why are you reporting on unsolved tasks? It was necessary to understand what the error was and eliminate it. And in the task I asked for screenshots of the code, not the text of the code.
Well, since I didn't use my system (PC) to run the code, because my system is faulty which I took for repair, I thought sharing the code would be helpful because screenshotting it via phone to share wouldn't be fully displayed. Thanks for your suggestions
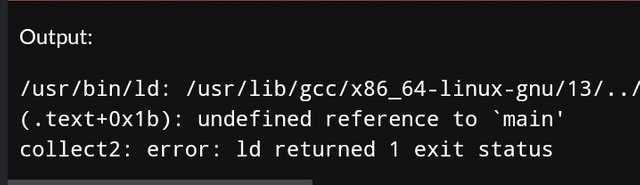
the problem is different, the code doesn't compile, so you can't check if the program is correct or not. for example, you get an error on
cout, then you should either writestd::coutor at the beginning of the program writeusing namespace stdIn other tasks, you compile a part of the code, not the whole program, and you see a message that there is no main() function, while it is required
Can I really still catch up with all of these coding things...A good system is my limiting factor, maybe when I get one soon, I would join you in this contest... BTW you did excellently well with this entry of yours. Weldon boss.
It is easier to learn sir.