빙구처럼 트레이딩: 코인 차트 "처음부터" 공부하기 #47- 3단 변신 보조 지표 I (Relative ATR)
저번에 절대 변동성 값을 표현하는 ATR 을 비율로 나타내는 상대 값으로 변환하는 조작을 해주었습니다. 아쉽게도 저번 지표에서는 수익률에 변동성이 크게 영향을 미치지 않았는지, 만들어놓고 사용하지 않게 되었죠. ㅠㅠ 이번에는 이 상대 변동성을 활용하여 실험적인 연구를 해 볼 예정입니다!
그리고 이 ATR 로 나눈 세 구간에 대하여, 익절, 손절값을 다르게 설정하여 이전에 구간별 손절 선이 벌어졌다 좁아졌다를 한 단계 확장 시켜, 세 구간에 대하여 손절선과 익절선이 움직이는 관점으로 접근해보겠습니다.
복습
먼저 저는 ATR 을 변동성으로 사용한다는 사실은 전부 아실거고! ATR 을 활용하는데 있어서 문제점은 절대적이라는 점 입니다.
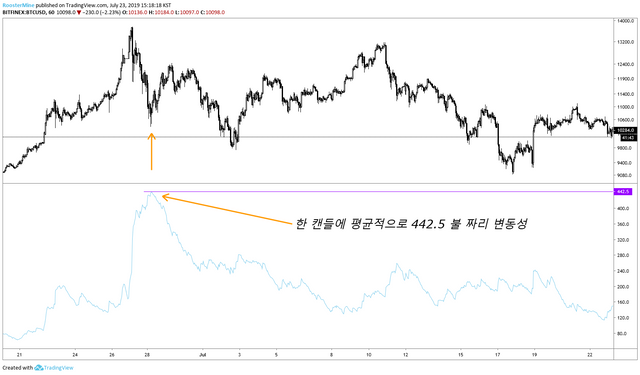
만 불 일때 442.5불의 변동성이랑, 천 불 일때 442.5불의 변동성은 10 배 차이기 때문이죠. 그러기에 이 절대 ATR 값을 상대 ATR 값으로 바꾸는 조작을 해줍니다.
ATRinput = input(20)
Relative = atr(ATRinput) / sma(close, ATRinput) *100
이런식으로 ATR 주기를 정의해주고, ATR 값을 현재 가격의 평균으로 나눠 줌으로, 현재 평균 가격 대비 평균 변동성이 어떤가를 알아볼 수 있습니다.
그리고 100을 곱해줌으로써 퍼센트로 표현하여 보기 쉽게 바꿔주었습니다.
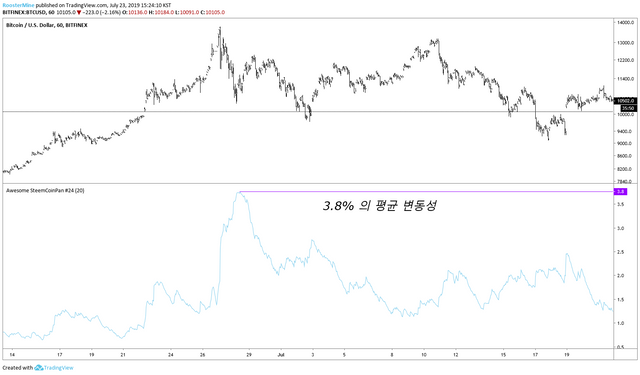
이제 442.5 불의 변동성에서 3.8%의 변동성으로 바꿔줄 수 있습니다. 오늘은 이런 퍼센트 값을 활용하여 여러 실험을 해보겠습니다.
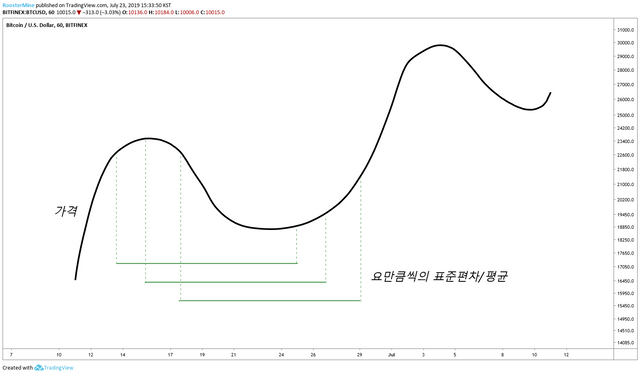
표준 편차
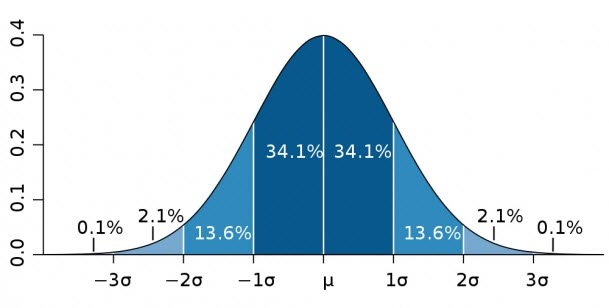
다들 한 번씩 들은 이런 종 모양을 보셨을 겁니다! 값들이 어떻게 분포해 있나 를 봤을때 평균을 기준으로 표준편차 (시그마) 안에 대충 70% 의 값들은 정도는 들어간다 라는 뜻 입니다. 물론 가격 데이터가 엄밀하게 정규 분포를 따르진 않겠지만, 극점을 찾는데에는 어느정도 도움이 될 거라고 믿기에 실험적으로 접근해보겠습니다!
RelativeMA = sma(Relative, 20)
일단 표준편차를 구하기 전에 평균 부터 구합니다. 보통은 값을 정규화 시켜서 스케일을 고정시키지만, 저희는 스케일을 옮겨서 값을 분석하게 되는 거죠!
plot(RelativeMA, color=red)
그리고 그리면
요런 평균 값들이 나옵니다.
ATRstdeva = stdev(Relative,ATRinput )
그리고 상대값들의 표준 편차를 ATRinput (설정값 20) 주기 동안 발생한 값들로 구해줍니다.
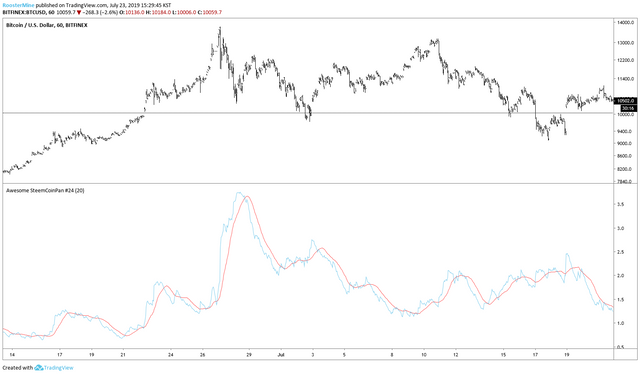
이런 느낌 입니다. 하지만, 사용 가치가 있을지 없을지는 모르겠는게, ATR 값 자체에서 이미 한 번 20 주기에 대한 값을 뭉게서 나타내고, 또 ATR 을 20 주기로 평균을 내려버리면 음.... 일단 실험적 이니깐, 오차를 감안하고 생각해봐야 겠습니다.
BandH = RelativeMA + ATRstdeva
BandL = RelativeMA - ATRstdeva
plot(BandH, color= green)
plot(BandL, color= green)
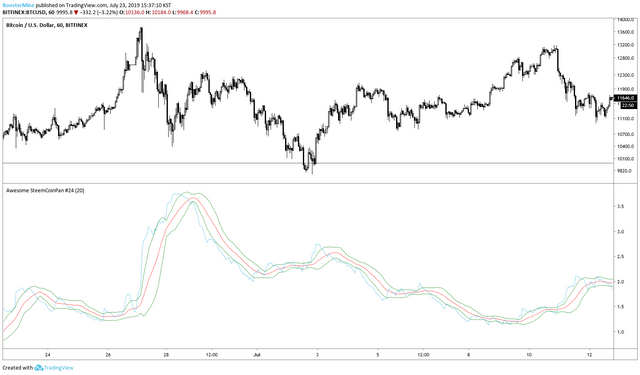
그리고 이동평균에 표준 편차를 더하고 뺀 값에 대한 변수를 지정해주고, 차트에 그려줍니다. 선 색깔은 춰럭색으로!
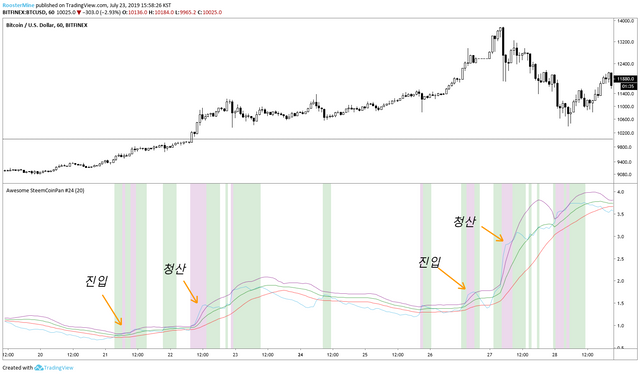
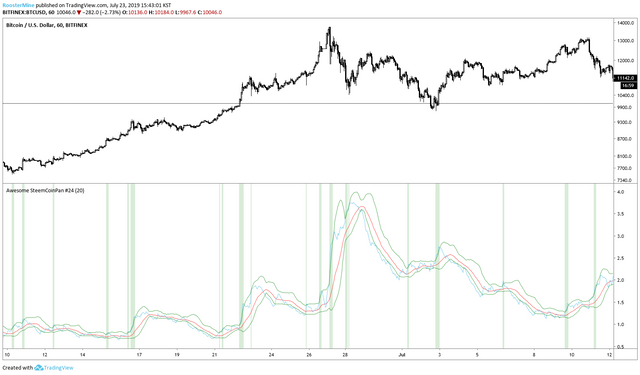
이렇게 잘게 자르면, 네 구간, 벤드를 하나로 보면 세 구간으로 나눌 수 있는 네 가지의 선들이 나옵니다.
이제 선들의 배열에 따라 표시를 다르게 해줘볼께요.
HighR = Relative > BandH
LowR = Relative < BandL
만약 상대값이 밴드보다 높으면 HighR, 상대값이 밴드보다 낮으면 LowR
bgcolor(color = HighR ? green: na, transp = 85)
bgcolor(color = LowR ? red: na, transp = 85)
그리고 그 상태들을 시그널로 표현해줍니다.
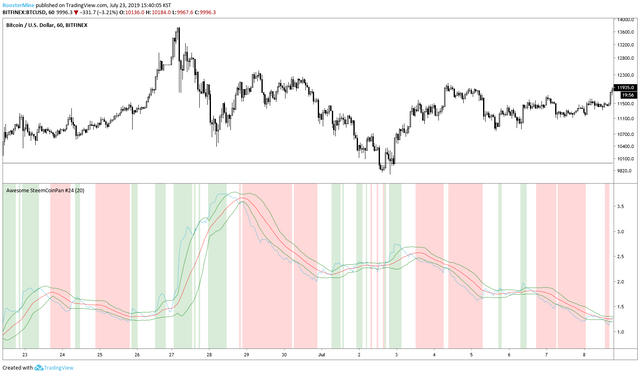
생각보다 무뎌져서 그런지 의미있는 값을 출력하는지 아닌지 모르겠습니다. 저 변동성 구간은 관심 없으니 끄고, 원론적으로 5% 값들만 출력해야 하는 2 표준편차 값으로 수정하여, 진짜 극적인 변동성을 보여줄 때에만 시그널을 발생시켜보겠습니다.
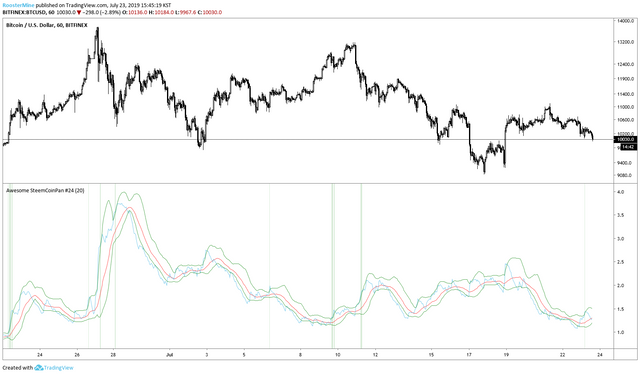
꽤 의미있는 진입 시그널을 보내는 것 같기도하고?.... 일단, 매수 진입에 대한 시그널로 활용을 가정하고, 양봉과 추세항을 추가해보겠습니다.
꽤 시그널을 잘 잡는 것 같기도하구요? 진입은 요걸로 당첨!
이제 구간을 쪼개야 하는데, 1 시그마 값과 2 시그마 값을 커서, 변동성이 극도로 커질때 손절을 극도로 올려 수익을 한 층 더 높이는 방법으로 접근해 볼 거에요!
BandH = RelativeMA + 1ATRstdeva
BandH2 = RelativeMA + 2ATRstdeva
아랫 벤드는 뭐 활용하지 않을 것이니 과감하게 빼버리고,
plot(BandH, color= green)
plot(BandH2, color= purple)
윗 밴드를 보라색으로 바꿔줍니다.
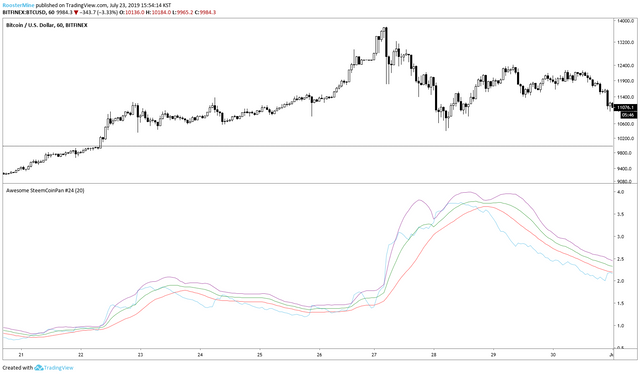
이제 세 구간으로 나뉘게 됩니다.
- 초록색 아래 = 저 변동성
- 초록색과 보라색 사이 = 중 변동성
- 보라색 위 = 고 변동성
아이디어는 진입을 고 변동성에서 하여, 저점에서 급격하게 발생하는 매수세에 탑승하고, 고점에서 발생하는 급격한 매수세에 털고 나오는 것 입니다. (슬프게도 개인 투자자가 가장 많이 진입하는 부분에서 탈출해야 하죠.)
HighR = Relative > BandH and Relative < BandH2
HighR2 = Relative > BandH2
LowR = Relative < BandH
고로 구간을 설정해주고
bgcolor(color = HighR ? green: na, transp = 85)
bgcolor(color = HighR2 ? purple: na, transp = 85)
퍼플로 긴장감이 고조되었다는 점을 강조해줍니다 크흐흫....
제가 원하는 느낌 입니다. 어느정도 비슷하게 나왔으니, 최적화 단계에서 세부적인 조정을 하기로 합니다~
오늘은 일단 상대 변동성을 기준으로 매수 진입의 조건과 가격을 분류해 보았습니다. 다음 시간에는 분류된 가격 별로 어떻게 대응해야 하는지, 손절과 익절을 달아보도록 해요!
질문, 댓글, 팔로우는 감사합니다!
새로운 아이디어, 종목 추천 등은 언제나 환영입니다!