Fraktale - Mathematische Monster
Hier nun eine tatsächliche erste Annäherung an das Thema "Fraktale und Chaostheorie",
die über grundelegende Defintionen von benötigtem Fachvokabular hinausgeht.
Heute betrachten wir erstmals fraktale Objekte.
Einer genaueren Definiton eines "Fraktals" nehme ich mich ein ander Mal an.
Im speziellen betrachten wir hier solche,
die als mathematische Monster in die Geschichte eingegangen sind.
Georg Ferdinand Ludwig Philipp Cantor (dt. Mathematiker 1845-1918) erschuf 1870
eine geometrische Figur, welche später als Cantor-Fraktal bekannt werden sollte,
vorerst aber von Mathematikern, auf Grund ihrer mathematischen Eigenschaften,
als mathematisches Monster bezeichnet wurde.
Diese entsteht durch in dem man eine Linie nach unten kopiert und von dieser kopierten das mittlere Drittel entfernt. Diese neue Zeile wieder nach unten kopiert und erneut von allen Linien das mittlere Drittel entfernt.
Diese Grenzform, die das eigentliche Fraktal ist, erhält man in dem man diese Iterationsvorschrift ad infinitum fortführt.
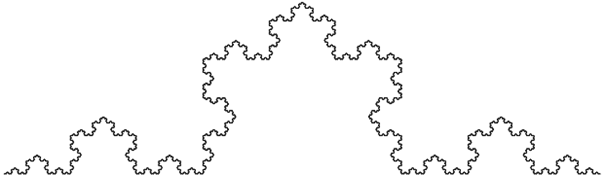
Am Beispiel der Kochkurve die 1904 von Nils Fabian Helge von Koch (sv. Mathematiker 1870-1924) erfunden wurde zeigt sich deutlich, was Gründe dafür waren,
dass diese geometrischen Objekte "mathematische Monster" genannt wurden.
Die Kurve erhält man, in dem man jeweils von allen Linien das mittlere Drittel entfernt und die anderen beiden Ausenlinien des gedachten gleichseitigen Dreicks ergänzt.
Ebenfalls ad infinitum.
Daraus ergibt sich die seltsame Eigenschaft, dass sich an diese Kurve nirgends eine Tangente anlegen lässt.
Zum Abschluss einige weitere berühmte Beispiele:
Minkowski-Fraktal
Hermann Minkowski (dt. Mathematiker/Physiker 1864-1909)
Heighway-Drache/ Drachenkurve
Sierpiński Dreieck
Jedes Dreieck wird durch 4 kongruente gleichseitige Dreiecke ersetzt und das mittlere entfernt.
und Sierpiński Teppich
Jedes Quadrat wird in 9 gleichgroße Quadrate eingeteilt und das Mittlere entfernt.

nach Wacław Franciszek Sierpiński (poln. Mathematiker 1882-1969)
Diese Fraktale können durch graphische Iteration durch die Methoden des wiederholten Entfernens und des wiederholten Substituierens erlangt werden.
Die oben beschriebene Methode die Kochkurve zu erlangen gehört zur Methode des wiederholten Substituierens und Sierpiński's Fraktale werden hier über die Methode des wiederholten Entfernens beschrieben. Oft kann man sie aber auch über die andere Methode erreichen.




.
Freut mich, wenn ich mit meinen Interessen Lücken füllen, informieren und erfreuen kann.
Es gibt fraktale Flächen mit unendlicher Kantenlänge und begrenztem Volumen. Es gibt auch fraktale räumliche Objekte mit ohne Volumen und endlicher Größe. :)
Unsere Küstenlinien sind auch fraktale Muster. Fraktale sparen in der Natur und in der Computertechnik Informationsmenge beim Konstruieren komplexer Gebilde.
Stimmt genau. Die nächste Artikel der "Reihe" wird sich daher vermutlich auch um Küstenlinien drehen.
Die Koch-Kurve kann bspw. als eine ideale mathematische Küstenlinie betrachtet werden.
Das Sirpinski-Dreieck wäre ein Beispiel für unendliche Länge aber keine Fläche. Das reicht dann aber ins Themengebiet Dimensionen, das ich ebenfalls vorhabe zu behandeln.