I've been thinking about building a tool to help me play Alphabear, so I thought I'd write up some notes on data structures used for word problems. An interesting feature of Alphabear not covered by tools like MoreWords is that you have some letters that you really want to use, and a larger collection of letters that you could use.

Word Signatures

Suppose you want to know if there's any word that can be made out of the letters TGHORILAM, or a subset of its letters. Exploring all the possible ways to rearrange a 9-letter word is a lot: exactly 362,880 possibilities! That's more words than exist in a Scrabble word list, so you'd be better off just checking words one at a time.

However, if you permit a brief excursion into abstract algebra, if A is an anagram of B, and B is an anagram of C, then A is an anagram of C as well. That means anagrams form an equivalence relation on the set of letter strings, grouping them into equivalence classes. And whenever we're dealing with equivalence classes, the thing to look for is whether we can find a "representative" of each class. When we deal with the numbers modulo N, we typically take the numbers 0, 1, 2, 3, ... , N-1 as the representatives of the classes; we can easily find the representative for any other number by taking its remainder after division by N.

We can't divide a set of letters and take the remainder--- any way of doing so would probably lose too much information. But we could create a representative by sorting the letters. This preserves the letters in the string, so the representative is in the right equivalence glass, and it's easy to accomplish.

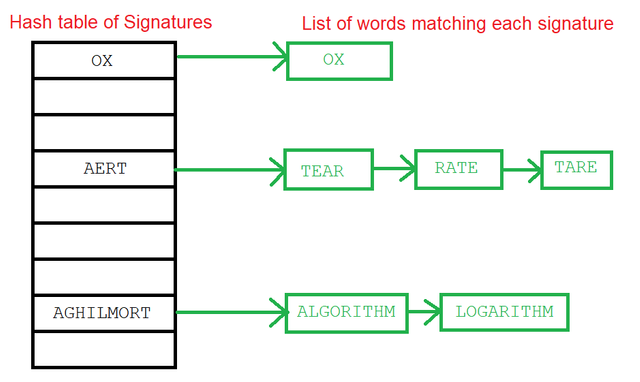
So, one technique for solving anagram problems is to define a representative or "signature" for each word, build a dictionary of signatures as a hash table, and then look up any input word by its signature.

For example, RATE and TEAR, and TARE are all anagrams. If we sort the letters in these words, we get the signature AERT (which is not a word.) But if somebody gives us TRAE as input, we can sort it to AERT and suggest RATE, TEAR, or TARE as valid anagrams.

The cost of looking up any string of letters is very small. A hash table lookup gives us a lookup cost that scales with the number of letters in the input word, rather than with the size of the dictionary. This means we can use the same structure many times and still get done in a short amount of time, as described in the next section.

Sorting is not the only way to produce a unique signature. For example, we could assign each letter a different prime number and multiply the values of the input word. Or, we could represent the signature as a vector with 26 elements, counting the number of times each letter appears. Both of these operations produce a signature that is independent of the original order of the letters.

Smaller and longer words

Suppose we want to use the input letters, plus one extra letter (for example, a letter already on the Scrabble board) to make a word. Using the data structure above, that is pretty simple: we just do 26 lookups, one for each possible letter that may be added.

What about words that are contained in the set of letters we have? This requires a little bit more work. Given an N-letter word, we can perform 2^N-1 searches to find all smaller (or equal-length) words using the same letters. This is most efficient if we convert the input to a signature first, as omitting letters from the signature maintains sorted order. This is the same procedure as enumerating all subsets of a given set, except that our "set" may contain multiple of the same letter. You can also think of it as counting in binary, and including the letters represented by "1"s.

For example, to find smaller words in RATE, convert to the signature AERT again, and then try to find each of the following signatures in the hash table:

T    (0001)
R    (0010)
RT   (0011)
E    (0100)
ET   (0101) 
ERT  (0111) 
A    (1000)
AT   (1001)
AR   (1010)
ART  (1011)
AE   (1100)
AET  (1101)
AER  (1110)
AERT (1111)

We can even combine the two techniques, and add a letter before searching for smaller words. (This is one of the services MoreWords provides.) We should take care not to repeat the same search twice, though: when enumerating smaller words, we should not drop the letter that we specifically added!

At what point, though, does this search become too expensive?

Number of input letters	Smaller word search cost	Smaller word "plus one" search cost
6	63	1638
7	127	3302
8	255	6630
9	511	13286
10	1023	26598
11	2047	53222
12	4095	106470
13	8191	212966
14	16383	425958

Once we get to 13 or 14 input letters, the number of searches we're doing probably exceeds the size of the original dictionary. We might as well just scan through the whole word list looking for matches (which can be done efficiently on two sorted signatures, or even more efficiently on the vector representation.)

Similarly, it we want to add more than 1 letter, it quickly becomes expensive to do so:

Additional letters	Search cost
1	26
2	676
3	17576
4	456976
6	308915776

So if we have a stub and want to expand it with 4 additional letters, cycling through all 26^4 possible additions is too expensive, and we'd be better off just scanning the word list.

Further Reading

There's another structure we can use which lets us solve some additional types of problems, and overcomes the scale limitations for longer words; I'll introduce Tries and suffix tries in part 2.

"What algorithms and data structures can be used to find anagrams", Quora

Wolfram Alpha can solve word puzzles, too.