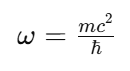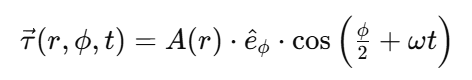¿Qué es una partícula? La materia como torsión contenida del vacío
Introducción
En este post vamos a cambiar el enfoque: después de explorar conceptos como el vacío, la gravedad, la masa y el tiempo, vamos a preguntarnos algo más concreto,
¿Qué es una partícula? ¿Cómo se forma algo tan específico como un electrón, un muón o un protón a partir de un vacío estructurado?
Desde la perspectiva de la torsión estructural del vacío, una partícula no es un objeto separado del vacío, sino una región del mismo que se organiza de manera estable y localizada. Vamos a explorar qué significa eso y cómo podemos describirlo.
El vacío como campo torsional
En esta teoría, el vacío no es nada: es una estructura activa, que tiene una frecuencia mínima natural, una elasticidad interna y una capacidad de autoorganizarse en presencia de energía.
Cuando una porción del vacío se excita por encima de cierto umbral, puede comenzar a torsionarse sobre sí misma. Esta torsión puede ser caótica, transitoria o—bajo condiciones específicas—estabilizarse en una configuración estable.
Ese estado estabilizado, con una frecuencia torsional definida y una forma espacial contenida, es lo que llamamos una partícula.
Cada partícula tiene su propia frecuencia
La torsión del vacío que define una partícula tiene una frecuencia característica:
Esta frecuencia no es arbitraria: está directamente relacionada con la masa de la partícula. Es su "ritmo interno de torsión". Cuanto más masiva la partícula, más rápida es su frecuencia.
Esto implica que una partícula no es una cosa estática, sino una oscilación estructural del vacío en una forma contenida.
El confinamiento de la torsión: cómo se forma el cuerpo de la partícula
No basta con tener una frecuencia: para que una partícula exista, esa torsión tiene que poder sostenerse en el entorno del vacío donde aparece.
Aquí entra en juego el concepto de frecuencia mínima del vacío ω0 :
Si la frecuencia ω de la partícula es menor o igual a ω0 , el vacío puede sostener esa estructura.
Si ω es mayor, la torsión colapsa: la partícula se desintegra.
Así, la existencia de una partícula está condicionada por su compatibilidad estructural con el entorno.
Además, la geometría del campo torsional define un perfil radial: una especie de "envoltura" en la que se contiene la torsión. Este perfil se puede calcular, y su "radio efectivo" depende del equilibrio entre:
La frecuencia de torsión ω ,
La capacidad del vacío de confinar,
Y la autointeracción del campo torsional consigo mismo.
Espín y cobertura angular
El tipo de campo que se torsiona también importa. En el caso del electrón, por ejemplo, usamos un campo vectorial que gira con una simetría particular:
Este tipo de estructura tiene una doble cobertura angular, lo que significa que debe girar 720° para volver a su estado original. Este comportamiento es exactamente el que caracteriza al espín 1/2, y es una propiedad topológica natural de esta torsión.
Conclusión
En este modelo, una partícula es una porción del vacío que se estructura a sí misma de forma estable, con una frecuencia, un espín y una envoltura espacial definidos. Es el vacío mismo, en una forma rítmica y contenida.
Este punto de vista nos permite entender mejor por qué ciertas partículas existen y otras no, por qué algunas son estables y otras se desintegran, y por qué las propiedades cuánticas como el espín no son añadidos, sino consecuencias directas de la geometría torsional del vacío.