Should he jump? (II) - On cartoon mechanics (again)
Again with our falling friend. On my last post I thought about whether jumping right before the rock hit the ground would make our hero survive the fall. Turns out, not much.
After arriving to that conclusion I immediately thought about the next obvious question. How much is not much? Or, how much would it help?
Quantifying the reduction of impact
A simple approach to the question comes working with the energies. The more energy the falling body has before it reaches the ground, the worse the impact, right? Now, remember how energy cannot be made or destroyed but only transformed? Well, both the falling piece of pavement and our friend are transforming their potential energy (the energy from the height due to the gravitational force) into kinetic energy (also into heat and sound and other types but let's not focus on them, they're not that important in this analysis). Yet, the energy for our man's jump comes from 'outside' the system (or actually, from the chemical energy in the man's body from the large pizza he ate before) so, our energy balance would look like this:
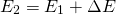
Where E2 is the energy in the system after the jump, E1 the energy before the jump and delta E the energy introduced in the jump.
Now, there's another quantity that conserves itself here: the momentum. Conservation of momentum says that the momentum before and after the jump must be the same so, taking pr and ph as the momenta of the rock and of the human before the jump and pr' and ph' the momenta after the jump, we have:
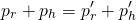
Since the individual momentum for each body does change (the man transfers momentum to the rock) we can write each p' in terms of the previous momentum plus the variation, as such:
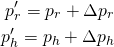
hence:
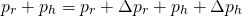
From which we can conclude that the variation on the momenta are equal but opposite (let's remember linear momentum is a vector). We can now define the variation on the momenta as:
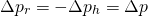
Now, back to our energy balance, writing the energy in terms of the linear momentum, we have:
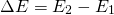
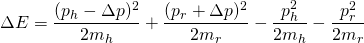
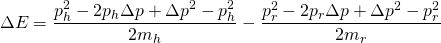
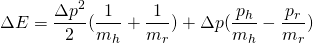
Now, since we're making the assumption both the man's and the rock's velocity is the same before the jump, and linear momentum is defined as p=mv, we can see that the second term on the right hand on the last equation equals zero. Hence:
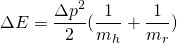
Now, we could follow from there, but I'll make the consideration that the man's mass is much smaller than the rock's mass. So:
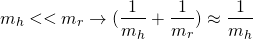
Which allows us to write:
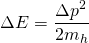
Let's now call Eh' the energy of the human before the impact after he jumps, and Eh the energy he'd have if he didn't. It's easy to see that:
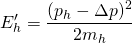
We can also write ph and delta p as:
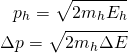
Substituting both in the previous equation we have:
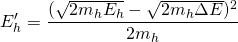
And finally:
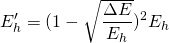
Since kinetic energy dominates the problem according to all the assumptions, we can say that the relation between the energies is similar to that of the squares of the velocities, so:
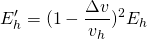
And so we have a relation between the energy withstood with the jump (Eh') and the energy withstood without it (Eh)!!
PD: Notice we could've arrived at a similar conclusion by writing the kinetic energy in terms of the mass and the velocities and determining the relation of the energy both in the case he jumps and in the case he doesn't. Part of the beauty of all this.
Putting in some numbers!
This has been extensive enough, I believe, so I'll wrap it up with some numerical values. (See the previous post for a the free fall velocity calculus and the jumping velocity estimation).
Let's study the case in which he falls from a height of 100 meters:
Now, for a more optimistic situation, let's say he's falling from 10 meters instead:
Closing
While this is really fun to ponder and try to answer with mathematical and physical relations, it's still really rough (not taking into consideration a lot of factors as stated in the previous post), so take it with a pinch of salt.
Also, my overall conclusion is that it is not a good idea to stand in falling pieces of concrete plunging toward a random hole in the floor. At all.
The equations were written using quicklatex, very convenient tool.
Please let me know what you thought about all this and any errors you might find in both the reasoning and the math involved (or the definitions). Thanks for reading!
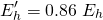
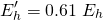
Congratulations @isa93! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPCongratulations! This post has been upvoted from the communal account, @minnowsupport, by Isa [Chicken Chaser] from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, theprophet0, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.