Explanations of mathematical science - Integration
Hello friends, continuing with my series of publications, today in this publication I am going to make reference to the integration, which is a mathematical procedure that is present in our daily life since it calculates the difference of time as a function of speed, and based on this mathematical calculation you can know many properties related to this magical lamatematica, I invite you to observe this interesting article!
Welcome to this magical world of mathematical sciences ....
The Integration
Integration is a fundamental concept of calculation and mathematical analysis. Basically, an integral is a generalization of the sum of infinite addends, infinitely small.
The integral calculus, framed in the infinitesimal calculus, is a branch of mathematics in the process of integration or antiderivation. It is very common in engineering and science; It is mainly used for the calculation of areas and volumes of regions and solids of revolution.
It was used for the first time by scientists such as Archimedes, René Descartes, Isaac Newton, Gottfried Leibniz and Isaac Barrow. The works of the latter and the contributions of Newton generated the fundamental theorem of integral calculus, which proposes that derivation and integration are inverse processes.
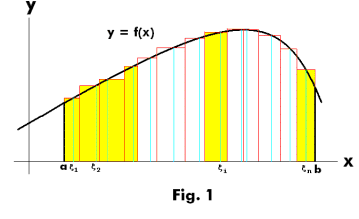
The definite integral of a function represents the area limited by the graph of the function, in a Cartesian coordinate system with a positive sign when the function takes positive values and a negative sign when it takes negative values.
Theory
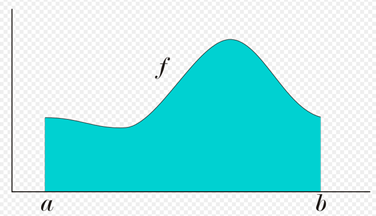
Given a function f (x) of a real variable x and a range [a, b] of the real line, the integral is equal to the area of the region of the xy plane and limited between the graph of f, the x axis, and the lines verticals x = ayx = b, where the areas below the x axis are negative.
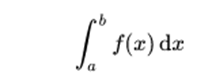
The word "integral" can also refer to the notion of primitive: a function F, whose derivative is the given function f. In this case it is called indefinite integral, while the integrals treated in this article are the defined integrals. Some authors maintain a distinction between primitive and indefinite integrals.
The principles of integration were formulated by Newton and Leibniz at the end of the 17th century. Through the fundamental theorem of calculus, which the two developed independently, the integration is connected to the derivation, and the definite integral of a function can be easily calculated once an antiderivative is known. Integrals and derivatives became basic calculation tools, with numerous applications in science and engineering.
Properties of the integration
###Linearity
- The set of Riemann functions integrable in a closed interval [a, b] form a vector space with the addition operations (the sum function of two others is the function that corresponds to the sum of the images of this point at each point for each of the other two) and multiplication by a scalar. The integration operation.
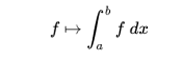
It is a linear functional of this vector space. Thus, first of all, the set of integrable functions is closed with the linear combination, and secondly, the integral of a linear combination is the linear combination of the integrals,
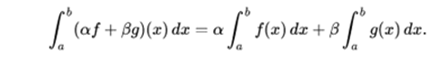
- Similarly, the set of real Lebesgue functions integrable in a given metric space E, with the measure μ is closed with respect to the linear combinations and therefore form a vector space, and the integral of Lebesgue
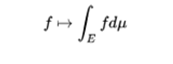
is a linear functional of this vector space, so that
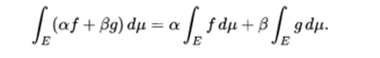
- More generally, if we take the vector space of all the measurable functions on a metric space (E, μ), which take values in a fully compact local topological vector space V over a locally compact topological field K, f: E → V. Then you can define an abstract integration application that assigns each function f an element of V or the symbol ∞,
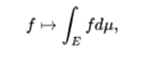
which is compatible with linear combinations. In this situation, linearity is held for the subspace of the functions, whose integral is an element of V (that is, the "finite" integrals). The most important cases arise when K is R, C, or a finite extension of the field Qp of p-adic numbers, and V is a vector space of finite dimension on K, and when K = C and V is a complex Hilbert space .
Linearity, along with some natural properties of continuity and normalization for certain classes of "simple" functions, can be used to give an alternative definition of integral.
Multiple integration
The integrals can be calculated over different regions of the intervals. In general, an integral on a set E of a function f is written:
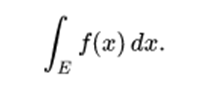
Here x need not necessarily be a real number, but it can be any other appropriate quantity, for example, a vector of R3. Fubini's theorem shows that these integrals can be rewritten as an iterated integral. In other words, the integral can be calculated by integrating the coordinates one by one.
In the same way that the definite integral of a positive function represents the area of the region enclosed between the graph of the function and the x-axis, the double integral of a positive function of two variables represents the volume of the region between the surface defined by the function and the plane that contains its domain. (The same volume can be obtained through a triple integral - the integral of the three-variable function - of the constant function f (x, y, z) = 1 on the region mentioned above between the surface and the plane, the same it can be done with a double integral to calculate a surface.) If the number of variables is greater, then the integral represents a hypervolume, the volume of a solid of more than three dimensions that can not be represented graphically.

Surface integrals
A surface integral is a definite integral calculated on a surface (which can be a set curved in space, it can be understood as the double integral analogous to the line integral.) The function to be integrated can be a scalar field or a vector field The value of the surface integral is the weighted sum of the field values at all points on the surface.This can be achieved by dividing the surface into surface elements, which provide the partition for the Riemann summations. .

The definition of surface integrals rests on the division of the surface into small surface elements.
As an example of the applications of the surface integrals, we can consider a vector field v on a surface S; that is, for each point x of S, v (x) is a vector. Imagine that you have a fluid flowing through S, so that v (x) determines the velocity of the fluid at point x. The flow rate is defined as the amount of fluid flowing through S in the unit of time. To find the flow, we must calculate the scalar product of v by the normal unit vector to the surface S at each point, which will give us a scalar field, which we integrate on the surface:
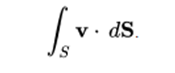
The fluid flow rate of this example may be of a physical fluid such as water or air, or of an electric or magnetic flow. Thus, surface integrals have applications in physics, particularly in the classical theory of electromagnetism.
References and notes
- http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.86.8362&rep=rep1&type=pdf
- http://www.project2061.org/publications/designs/dod/dsl_text/Reprints/8_Davisn.pdf
- http://math.unipa.it/~grim/21_project/21_charlotte_Berlin%20PaperEdit.pdf
- https://vtechworks.lib.vt.edu/bitstream/handle/10919/51614/CTTEv441995TSMIntegration.pdf;sequence=1
Bibliography
- Apostol, Tom M. (1967). Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra (2nd edition). John Wiley & Sons. .
- Bourbaki, Nicolas (2004). Integration I. Springer.. In particular chapters III and IV.
- Burton, David M. (2005). The History of Mathematics: An Introduction (6th edition). McGraw-Hill. p. 359
- Cajori, Florian (1929). A History Of Mathematical Notations -Volume II. Open Court Publishing. pp. 247-252.
- Dahlquist, Germund; Björck, Åke (forthcoming). «Chapter 5: Numerical Integration». Numerical Methods in Scientific Computing. Philadelphia: SIAM. Archived from the original on June 15, 2007.




Hello,
We have found similar content: https://steemit.com/mathematics/@joseferrer/mathematical-explanation-the-integration
Not indicating that the content you post including translations, spun, or re-written articles are not your original work could be seen as plagiarism.
These are some tips on how to share content and add value:
Repeated plagiarized posts are considered spam. Spam is discouraged by the community, and may result in action from the cheetah bot.
If you are actually the original author, please do reply to let us know!
Thank You.
More Info: Abuse Guide - 2017.
TIP: Users plagiarizing the content of other Steemians make great @cheetah chow.
Hi! I am a robot. I just upvoted you! I found similar content that readers might be interested in:
https://steemit.com/mathematics/@joseferrer/mathematical-explanation-the-integration
Nice post! I am an engineering student so I know this topic.
Hard sometimes but at the same time important.
Following you!
Congratulations @titoalbornoz! You received a personal award!
Happy Birthday! - You are on the Steem blockchain for 1 year!
Click here to view your Board
Congratulations @titoalbornoz! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!