Elements of Set Theory: Functions
In most calculus books a function is introduced as a rule that assigns to each object in a certain set (domain) a unique object in a possibly different set (range).
The action of this function can be described by writing,
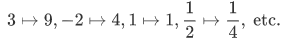
Each individual action can be represented by an ordered pair:
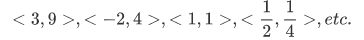
The set of all these pairs represents the squaring function. These set of pairs at times has been called the graph of the function; it is a subset of the coordinate plane 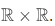 .
.
Thus a function is a set of ordered pairs (i.e., a relation). But it has a special property: it is "single-valued" such that for each domain there is a unique y such that 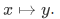
Definition A function is a relation F such that for each x in dom F there is only one y such that 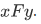
For a function F and a point x in dom F, the unique y such that 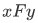 is called the value of F at x and is denoted
is called the value of F at x and is denoted 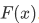 .
.
The "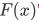 " notation was introduced by Euler in the 1700s.
" notation was introduced by Euler in the 1700s.
Functions are basic objects appearing in all parts of mathematics. Thus, there are many terminologies associated with functions. Unfortunately, no terminology has become uniformly standardized. In this section, we will collect some of this terminology.
Mapping
F is a function from A into B or that F maps A into B written as,
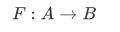
iff F is a function, dom F = A, and ran 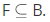 .
.
A special case of range such that ran F = B, then F is a function from A onto B.
Injection
A function F is one-to-one iff for each 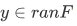 there is only one x such that
there is only one x such that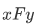 . One-to-one functions are sometimes called injections. Another way to call a one-to-one is to use the phrase "single-rooted", in analogy to "single-valued".
. One-to-one functions are sometimes called injections. Another way to call a one-to-one is to use the phrase "single-rooted", in analogy to "single-valued".
Definition A set R is single-rooted iff for each  there is only one x such that
there is only one x such that 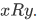 .
.
We can then say that a function is single-rooted iff it is one-to-one.
Consider the following function called "addition", 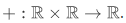 . The domain of addition is consists of pairs of numbers
. The domain of addition is consists of pairs of numbers 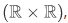 and the addition function itself consists of triples of numbers.
and the addition function itself consists of triples of numbers.
Now, we'll discuss some commonly applied operations to functions, using some defined arbitrary sets 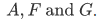
Definition
a. The inverse of F is the set
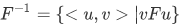
b. The composition of F and G is the set
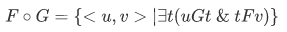
c. The restriction of F to A is the set
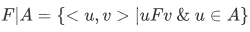
d. The image of A under F is the set
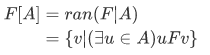
Facts about Functions
Theorem 3E For a set F, dom 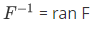 and ran
and ran 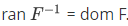 . For a relation F,
. For a relation F, 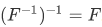 .
.
Theorem 3F For a set F, 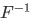 is a function iff F is single-rooted. A relation F is a function iff
is a function iff F is single-rooted. A relation F is a function iff 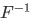 is single-rooted.
is single-rooted.
Theorem 3G Assume that F is a one-to-one function. If 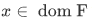 then
then 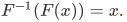 . If
. If 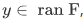 then
then 
Theorem 3H Assume that F and G are functions. Then 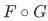 is a function, its domain is
is a function, its domain is
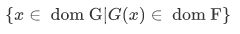
The thing about our definition is that we want them to be general such that they are applicable even to nonfunctions.
Theorem 3I For any sets F and G,
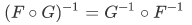
This theorem expresses common knowledge. In getting dressed, one first put on socks and then shoes. But in the inverse process of getting undressed, one first removes shoes and then socks.
Theorem 3J Assume that 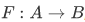 , and that A is nonempty.
, and that A is nonempty.
a) There exists a function 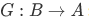 such that
such that 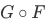 ("left inverse") is the identity function
("left inverse") is the identity function 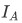 on A iff F is one-to-one.
on A iff F is one-to-one.
b) There exists a function 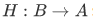 such that
such that 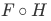 $ ("right inverse") is the identity function
$ ("right inverse") is the identity function 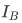 on B iff F maps A onto B.
on B iff F maps A onto B.
Axiom of Choice: (first form) For any relation there is a function 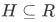 with
with 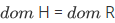 .
.
Corollary 3L For any function 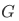 and sets
and sets 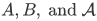 :
:
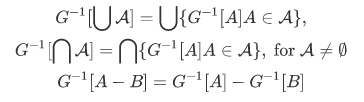
We conclude our discussion of functions with some definitions that may be useful later. Out intent is to build a large working vocabulary of set-theoretic notations.
Consider an infinite union  . We call I the index set. Let F be a function whose domain includes I. Then we define
. We call I the index set. Let F be a function whose domain includes I. Then we define
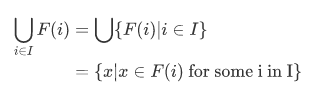
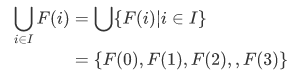
Disclaimer: this is a summary of section 3.4 from the book "Elements of Set Theory" by Herbert B. Enderton, the content apart from rephrasing is identical, most of the equations are from the book and the same examples are treated. All of the equation images were screenshots from generated latex form using typora
Thank you for reading ...


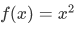
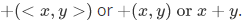
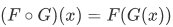
You got a 29.41% upvote from @moneymatchgaming courtesy of @sinbad989! Please consider upvoting this post to help support the MMG Competitive Gaming Community.
You got a 15.38% upvote from @whalepromobot courtesy of @sinbad989!