Determination of the concentration of hands.

I will try here, how to calculate the square root of any integer integers, that is to say the beginning of the rule and then from there to find out the rules of the solid. Then the interested ones can find the n-root, and some instructions will be given.
Rules of class and behind it:
The actual thing is the same thing (10a + b) ² = 100a² + 20ab + b²
Any positive integer number with multiple digits can be written as (10a + b). For example 23 can be written 10 × 2 + 3 Again 113 can be written 10 × 11 + 3 Keeping this in mind, we pay attention to the square root rules.
Suppose we want to find out the square root of 169.

1.Create groups from right to right from two to two houses. Each mark with a mark on each group. 69 groups one and 1 group. To make two, think of it 01 and think. Notice, starting from the end of the group. 16 and 9, the group will not be created but! As a mark is given at the time of sharing, I have given a mark on the right. Where we had a stake in the right of the stain, now we will place our square root, the place that we now say is the place of our square root (the solid solid place in the solid state).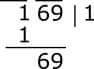

2.Look at the first group - see inside of the largest number of squares. At the right place, we will write that number and at the bottom of the group we write the number of the number. Here 1 is the square of 1 inside 1. Like the share, subtract the following from the above number and write a downward trajectory. Let's next group down. For example, excluding 1 to 1 is zero, I have not written it. Then the group next to 69 was.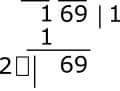

3.On the left side of the division, give a stain like a division. There I will write twice the amount of the square root, and place a blank space beside it. Here square place was 1. So I wrote twice as 2. We have a place like box next to 2.
4.This is the most worrying part now. In that empty space, you have to put such a number that if you multiply the whole number by it, then that is the result of the negative, here it goes in the 69's. An example can be understood well.
First let's sit in the blank room. If you put 1 next to 2, 21 and 21 will give it again. Pub 21 × 1 = 21, it is smaller than 69. But nothing greater than 1 and 69 goes inside? let's see! I would like to show the following in the table below if I have 1, 2, and 3 in the empty room.

Or, it's going to be 69 at 3 in the empty house, it's going to mix with our balance.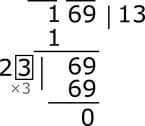

That means that sitting in the blank room will be 3. Place this 3 in the square root of 1, and you get the square of the whole number. That means 13 is our square root. See the whole process in the next picture.
What is the real incident:
To understand what the facts really are, I show two things in the table below: The square that I just made and its algebraic form.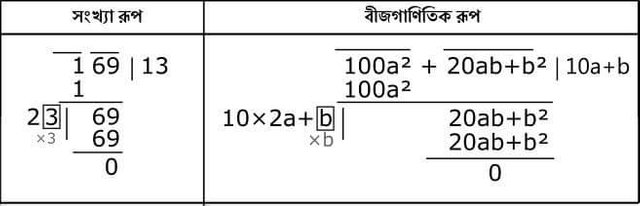

It is not difficult to understand the algebraic form. Earlier, our main source was (10a + b) ² = 100a² + 20ab + b². Notice, in our example a = 1 and b = 3 Now look at the 10 × 2a + b ratios 2a, it is understood to be twice as much as what is in the square root. Keep a place next to 10 times. Then there is a b to be found, so that (10 × 2a + b) × b = 20ab + b² is found. And the group we used to do was grouped in two doors, it looked like 100a². Because of 100 times there will be two vacuums, that means there will be two houses.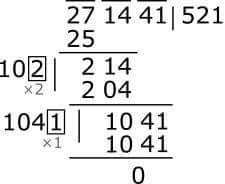

One thing, the square root here was 13, two figures. So a, b is easy to understand. But if it is more substantial than that? Let's assume square root 521 which is three digit, meaning the original number is 271441. Then what will be a, b? Then we can think of 521 as 10 × 52 + 1 size. Meaning, a = 52, b = 1 can be considered.
Seeing in the next picture, you can imagine. I thought for 2714 at the beginning. There, we've got a = 5 and b = 2. The result is 5 × 2 = 10 left side. Then, in the empty room, 2 with 102 × 2 = 204, the result is 10. Notice, if this 10 were not remaining, if the number was 2714 and not 2704, we would actually get a square of 52. But we have 10, then the next group has dropped 41. This time we had to think a = 52 and b = 1; Then, on the left side, 52 is doubled to 104, then in the empty room, 1 nilei is matched with 1041 × 1 = 1041.

This matter can be understood more clearly if it is considered directly to the class of 52. In that case, a = 52, a² = 2704, 2ab = 104, b² = 1.

Cubic rules:
We want to learn from the past. Since the square (10a + b) ² we thought we would think about cube (10a + b) ³. We need to look carefully at this amount
(10a + b) ³ = 1000a³ + 300a²b + 30ab² + b³
From here we will try to understand, the algebraic form of solid molecule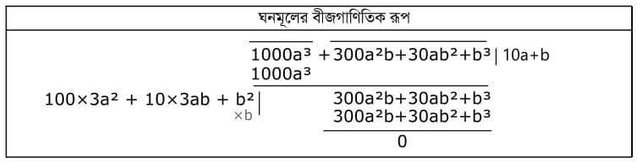

Please note that the difference with the rule of the square root rules. It can be said from 1000aে, we will have to make groups in three to three. In the first group, there is a number of densities, it should be seen, then the next group with the difference and the next group has to be reduced. Then the real event is then. First, I took double that which was in the square root area, then I kept a blank room. In this case, the area of ​​the concentration will have to take three times its square (3a²). Then the two rooms are to be empty, since there is 100 times 3a². There is 10 times 3ab, so it will be in the house of Dasak. And in the unit's house there will be b². But how much will that be? One such digit number b has to be found, so that in the middle of the house 3ab and b² in the last cell, the whole number can be found, with the number of times b gives it inside and then goes into the result. I know, it just can not be understood by reading the text.
With an example, hopefully it will be clear. Once the example is understood, read the above text another time. Then it will be easy to understand.
Example: What is the concentration of the number 12167?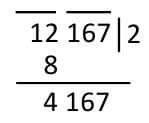

1.Create groups with three to three cells starting from right to right. Each mark with a mark on each group.
2.In the first group, I see the maximum number of times in it. Here goes in 12 to 2³ = 8. I write 2 in the place of solid. At the bottom of the 12 we have 2 solid 8 subtracting is 4. Then the next group was named 167.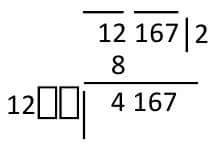

3.On the left hand side of the triangle, I gave a stain like a division. There is a 'three times the square' (3a²) of what is in the concentration area and place two chamber spaces beside it. There was a place of concentration 2 Its square 4, it's three times 12 So I wrote 12 and put two places with two boxes.
4.The most important (and trouble) part of this time. Those empty spaces will have to find out what they will sit on. If you place 3ab in the middle room and put b² in the last cell, then the whole number gets to be filled with the number of times it goes into b in the input field. Examples can be understood well. I am showing the values ​​of b 1, 2 and 3 of b, how to calculate the empty cells. Take care here a = 2 (which is in the concentration place)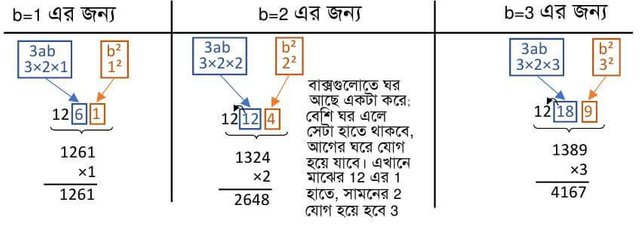

Wow, we can see that the value for 3 is matching with 4167. If we put 3 in the solid surface of 2, we'll get the whole volume of the solid. For example, it is 23 that is our concentration. The whole process can be summarized in the picture below.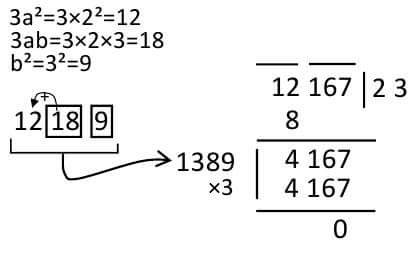

Note that 3ab = 18 will sit in 8 boxes and 1 will be in the hand. It will be 13 in the next 12. If there were any two-digit numbers in the unit's house, there would have been the same thing. For example, b = 4 would have been 16. Then I put 6 in the unit house and sent one to the previous house to the house of the decade and add it to the house.
Another thing should be said here.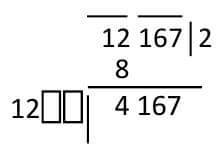

Do we have to go through the value of b every time? Until it matches? The answer is - no! If you think with a little bit of intelligence. Notice, after typing 2 in the solid base we wrote down the left side 12, then we left two rooms empty. That meant it was 1200. And our downfall was 4167, just guess 4100. Without thinking about zero (00) you can think. How many times with 12, a little less than 41 will be available? 12 × 2 = 24, 12 × 3 = 36, 12 × 4 = 48, that means that 4 will be greater. May be 3. For this, you can start trying the value of b directly with 3. After all calculations, if the last product was more than the truncator, then we tried it with the previous number 3.
This is the rule. But I will show a few more examples. Then those who are still skeptical will benefit them.
Example: Determine the concentration of 74088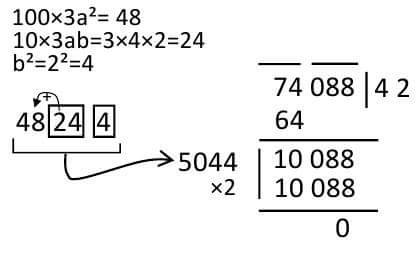

Example: Determine the concentration of 17576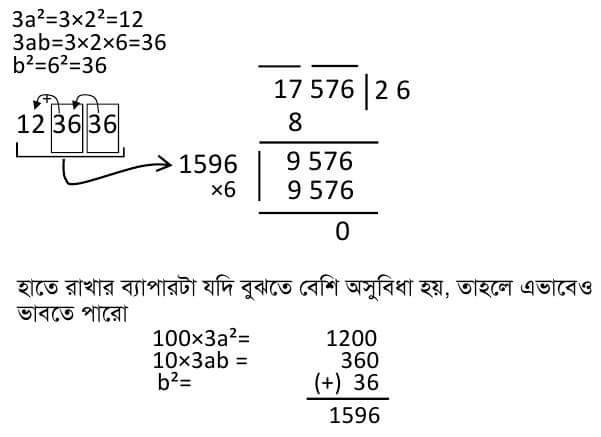

Example: Determine the concentration of 1906624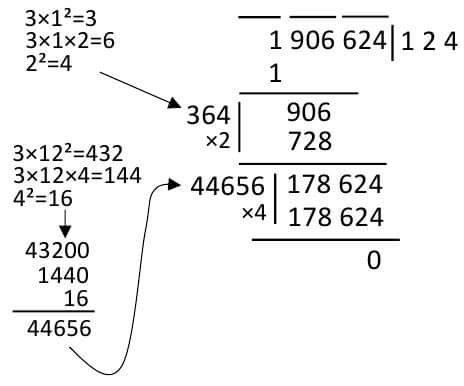

Example: Determine the concentration of 1906.624
If there is a decimal, two things should be considered extra: group how to do and where the decimal places sit. The group has to think separately before and after the decimal. The decimal before the decimal and the number of the three numbers from the last three to the group. The decimal parts should be grouped from three to the right, from the decimal to the right, if necessary, fill it with zero. For example 12345.6 group group will be written 012 345. 600. And where the decimal will sit, it is just like the common denominator. Whenever there is a group after the decimal from above, sit at a decimal place in the concentration area. See below, which has not been 624, has placed a decimal at 12 after the above. Here's an example with a decimal. (This is actually the previous example, I just put a decimal at a time).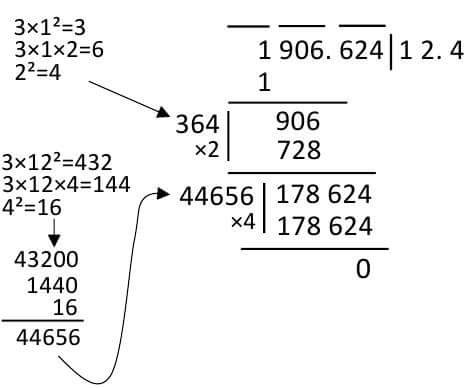

Last talk: Congratulations, those who have come to patience with you so far. If you really understand, then you just have to get an idea of how to find the nth root, not the solid values, (n here is the greater integer than 1).