Forms of Complex Numbers
To start, let me give a brief introduction of complex numbers. A |complex number| is a number of the form a + bi, where a and b are real numbers and i is the imaginary unit, satisfying i^2 = -1.
Example:
-3.5+2i
|Notation:|
Some authors write a+ib instead of a+bi, particularly when b is radical. In some disciplines, in particular electromagnetism and electrical engineering j is used instead of i, since i is frequently used for electric current. In these case compx numbers are written as a+bj or a+jb.
Below are the forms of complex numbers:
1 | Rectangular Form |
Rectangular form, on the other hand, is where a complex number is denoted by its respective horizontal and vertical components.
(https://www.allaboutcircuits.com/textbook/alternating-current/chpt-2/polar-rectangular-notation/)
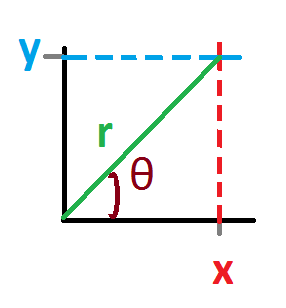
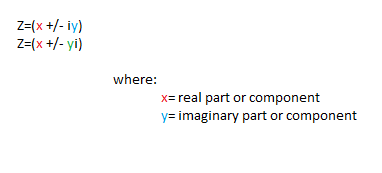
Example: 5-2j
2 | Polar Form |
Polar form is where a complex number is denoted by the length (otherwise known as the magnitude, absolute value, or modulus) and the angle of its vector (usually denoted by an angle symbol that looks like this: ∠).
(https://www.allaboutcircuits.com/textbook/alternating-current/chpt-2/polar-rectangular-notation/)
Example: 5-2j = 5.49∠-21.80°
3 | Trigonometric |
Example: 5-2j = 5.49cjs(-21.80)°
4 | Exponential form |
Example: 5-2j = 5.49e^(-0.381)
There are also simple ways to convert complex number forms to any of those forms, I will include it on my next post on complex numbers.
Reference:
Advanced Engineering Mathematics ( compilation and workbook) from University of Cebu L-M
(author of the book is not stated on it)


