To keep my algorithm skill sharp so I don’t lose my touch, I’ve decided to solve a few algorithm problems every day (hopefully~) and track my progress here.
Today’s focus is on problems related to summing elements.

Two Sum

The difference of "Two Sum" from "Three Sum": "Three Sum" is sorted and uses the two-pointer technique.
Additionally, this problem requires using a map instead of a set because the problem asks for returning indices rather than values. Moreover, we are finding the corresponding index through the "value," so it's map<value, index>.

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> heap;
        for(int i = 0; i < nums.size(); ++i){
            int r = target - nums[i];
            if(heap.count(r)) return {heap[r], i};
            heap[nums[i]] = i;
        }
        return {};
    }
};

Three Sum

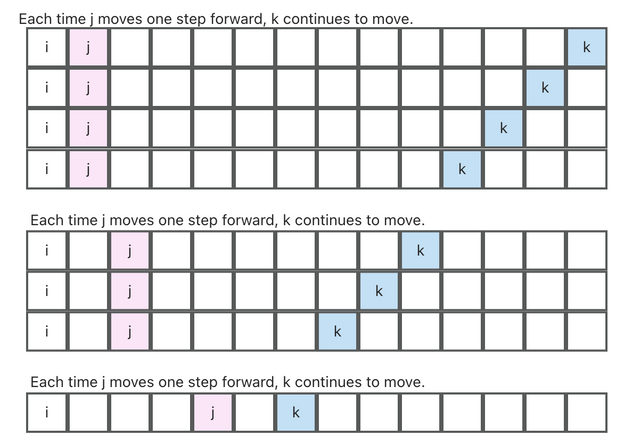
Sorting + Two Pointers

1. Enumerate each number nums[i] as a fixed value.
   • In the sorted array, use two pointers j (starting from i + 1) and k (starting from n - 1) moving towards each other from both ends.
   • Find all valid triplets where nums[i] + nums[j] + nums[k] == 0.
2. During the search for valid triplets, let sum = nums[i] + nums[j] + nums[k]:
   • If sum > 0, move k to the left to decrease the sum.
   • If sum < 0, move j to the right to increase the sum.
   • If sum == 0, a valid triplet (nums[i], nums[j], nums[k]) is found and added to the result ans.
3. Duplicate Handling:
   • When fixing nums[i], ensure j starts from i + 1.
   • If nums[i] == nums[i - 1], skip the current i (as it would yield duplicate triplets) and continue to the next iteration.
   • After finding a valid triplet (sum == 0), skip duplicate values for nums[j] and nums[k] to avoid redundant entries.
     

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> res;
        int n = nums.size(); if(n < 3) return res;
        sort(nums.begin(), nums.end()); // Don't forget: the prerequisite for the two-pointer technique is a sorted array.
        for (int i = 0; i < n; i ++ ) {
            if (i && nums[i] == nums[i - 1]) continue; //cannot be omitted, this is for deduplication. Semantics: i has already moved one step, and if it is the same as the previous nums[i-1], skip to the next, i.e., nums[i+1]
            for (int j = i + 1, k = n - 1; j < k; j ++ ) { // Once i is fixed, proceed with the two-pointer algorithm for j and k.
            // Common mistake: for (int j = i + 1; j < k; j ++ ) k should be initialized in the for-loop initialization, meaning inside for(), j and k always move closer.
                if (j > i + 1 && nums[j] == nums[j - 1]) continue; //cannot be omitted, this is for deduplication. Semantics: j has already moved one step, and if it is the same as the previous nums[j-1], skip to the next, i.e., nums[j+1]
                // Common mistake; int k = n - 1; same as line11, inside for(), j and k always move closer.
                while (j < k && nums[i] + nums[j] + nums[k] > 0) k -- ;  
                    // The reason while() does not check for sum < 0 is because if it is < 0, j++ is handled by the for(j++) in line8.
                if (j < k && nums[i] + nums[j] + nums[k] == 0) {  // Exiting while might be due to j>=k, so ensure j<k. If j==k, it might seem like two zeros (nums[j] == nums[k] == 0), but there is actually only one zero.
                    res.push_back({nums[i], nums[j], nums[k]});
                }
            }
        }
        return res;
    }
};