안녕하세요. ICOREPORT에 @sanghyun 입니다.

비트코인에는 여러 방법의 암호화가 사용됩니다. 그 중에서 키 값들을 암호화 시키는 방법인 타원 곡선 암호화에 대해 글을 써보도록 하겠습니다.

본 자료는 1부,2부로 나뉘어져 있으며 1부는 타원 곡선 암호화를 배우기전 워밍업 정도로 생각하시면 될것같습니다. 2부는 빠른 시일 내로 타원 곡선 암호화에 대해 정리해보도록 하겠습니다.

본론에 나가기에 앞서, 이 글은 블록체인에 관한 국내 자료가 매우 부족하다고 생각하여 해외 자료중 잘 정리된 글을 번역한 것임을 알려드립니다. (원서링크 : https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/ )

---

타원 곡선 암호화(Elliptic Curve Cryptography)는 오늘날 가장 널리 사용되고 있지만 이해하기 어려운 유형의 암호화 기술 중 하나입니다. CloudFlare에서는 ECC를 광범위하게 사용하여 고객의 HTTPS 연결에서 데이터센터간에 데이터를 전달하는 방법까지 모든 것을 보호합니다.

근본적으로 모든 보안 시스템의 기술을 이해하기 위해서는 보안 시스템을 이해하는 것이 중요하다고 생각합니다. 사용자들과 공유하기 위해 이해하기 쉽고 좋은 ECC 입문서를 찾아 보았습니다. 그러나 아무것도 발견하지 못한 채, 스스로 작성하기로 결정했습니다. 그리고 내용들은 다음과 같습니다.

공개 키(Public key) 암호의 시작

암호학의 역사는 고전 시대와 현대 시대의 두 시대로 나눌 수 있습니다. 1977년에 발생한 둘 사이의 전환점은 RSA 알고리즘과 Diffie-Hellman 키 교환 알고리즘이 도입 된 때였습니다. 이러한 새로운 알고리즘은 보안이 숫자 이론을 기반으로하는 최초의 실행 가능한 암호화 체계로 등장했기 때문에 혁명적이었습니다. 그것은 공유된 비밀 (shared secret) 없이 두 당사자 간의 안전한 통신을 가능하게 해주었습니다.

암호화는 전 세계의 비밀 코드북(codebook)을 안전하게 운반하는것에서부터 키 교환내에 누군가가 청취(listening)하는 걱정 없이 두 당사자 간의 안전한 통신을 보장 할 수있게 해주었습니다.

최신 암호화는 데이터를 암호화하는데 사용하는 키를 공개 할 수 있고 데이터를 해독하는데 사용하는 키는 비공개로 유지할 수 있다는 아이디어를 기반으로 합니다. 이와 같이, 이러한 시스템은 공개 키 암호화 시스템으로 알려져 있습니다. 이 시스템 중 가장 널리 사용된 RSA는 Ron Rivest, Adi Shamir 및 Leonard Adleman 알고리즘을 처음 공개적으로 묘사 한 세 사람의 머리 글자를 따서 명명했습니다.

공개 키 암호화 시스템이 작동하려면 한 뱡항으로는 처리(do)하기 쉽지만 되돌리기(undo)는 어려운 알고리즘이 필요합니다. RSA의 경우, 쉬운 알고리즘은 두 개의 소수를 곱합니다. 만약 곱셈이 쉬운 알고리즘인 경우, 어려운 쌍(pair) 알고리즘은 곱셈의 결과를 두 개의 구성 요소 소수로 분해합니다. 이렇게 한 방향으로는 쉽고 반대 방향으로 처리하기 어려운 특징을 가진 알고리즘들은 트랩도어 함수(Trapdoor Functions)라고 알려져 있습니다. 좋은 트랩도어 함수를 찾는 것은 안전한 공개키 암호화 시스템을 만드는데 중요합니다. 간단하게, 트랩도어 함수에서 한 방향으로 간다음 그 지점에서 다른 방향으로 가는 어려움의 gap이 클수록 암호화 기반 시스템이 더 안전하다고 볼 수 있습니다.

A toy RSA algorithm

RSA 알고리즘은 대중적이고 가장 잘 이해 된 공개 키 암호 시스템 입니다. 이 시스템에서 곱셈은 빠르고 분해는 느립니다. 다음은 RSA 시스템의 작은 모습과 작동 원리를 간략하게 설명합니다.

일반적으로 공개 키 암호화 시스템에는 공개 키와 개인 키의 두 가지 구성 요소가 있습니다. 암호화는 메시지를 가져와서 수학 연산을 적용하여 임의의 숫자를 얻습니다. 암호 해독은 무작위로 보이는 번호를 취하여 원래 번호로 돌아가기 위해 다른 작업을 적용합니다. 공개 키를 사용한 암호화 데이터는 개인 키를 사용하여 암호를 해독함으로써 다시 되돌릴 수 있습니다.

컴퓨터는 임의로 선택된 큰 수(number)들을 잘 처리하지 못합니다. 그래서 최댓값을 설정하여 처리중인 숫자들이 너무 커지지 않도록 만들고 오직 최댓값보다 작은 숫자들만 다루게 하도록 해야 합니다. 숫자들을 아날로그 시계위에 숫자들처럼 다룰 수 있습니다. 최댓값 보다 더 큰 숫자를 만드는 계산은 유효 범위내에 다른 숫자로 랩핑(wrapping) 됩니다.

RSA에서 이 최댓값은 두 개의 무작위 소수를 곱하여 구합니다. 공개 키와 비공개 키는 0보다 크고 최댓값보다 작은 두개의 특수하게 선택된 숫자이고 각각 pub와 priv으로 부릅니다. 한 숫자를 암호화하려면 그 숫자를 pub 횟수 만큼 곱해줍니다. 곱해준 값이 최댓값을 지나치면 줄바꿈(wrap around) 해주어야 합니다. 메시지를 해독하기 위해서 그것을 priv 횟수 만큼 곱해주면 원래의 숫자로 돌아오게 됩니다. 믿기 힘들겠지만 이 과정은 실제로 작동합니다. (이해하기 쉽게하기 위해, 좀 있다 아래에서 예시를 보도록 하겠습니다.)

RSA 키 쌍을 생성하려면 먼저 두 개의 소수를 무작위로 선택해서 최댓값을 구해야 합니다. 공개 키 pub가 될 숫자를 고릅니다. 두 개의 소수 값을 아는 한, 공개 키로부터 대응하는 개인 키인 priv를 계산할 수 있습니다.

이것은 RSA를 깨는 것과 관련된 인수 분해 방법입니다. 최댓값을 구성 요소 소수로 분해하는것은 공개 키로부터 누군가의 개인 키를 계산할 수 있게 해주고 비공개 메시지를 해독할 수 있게 해줍니다.

좀 더 구체적으로 설명해보겠습니다. 소수 13과 7을 사용하면 최댓값은 91 입니다. 공개 키를 5로 설정해 봅시다. 7과 13을 알고 있다는 사실을 이용하여 91의 요소를 적용하고 확장된 유클리드 알고리즘을 사용하면 개인 키가 29라는 것을 알 수 있습니다. 이러한 매개변수들은 완전한 RSA 시스템을 정의합니다. 당신이 숫자를 가져와서 그것을 5 번 곱하면 그것은 암호화되고, 그 숫자를 받아서 29번 곱하면 원래의 숫자를 되찾을 수 있습니다.

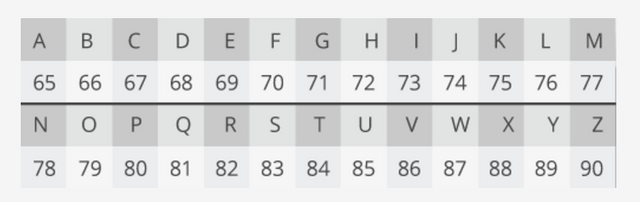
이러한 values들을 사용하여 "CLOUD" 메시지를 암호화 해보도록 하겠습니다. 메시지를 수학적으로 표현하기 위해서는 문자를 숫자로 변환해야 합니다. 라틴 알파벳의 일반적인 표현은 UTF-8입니다. 각 문자는 숫자에 해당합니다.

여기 인코딩에서 CLOUD는 67,76,79,85,68 입니다. 이 숫자들은 모두 최대값인 91보다 작으므로 개별적으로 암호화 할 수 있습니다. 첫글자부터 보도록 하겠습니다.

암호화된 값을 얻기 위해 숫자를 5번 곱해보겠습니다.

67 × 67 = 4489 = 30 
4489는 최댓값보다 크기 줄바꿈을 해야합니다. 우리는 91로 나누고 나머지를 취합니다.
4489 = 91 × 41 + 30
30 × 67 = 2010 = 8
8 × 67 = 536 = 81
81 × 67 = 5427 = 58
즉, 67의 암호화 된 버전은 58입니다.
각 문자에 대한 프로세스를 반복하면 암호화 된 메시지 CLOUD가됩니다.
58, 20, 53, 50, 87
이 스크램블 된 메시지의 암호를 해독하기 위해 각 번호를 가져 와서 29 번을 곱합니다.
58 × 58 = 3364 = 88 (숫자가 최대 값보다 클 때 줄바꿈을 합니다.)
88 × 58 = 5104 = 8
...
9 × 58 = 522 = 67

어떻습니까? 다시 67로 돌아왔습니다. 이런식으로 나머지 숫자들과 함께 작동하여 원본 메시지를 만들어냅니다.

Not a perfect Trapdoor

RSA와 Diffie-Hellman은 강력한 보안 증거를 제시했기 때문에 매우 강력했습니다. 저자는 시스템을 깨는 것이 해결하기 어려운 수학적 문제를 해결하는 것과 동일하다는 것을 증명했습니다. 인수 분해 (Factoring)는 매우 잘 알려진 문제이며 고대부터 연구되어 왔습니다. 이 문제에 관한 어떤 돌파구라도 생긴다면 그것은 커다란 뉴스가 될 것입니다.

즉, 인수 분해(Factoring)은 비트단위에서는 가장 어려운 문제는 아닙니다. Quadratic Sieve 및 General Number Field Sieve와 같은 특수화 된 알고리즘은 소수 분해의 문제를 해결하기 위해 만들어졌으며 비교적 성공적이었습니다. 이러한 알고리즘은 알려진 소수의 쌍을 추측하는 단순한 접근 방식보다 빠르고 계산량이 적습니다.

이러한 인수 분해 알고리즘은 인수 분해되는 숫자의 크기가 커짐에 따라 더 효율적 입니다. 큰 수를 인수 분해하는 난이도와 큰 수를 곱하는 어려움 사이의 갭은 수(즉, 키의 비트 길이)가 커짐에 따라 줄어듭니다.

숫자를 해독하는데 사용할 수 있는 리소스가 늘어남에 따라 키의 크기도 더 빠르게 커질 필요가 있습니다. 이것은 계산 능력이 제한된 모바일이나 저전력의 디바이스에게는 지속 가능한 상황이 아닙니다. 인수분해와 곱셈 사이의 갭은 장기간 지속될 수 없습니다.

이 모든것은 RSA가 암호화의 미래를 위한 이상적인 시스템이 아니라는 것입니다. 이상적인 트랩도어 함수(Trapdoor function)에서는 문제의 숫자와 관련하여 쉬운 방법과 어려운 방법이 동일한 비율로 더 어려워집니다. 그래서 우리는 더 나은 트랩도어를 기반으로하는 공개 키 시스템이 필요한 것입니다.

---

읽어주셔서 감사합니다! 앞으로도 계속 좋은 포스팅으로 뵙겠습니다.

Upvote 하나로 응원 부탁드립니다!