문과 아재도 쉽게하는 R 데이터 분석 – (3) 선형회귀분석 (Linear Regression)
회귀분석
Regression은 회귀분석이라는 이름으로 사회과학, 자연과학 등 학계 전반에 걸쳐 너무나도 자주 쓰이는 분석방식입니다.
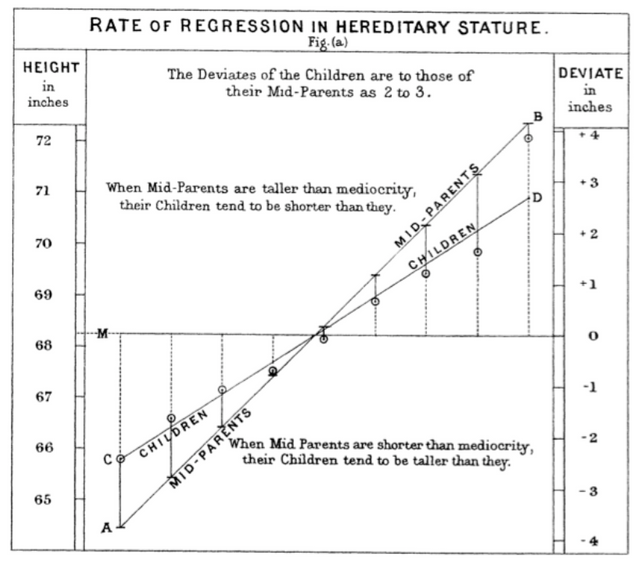
회귀라는 이름은 사실은 그다지 와닫지는 않습니다. 사실은 이름에 대한 유래는 Galton이라는 사람의 실험에서 부터 시작됩니다. 이 실험의 논문 이름은 "Regression towards Mediocrity in Hereditary Stature." 즉, 자식의 키가 부모 두명의 키의 평균으로 회귀(되돌아온다) 한다는 뜻입니다ㅋ. 이 논문에서 자식의 키 분포 그래프에 보조선을 하나 쭉 그어놓은것도 있구요.
그렇게 어떻게 어떻게 하다가 이렇게 각 산점도에 이를 설명할수 있는 선을 그려보기도 하고 모델을 만들어 예측하고 분석하는 방법이 regression analysis라는 이름으로 좀더 의미가 변형 확장되어 전해져왔습니다. 딱히 수축하는 현상하고는 관련이 없습니다.
즉 회귀분석은, 관찰된 변수들에 대해 이들 사이의 모델을 계산하고 적합도를 측정해 내는 분석 방법입니다.
또한 위의 표에서는 자식의 키의 분포에 선을 그어놓고 이에대한 관계에 대해 하나의 선으로 설명해주고 있는데, 지금 이 선은 직선모양을 띄기 때문에, 선형회귀(Linear Regression)라고 불리며 직선이 아닌 형태는 비선형회귀입니다.
Galton 의 연구자료로 돌아가기
회귀분석이 처음나온 시절로 돌아가 Galton처럼 한번 분석을 해봅시다.
install.packages("UsingR")
library(UsingR)
data(galton)
str(galton)
'data.frame': 928 obs. of 2 variables:
$ child : num 61.7 61.7 61.7 61.7 61.7 62.2 62.2 62.2 62.2 62.2 ...
$ parent: num 70.5 68.5 65.5 64.5 64 67.5 67.5 67.5 66.5 66.5 ...
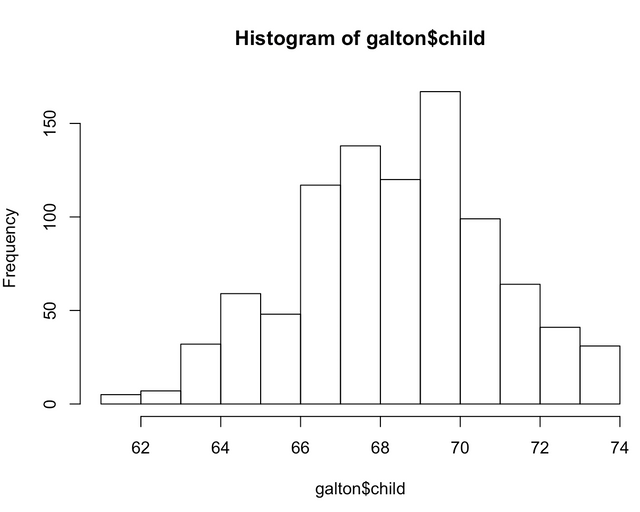
그리고, 데이터들이 제대로 박혀있는지 확인을 해볼수 있습니다.
hist(galton$child)
그리고 여기에 꼭 들어맞는 선형회귀식을 도출해볼수 있습니다.
lm(child~parent,data=galton)
Call:
lm(formula = child ~ parent, data = galton)
Coefficients:
(Intercept) parent
23.9415 0.6463
너무나도 쉽게, 자식의키 = 0.65 * 부모의 키 + 23.94 라는 식이 도출되었습니다.
coefficients 는 계수로써, y=ax+b 라는 식에서 a와 b를 뜻합니다.
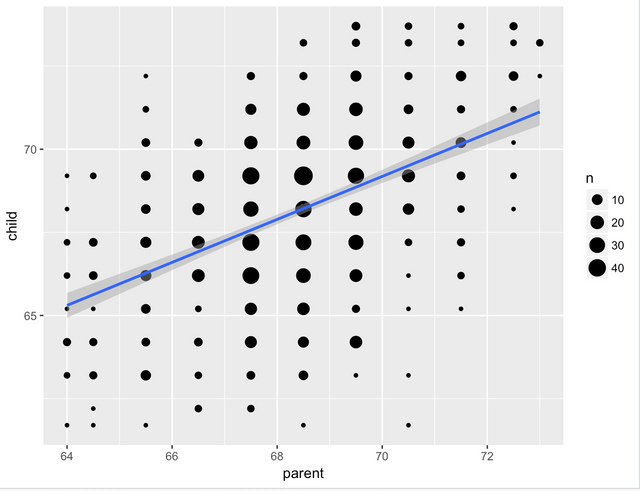
이 모델을 좀더 한눈에 알아볼수있도록 좀더 예쁘게 그래프를 그려볼수도 있습니다.
ggplot(data=galton,aes(x=parent,y=child))+geom_count()+geom_smooth(method="lm")
결론적으로, 자식의 키는 부모의 키와 상관관계가 있되, 부모의 키를 100% 따라가는것은 아닌것로 결론을 내볼수 있습니다. 결국 자식의 키가 부모의 키만큼은 아니고, 그보다 적은 수준으로 평균화되는 현상으로 해석할수도 있겠습니다.
다만, 뭔가 썰렁하기는 합니다. 아마 저 계수들을 얼마나 믿을 수 있는지 어떻게 알수 있을까요? lm으로 나온 변수를 다시 summary를 하면 됩니다.
model <- lm(child~parent,data=galton)
summary(model)
Call:
lm(formula = child ~ parent, data = galton)
Residuals:
Min 1Q Median 3Q Max
-7.8050 -1.3661 0.0487 1.6339 5.9264
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 23.94153 2.81088 8.517 <2e-16 ***
parent 0.64629 0.04114 15.711 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.239 on 926 degrees of freedom
Multiple R-squared: 0.2105, Adjusted R-squared: 0.2096
F-statistic: 246.8 on 1 and 926 DF, p-value: < 2.2e-16
위의 값들은 적당한 p-value와 몇가지의 검증가능한 값들을 제시해줍니다. 일단, 모델의 설명력을 나타내는 R제곱, 즉 결정계수는 0.2로 설명력이 떨어집니다. 모델로는 변화량의 20% 밖에 설명을 하지 못하기는 합니다. 보조선에서 퍼진 형태일수록 결정계수가 낮습니다.
다만 수정결정계수는 뭐하는 정보일까요? 사실 설명하는 변수가 많으면 결정계수가 올라가는것은 당연한 현상이기 때문에 이를 보정해주기위한 값입니다. 좀더 믿을만 하겠죠? 다만 보통의 경우에서는 두 결정계수가 차이가 크게 나지는 않으므로, 결정계수가 0.5 이상이면 충분히 설명력 있는 모델이라 할수 있습니다.
유의성을 살펴보는 p-value값들은 모두 2e-16으로 관습적으로 사용하는 0.05보다 낮은 값입니다. parent계수는 미슐랭 별처럼 별 ***로써 믿을만 합니다.
p-value는 유의수준을 나타내는 값으로, 우연히 규칙성있게 나올 확률이 0.00000....2 퍼센트를 기록하고 있다는 것입니다.엄청나게 낮은 값이죠? 다만 이 값이 0.05 이상이면 해당변수를 사용하거나 해당 모델을 사용하는것을 다시 고려해봐야합니다. 대충 어쩌다가 나온 결과를 진리인양 말하는 결과가 될 수도 있기 때문입니다.
F통계량은 그룹간 분산의 차이가 있는지에 대한 결과를 보고싶을때 쓰는데, 그렇다면 모델은 하난데 어떤 것과 비교를 하길래 F통계량을 쓰는걸까요?
바로,
- 예측치는 그냥 지금까지 나온 숫자의 평균과 같다라는 가정,
- 열심히 컴퓨터를 돌려 만든 회귀식
두개가 실제로 다른가를 보기위한 분산을 구해서 비교해보는겁니다. 마찬가지로 두개가 우연히 나올 확률이 굉장히 높으면 회귀식은 쓸데가 없는것이고, 낮으면 열심히 돌려만든 회귀식이 타당하다는데 한표를 던질수있습니다.
머리가 아프다면, p-value가 충분하게 낮은지만 체크하시면 됩니다. 보통 힘을 잘쓰는 타당한 변수라면 0.05보다는 훨씬 낮은 값을 보이게 됩니다.
예측하기
모델이 나왔으니, 이걸로 간단하게 예측해볼수 있습니다.
parents <- data.frame(parent = c(60,65,70))
predict(model, parents)
1 2 3
62.71897 65.95042 69.18187
사실은 y=ax와 같은 방정식에 값만 대입하는 행위와 다를바가 없는데, 어쨌든 값을 예측하는것을 확인할수 있습니다.
다중회귀
지금 자식의 키를 예측하는 변수는 부모의 키 단 하나이나, 이가 여러개가 될수도 있습니다.
예를들어, 아이의 수명을 예측하는 모델을 만드는데 있어 다음과 같이 가능한 모든 변수를 넣어서 계산할 수 있습니다.
data(swiss)
model <- lm(formula = Infant.Mortality ~ ., data = swiss)
summary(model)
Residuals:
Min 1Q Median 3Q Max
-8.2512 -1.2860 0.1821 1.6914 6.0937
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.667e+00 5.435e+00 1.595 0.11850
Fertility 1.510e-01 5.351e-02 2.822 0.00734 **
Agriculture -1.175e-02 2.812e-02 -0.418 0.67827
Examination 3.695e-02 9.607e-02 0.385 0.70250
Education 6.099e-02 8.484e-02 0.719 0.47631
Catholic 6.711e-05 1.454e-02 0.005 0.99634
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.683 on 41 degrees of freedom
Multiple R-squared: 0.2439, Adjusted R-squared: 0.1517
F-statistic: 2.645 on 5 and 41 DF, p-value: 0.03665
다만, 몇가지 변수는 p-value가 너무 높습니다. 이럴경우에 어떤 변수를 택해야 하는가의 문제가 있을수 있습니다. 이럴경우에는 변수를 하나씩 추가해보거나 하나씩 제거해보고 모델의 설명력을 측정하는 방식을 쓰면 편합니다. 이를 자동으로 해주는 함수는 step() 이 있습니다.
smodel <- step(model)
summary(smodel)
Residuals:
Min 1Q Median 3Q Max
-7.6927 -1.4049 0.2218 1.7751 6.1685
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.63758 3.33524 2.590 0.012973 *
Fertility 0.14615 0.04125 3.543 0.000951 ***
Education 0.09595 0.05359 1.790 0.080273 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.614 on 44 degrees of freedom
Multiple R-squared: 0.2296, Adjusted R-squared: 0.1946
F-statistic: 6.558 on 2 and 44 DF, p-value: 0.003215
결국 쓰잘데기없는 변수 빼고 중요한 변수 두개가 선택된것을 볼수있습니다. 사실 이렇게 변수를 줄이는것도 좋지만, 예를들어 1,2,3..12월까지 나열되어있는 경우 이를 적당히 성수기 / 비성수기로 바꾸거나 변수의 형태를 좀 단순화 시키는것도 예측력을 높이는데 도움이 됩니다.
사실 훈련과정에서는 무조건 변수를 다 때려박는게 결정계수등이 높게 나옵니다. 다만, 이를 가지고 훈련에 이용되지 않은 데이터를 예측하기 위해서 모델은 너무 복잡하기만 하다면 과최적화 (Overfitting)이 되어있을 확률이 높습니다.
적당한 변수를 골라내는일과 단순화시키는 일은 중요합니다.
성별과 같이 명목형 변수가 숨어있으면 어떻게 합니까?
명목형 변수가 독립변수에 숨어들어있으면, 수치형 데이터로 바꿔주기가 뭐합니다. 예를들어, 자동차 가격에 대한 예측을 할때 색깔에 따라 가격이 변경될수 있다고 한다면 빨강, 파랑, 녹색등은 어떻게 구분할것인가요? 단순히 1,2,3의 수치로 변환한다면 수치 자체에 큰 의미가 없는데도 녹색은 빨강의 세배라는 의미를 가지게 될수도 있습니다.
굳이 모델을 분리할필요가 없으면 이러한 경우, 원핫인코딩이 필요합니다. 하지만 R은 편리하게도 (여타 다른 패키지와는 다르게) factor가 설명변수에 숨어있으면 알아서 더미변수를 만들어서 해석합니다. 즉, 인종에대해 황인,흑인,백인이 있다면 제일 기준이 되거나 숫자가 많은 데이터를 제외하고 RaceBlack, RaceWhite 변수를 하나씩 만들어서 이에대해 0과 1로 판단을 하게 됩니다.
이는 실제로, 회귀 기울기를 바꾸지는 않고 절편만을 바꾸어 평행하게 움직이는 역할만을 해줍니다.
물론 처음에는 인종별로 모델을 쪼개는 방안도 생각해볼수있을 것입니다. 다만, 모델을 쪼개는 순간 훈련할수 있는 데이터는 확 줄어들기 때문에 전체적인 경향이 같다면 절편만을 이동하게 해주는 원핫인코딩 방식이 훨씬 나은 방법입니다.
회귀분석의 표준 가정
회귀분석은 사실, 어느정도의 데이터에 대한 가정이 존재합니다. 이는 다음과 같습니다.
1.오차항(residuals)은 모든 독립변수 값에 대하여 동일한 분산을 갖는다.
2.오차항의 평균(기대값)은 0이다.
3.수집된 데이터의 확률 분포는 정규분포를 이루고 있다.
4.독립변수 상호간에는 상관관계가 없어야 한다.
5.시간에 따라 수집한 데이터들은 잡음의 영향을 받지 않아야 한다.
이게 무슨 소리냐 하면, 각각의 데이터들이 정규분포로 잘 분포되어있어야 하며 뭔가 쏠린게 없이 잘 되어있어야 한다는 겁니다.
잔차(Resudual)분석
잔차분석은 뭔가 모델에서 설명하고 남은 잡것(?)들을 가지고 분석을 하는것인데, 사실 뒷처리하는 느낌이 강하지만 사실은 회귀분석에서 제일 중요한 검증작업중에 하나입니다.
예를들어 키를 예측하는 모델인 키cm = 2 * 몸무게kg 라는 식을 도출해내었다고 합시다. 이 모델은 너무나도 단순해서 잘 맞지 않지만 그럴듯합니다. 90kg의 사람은 대충 180cm가 결과로 나올것이기 때문이죠. 하지만 50kg을 넣는다면요?
여기서 잔차란 2 * 몸무게라는 방정식으로 몸무게 50kg 를 집어넣어 나온 키의 예측치 100cm과 실제 관측된 키인 160cm과의 차이인 60을 뜻합니다. 이 모델은 잔차가 규칙을 띄고있을 가능성이 있습니다. 항상 뭔가 나머지가 많이 남을 것 같은 느낌이죠? 만약 제대로 세워진 모델이라면 이 잔차에는 특별한 규칙없이 나머지가 중심값을 중심으로 퍼져있어야 합니다. 제대로 만들지 않았다면 잔차는 규칙을 띄게 되며 이는 그래프를 그리면 확인하기가 편합니다. 한번 해볼까요?
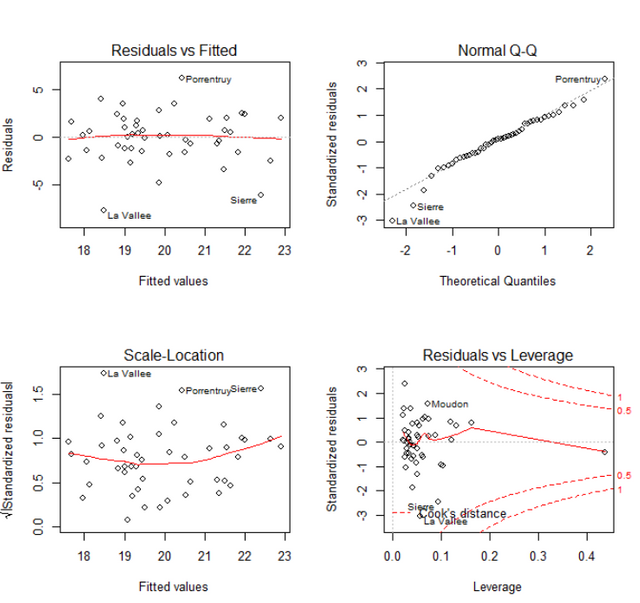
plot(smodel)
보는 방법은 정말 간단합니다. 첫째 그래프는 실제 잔차가 어떻게 분포되어있나 호가인하는 부분입니다. 아무 패턴이 발견되지 않으면 잘 모델이 완성되었다고 할수 있겠습니다. 다만, 가끔은 찌부러진 형태가 나타나기도 하는데 이럴때는 모델의 y의 제곱근으로 예측을 하거나 하는방법도 존재합니다.
셋째그래프는 첫째그래프의 제곱근 스케일이라 보통은 하나가 별다른 패턴이 없으면 나머지도 마찬가지입니다.
그리고 둘째그래프에서는 Quantile - Quantile그래프인데, 잔차도 예측값을 중심으로 고르게 퍼져있되, 보통은 정규분포를 따르게 됩니다. 이론상 이 잔차가 분포되어있는 형태는 대각선이며, 그 위에 점들이 대각선 위에 적당히 분포해 있으면 잔차는 잘 정리된것으로 생각할수 있습니다.
잔차분석은 회귀분석에서는 꼭 짚고 넘어가야 하는 부분입니다. 눈을 질끈감아버리고 넘어간다면, 아마 설명력이 떨어지는 아쉬운 모델이 탄생하겠죠?
잘 읽었습니다 :)
도움이 됐어요 ㅎㅎ
감사합니다~
Congratulations @gillime! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!