야구 피칭 시뮬레이션하기 How to simulate baseball pitching
0. 시작하기 전에
이 글은 reference [1]의 홈페이지의 글을 참조해서 작성했습니다.
자동차 바퀴를 해석 했던 저번 글[2]과 마찬가지로 야구공을 던졌을 때 그 궤적이 어떻게 될지 예측/해석하는 문제 역시 동역학의 문제 입니다. 그냥 강체인 동그라미를 던지는 것과 달리 야구공은 실밥이 있기 때문에 공기 저항으로 작용하는 힘이 다소 복잡합니다. 하지만 저자는 몇가지 가정으로 간단하게 해석했습니다.
- 투수가 최초 공을 던진 회전 속도는 날아가면서 변하지 않음.
- 야구공은 강체
- 필드에 별다른 유동이 음슴.
- 투수는 오른손 잡이
1. Free body diagram
역학 문제를 풀 때 흔히들 힘을 찾으라고 합니다. 이 경우에는 야구공에 작용하는 힘을 찾아야한다는 이야기가 됩니다. Free body diagram이란 것은 세상에 야구공만 있다고 봤을 때, 야구공에 작용하는 힘을 표시하는 방법입니다. 이건
역학에서 아주 중요한 도구이기 때문에 교수님들이 학생들에게 화살표 꼽는 놀이를 많이 시킵니다. 이걸 잘하는 사람들이 역학을 잘하거든요(전 잘 못함 ㅎㅎㅎ)
야구공의 자유물체도는 아래와 같습니다, 검은색 화살표가 야구공에 작용하는 힘이에요.
위 그림처럼 공의 방향이 왼쪽으로 날아가고 있을 때, 공이 시계 방향으로 회전한다고 하면, 공에 작용하는 힘은 총 3가지가 있습니다.
- 공의 무게에 의한 중력,
- 공기 중을 날아갈 때 작용하는 공기저항 drag force
- 공기 중에서 회전할 때 작용하는 매그너스 힘 Magnus force
2. May the force be with you
스타워즈에서 쭉 말하듯, 포스가 우리와 함께 합니다.
- 공에 작용하는 중력은 그 유명한 F = mg , 더이상 설명이 必要韓地?
- 공기저항 Fd = f(v) * v * v_i
수식 입력이 좀 어려워서 ... v는 속도 벡터의 크기이고, v_i 는 속도 벡터를 말합니다. 말로 하니 복잡한데, x축에 대한 drag force를 계산하는 방법은 아래 소스처럼 계산합니당.
Fd_x = fv(v) * sqrt(vx[i]**2 + vy[i]**2 + vz[i]**2) * vx[i]
사실 공기저항은 공기의 밀도랑 날아가는 물체의 단면적 등으로 계산하지만 앞서 말했듯 야구공에 작용하는 공기저항은 실밥이랑 평평한 부분이 섞여있어서 많이 복잡해집니다. 그래서 Giordano [3] 라는 분이 제안한 실험식을 사용하여 drag을 계산합니다.
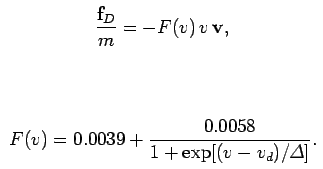
- 매그너스 힘 Fm = B * w X v_i
매그너스 힘은 베르누이 정리에 의해 발생하는 힘 입니다. 가장 간단하게 베르누이 정리를 설명하자면, 에너지 보존 법칙에 의해 유체의 속도가 빨라지면 압력이 줄어들고, 속도가 느려지면 압력이 커지는 현상으로 설명할 수 있습니당.
위 식에서 w X v_i 는 회전 벡터 w와 속도 벡터의 외적 cross product를 말합니다.
또한 위 식의 B 역시 미지수 이지만 Giordano가 제안한 상수B = 4.1*10**-4를 사용합니다.
=>
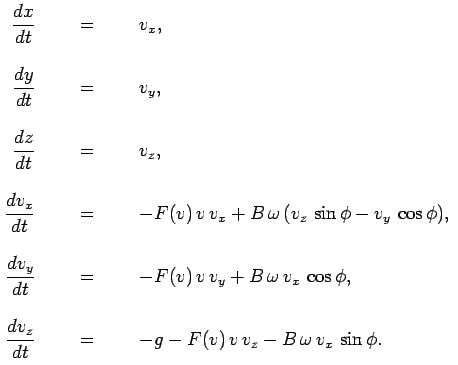
[이거만 풀면 끝! 개쉽다!]
3. 피칭
저는 야구를 잘 몰라서 직구랑 커브볼 정도가 전부 인줄 알았는데 최소 네가지가 있더라구요(너클볼이라는 것도 있었음). 그 중에 익숙한(?) fastball과 curveball을 시뮬레이션 해볼거에요.
[이게 투수들의 기본 스킬??]
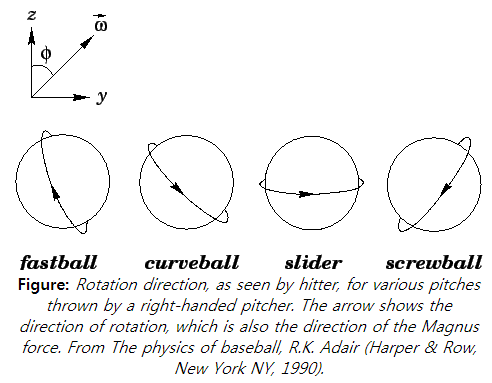
위 그림에서 눈여겨 봐야할 것은 y-z 좌표 입니다. 타자를 기준으로 회전 벡터가 어떻게 정의되는지 보여 줍니다. 회전 벡터는 오른손 법칙으로 정의 됩니다. +y 방향은 타자 기준으로 오른쪽을 말하고, +z는 하늘 방향을 의미합니다.

[손가락이 감기는 방향으로 회전 하는 경우 벡터의 방향은 앰지!]
그리고 저자는 Fastball의 회전 벡터각 Φ는 225º 이고, curveball은 45º 이고, 속도는 각각 95 mph와 85 mph로 가정 합니다. 야구공 던져본 기억이 없어서 직구와 커브볼의 각이 저게 맞는지는 모르겠지만, 저자가 그린 위의 네가지 피칭에서 오른손 법칙에 따라 쥐어보면 앰지의 각이 대강 저렇게 나오는구나... 하고 이해할 수 있습니다.
사실 자유물체도가 나오고, 계산하기 어려운 drag coefficient와 Magnus force의 계수들을 구하는 실험식과 무차원수가 나온 시점에서 어려운 점은 별로 없겠지만, Magnus force 항이 왜 저렇게 나왔는지에 대한 의문이 있다면 그건 좌표계의 정의 때문이거나, 매그너스 힘이 회전 벡터와 속도의 크로스곱으로 구해진다는 사실을 몰랐기 때문일 것 입니다.
4. Simulation
위 시뮬레이션은 간단한 Ordinary Differential Equation 입니다. 식이 여섯개나 있어서 처음 볼땐 동공지진이 생길 수 있지만, 자세히 보면 그냥 각 좌표축에 대한 가속도를 표현한 것 입니다.
가속도에서 속도를 구하는 방법은 이미 한번 다뤘지요. [4]
초기값을 설정하고, iteration을 돌면서 가속도를 계산하면 됩니다. 저자는 4th order Runge-Kutta method를 이용해서 풀었다고 합니다. 상미분 방정식을 푸는 방법 중 하나로 정말 많이 사용한다고 합니다, 전 사실 실전(?)에서 써본 적은 없지만 수치해석을 배울 때 중간고사인지 기말고사에 등장했었던 기억은 납니다.
하지만 귀찮으므로 그냥 예전에 쓰던 방법[4]대로 풀겠습니다.
5. Results
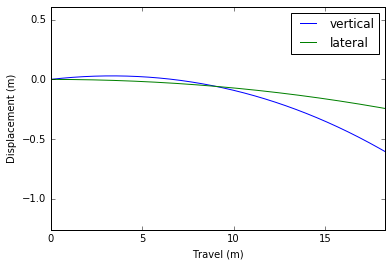
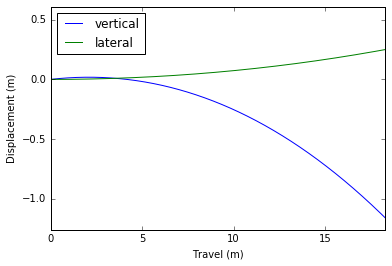
[Fastball(위)과 Curveball(아래)의 궤적]
직구와 커브는 횡방향 운동에서 확연히 차이가 나네요. 낙폭에서도 큰 차이가 나구요. 그래서 커브라고 하는 모양입니다. 신기 ㅋㅋㅋ
[1] http://farside.ph.utexas.edu/teaching/329/lectures/node44.html
[2] https://steemit.com/kr/@emalron/byvbj
[3] Computational physics, N.J. Giordano, (Prentice-Hall, Upper Saddle River NJ, 1997).
[4] https://steemit.com/kr-dev/@emalron/how-to-calculate-velocity-in-game-engine
@_@.. 乃
더 쉽게 써야겠군요 ㅠ.ㅠ
그러고보니 인겜갤러 셨군요! 매번 감탄하고 있습니다. 갠적으로 에말론같은 기획자님하고 일해보고 싶어요 ㅠㅠ
하하;;; 기획이라기엔 아직 갈길이 아주 멀었쬬 ㅠ.ㅠ
흥미로운 주제입니다.
마구마구도 저런 알고리즘을 쓰나요?
저도 궁금해서 검색해봤는데 마케팅 포인트로 그런 이야기가 없는걸 보면 다른 방법으로 한 것 같긴 합니다만 ...
저렇게 식을 풀면 간단하게 파라메터를 바꾸는 것만으로도 여러가지를 쉽게 구현할 수 있는데, 굳이 이상한 방법으로 궤적을 만드는건 더 수고로울 것 같다는 생각도 듭니다.