심시티 개발 0: System dynamics
0. 심시티 개발
Simcity는 Maxis에서 Will Wright가 오래 전에 개발하여 엄청난 히트를 쳤던 도시 경영 게임입니다. 아주 유명하죠, 위키피디아를 보니 1989년에 개발되었다고 합니다. 도시가 망했어요, 시장이 되어 도시를 사렬주세요! 이런 느낌의 도시 경영 게임 입니다. 주거지를 선택하고, 공업지, 상업지를 만들고 여러가지 정책으로 도시를 만들어가는 게임 입니다.
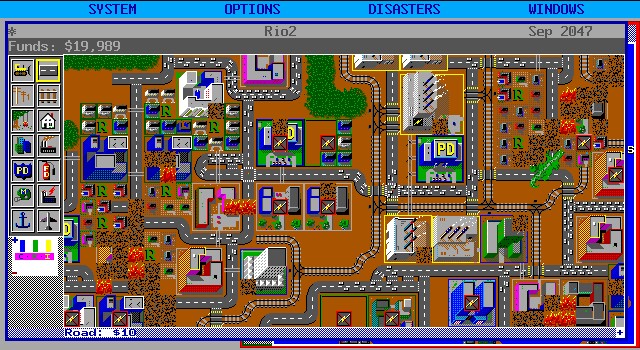
그림 1. 첫 심시티 [1]
위키에도 있지만, 윌 라이트 관련 영상을 살펴보면 Jay Wright Forrester 라는 이름이 등장 합니다. 저도 자세히는 모르겠지만, 이 사람이 도시와 주변 환경의 관계를 정량적으로 해석할 수 있는 방법론을 제안한듯 합니다. 1961년 Industrial dynamics에서 시작해서 urban dynamics, world dynamics 이런 저서들을 출판했거든요. 이 중 urban dynamics가 심시티에 큰 영향을 미친 모양입니다. [2]
1. System dynamics
제이 라이트 포레스터의 system dynamics가 심시티에 준 영향은 아마 각종 요인들이 도시의 인구에, 시민들의 행복도에 어떻게 영향을 주는지 도식적으로 표현하고, 미분 방정식으로 분석할 수 있게 해준 것으로 보입니다.

그림 2. 심시티 매뉴얼에 들어있었다는 City dynamics 차트 [3]
위 차트를 보면 Pollution은 industrial population과 traffic에 +가 찍혀있습니다. 공업단지의 인구와 도시교통이 늘어나면 도시의 오염도가 증가한다는걸 의미하죠. 직관적인 관계입니다. 윌 라이트는 이런 식으로 각 요소 간의 인과관계를 표현하여 유기적인 도시 시스템을 만들었습니다.
이런 인과관계를 그림으로 표현한 Causal loop diagram 을 살펴 보는 것이 심시티 로직을 이해하는데 도움이 될 것 같습니다.
2. Causal loop diagram
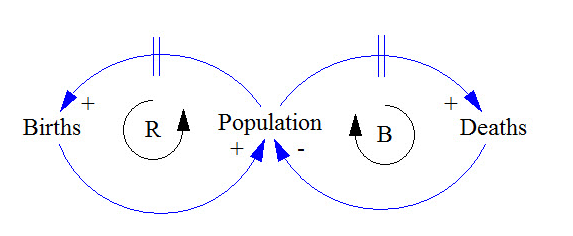
그림 3. 누군가 죽고, 누군가 태어나고 [4]
위 그림이 Causal loop diagram 입니다. 위 다이어그램에서 Births가 Population에 +로 들어가고, Deaths가 -로 들어가는 것은 당연히 누군가 태어나면 인구가 증가하는 것이고, 누군가 죽으면 인구가 감소한다는 이야기겠지요.
여기서 한가지 눈여겨 봐야할 점이 있습니다. Population에서 나온 화살표가 각각 Births와 Deaths를 가르키고 있고, R과 B라고 적힌 것이 있습니다.
이것은 각각 Reinforcing loop와 Balancing loop라고 하여, Positive feedback과 negative feedback을 의미 합니다. 즉, 도시에서 태어나는 아이의 숫자는 그 도시의 인구에 영향을 받는 것이고, 도시에서 사망하는 사람들의 숫자도 도시의 인구에 영향을 받는다는 이야기 입니다.
어떤 일의 결과가 다시 원인에 영향을 미치는 관계를 feedback 이라고 합니다.
3. Feedback
말로 설명하는 것보다 수식으로 보면 더 쉽게 이해가 갑니다. 일단 positive feedback loop 부터 해석해봅시다. 재밌을거에요.
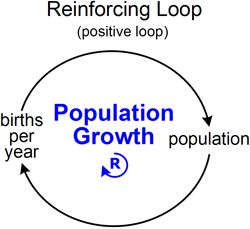
그림 4. 피드백 루프의 Hello, world!
births per year를 B라는 상수라고 하고, 인구를 p 라고 합시다.
매년 증가하는 인구는 현재 인구에서 B의 비율만큼 태어나겠죠? 즉, 인구 1000명일 때 매년 10명씩 새 생명이 태어난다고 하면 B = 10/1000 = 0.01 입니다.
도시의 현재 인구는 p 이므로, 다음 해 도시의 인구는 p + B*p 입니다. 이 관계를 미분식으로 나타내면, 다음과 같습니다.
dp/dt = B*p
흔히들 인구가 exponential하게 증가한다. 라고들 하잖아요? 그 이유는 위 방정식의 해가 p = C1*exp(Bt) 이기 때문입니다. 간단한 적분이니 복습겸 해보면 재밌습니다.
미분식을 컴퓨터로 계산하기 위해선 이산화를 하는게 좋으므로 아래와 같이 계산할 수 있습니다.
p[i+1] = p[i] + dt * (B*p[i])
negative feedback이면 위 식에서 B가 음수가 되는 관계입니다. 그걸 -D 라고 합시다.
그럼 여기서 그림 3의 식은 어떻게 될까요?
dp/dt = B*p - D*p
태어나는 만큼 (Bp) 더하고, 사망한 만큼 (Dp) 빼준 것이 t와 t+1 사이의 변화량이겠지요.
이게 전부는 아니지만 피드백 시스템이, 그리고 causal loop diagram이 미분/적분 형태로 어떻게 해석되는지 이해하는데는 충분한 것 같습니다.
4. Predator-Prey equations
세상 세상 토끼만 잡는 늑대가 40마리 있다고 합시다, 이 늑대들이 등따숩고 배부르게 늙어뒤질려면 토끼가 몇마리여야 할까요?
이런 먹이 사슬 관계를 나타내는 미분 방정식이 있습니다. Predator-Prey equations라고도 하고, Lotka-Volterra equations라고도 합니다.
dx/dt = a*x - b*x*y
dy/dt = c*x*y - d*y
위 식은 아주 가혹한 가정이 있습니다. 모든 토끼들은 자연사 하지 않고, 늑대에게 양념당할 운명이란 것 입니다. 흑흑 ㅠ.ㅠ 넘나 슬픈 것 ㅠ.ㅠ
그래서 늑대(y)의 인구가 0이면 어떤 토끼도 죽지 않습니다(bxy = 0)
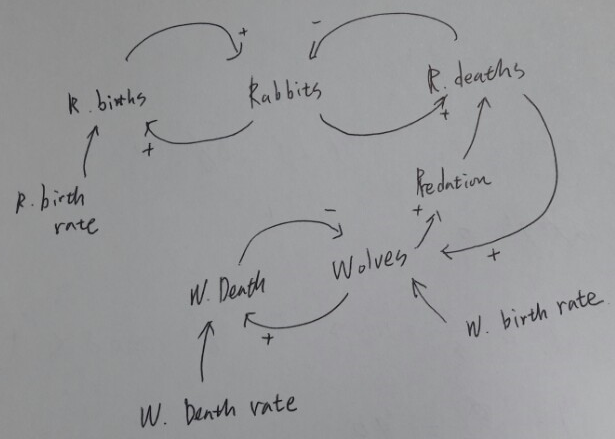
위의 식을 연습삼아 Causal loop diagram으로 표현해봤어요(고수님들 도움!)
미분 방정식이 이미 나와있으므로 역으로 이런 그림을 그리는건 별 의미가 없지만 연습삼아 그려봤습니다. 사실 Bxy 부분의 관계가 직관적으로 와닺지 않아서요.
아무튼 테스트하기 좋게 소스 코드 첨부 합니다.
import matplotlib.pyplot as plt
rabbit = [1001]
predator = [40]
birth = 0.2
death = 0.1
predation = birth/40.0
eat = death/1000
dt = 0.001
time = [0]
T = 100/dt
for i in range(int(T)):
new_rabbit = rabbit[i] + dt*(birth * rabbit[i] - predation * rabbit[i] * predator[i])
new_predator = predator[i] +dt* (eat * rabbit[i] * predator[i] - death * predator[i])
rabbit.append(new_rabbit)
predator.append(new_predator)
time.append(dt*i)
fig, ax1 = plt.subplots()
ax2 = ax1.twinx()
ax1.plot(time,rabbit,'g-')
ax2.plot(time,predator, 'r-')
ax1.set_xlabel('Time')
ax1.set_ylabel('Rabbits', color='g')
ax2.set_ylabel('Wolves', color='r')
plt.show()
위 코드는 파이썬으로 작성된 코드이고, @mauver 님 글(https://steemit.com/kr-dev/@mauver/01-python-setup) 참고하셔서 아나콘다 파이썬을 설치하면 별도의 라이브러리 추가 설치 없이 바로 테스트 할 수 있습니다.
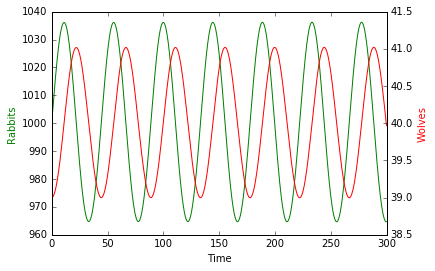
그림 5. 토끼와 늑대의 운명
그림 5를 보면 초반에 늑대가 없을 때 토끼(초록색 선)의 숫자는 늘어나지만, 먹이가 늘어나서 늑대의 인구도 늘어납니다. 하지만 늑대의 인구가 늘어난 만큼 마구마구 먹어대니 다시 토끼의 숫자가 줄어들면서 먹이가 부족해 늑대의 인구가 줄어드는 관계를 확인할 수 있습니다.
Predator-Prey의 두 식이 0이 되는 x와 y의 값을 찾으면 두 종 사이의 균형점을 찾을 수 있습니다. 사실 이것 외에 더 진지한 이야기들이 많지만 그건 저도 잘 몰라요. ㅎㅎㅎ 관심 있으신 분들은 위키피디아를 통해서 레퍼런스를 확인해봅시다.
5. 맺음
심시티 개발이라고 했지만, 제가 만든다면 심시티가 아니라 판타지 세상의 영지를 운영하는 게임을 기획할 것 같고 ... 위 Predator-Prey equations을 가지고 영지 주변의 목초지, 초식 동물, 몬스터의 관계를 구현하면 플레이어에게 고기를 얻고 마장을 만드는데 필요한 목초지를 늘리는 반동으로 몬스터의 숫자도 늘어나는 딜레마를 주도록 구현 할 것 같습니다.
지난 주 너무 바빠서 포스팅을 못했지만 틈틈히 고민하던걸 이렇게 하게 되서 개운하긴 합니다. 다음 포스팅은 차량 동역학, 시뮬레이션 레이싱 게임의 로직에 대해서 써볼까 합니다.
심시티 개발 1은 아직 몇가지 피드백 루프를 테스트하지 못해서 구현해보고 쓰겠습니다. 심시티 개발 2의 내용은 도시 교통 체증에 대한 이야기를 할거에요.
지금까지 쭉 써온 글을 보니 게임 개발이 아니라 기획... 도 아니고 설정 놀음을 하고 있다는 생각이 들어서 죄책감이 느껴집니다 ㅠ.ㅠ
Reference
[1] http://www.ebay.com/itm/THE-ORIGINAL-SIMCITY-SIM-CITY-1Clk-Macintosh-Mac-OSX-Install-/251506321233
[2] https://en.wikipedia.org/wiki/SimCity_(1989_video_game)#cite_note-7
[3] https://www.c64-wiki.com/wiki/Sim_City
[4] http://www.simulace.info/index.php/Causal_loop_diagram
인겜갤 토깽이 글 봤는데 지귀님 요기도 글을 쓰셨네요. 헤헤 잘 보고 갑니다아
지난 주 바빠서 방송 못갔는데, 요즘 너무 노는거 아닙니까?
ㅜ^ㅜ 혼자서 짐 테스트좀 하고 있습니다. 여러 곳 돌아다니면서.. 지금도 잠깐 쉬었다가 테스팅 하는데 뭐라고해야하나 처음 해보는 분야라서 ..
뭔가 엄청나네요..