SLC-S22W4//Linear and Quadratic equations equations

Greetings Steemit friends

Task 1: Explain difference between linear and quadratic equations. Provide examples of each type of system of equations and describe their general forms.

Last sessions we looked at linear and nonlinear systems of equations, and this week we are moving to linear and quadratic equations. They may have the same concepts but are not the same. This week I am looking at linear and quadratic equations.

Linear equations are equations whose highest power of the variable is 1 and represent a straight line when placed on a graph.

General form

ax + b = 0

Where:
a and b are constants
a is not equal to 0

Example

3x + 4 = 10 (Subtract 3 from both sides)
3x = 6 (Divide by 3)
x = 2

Quadratic Equations are equations whose highest power of the variable is 2 and represent a parabola when placed on a graph.

General Form

ax^2 + bx + c = 0

Where :
a, b, and c are constants
a is not equal to 0

Example

x^2−5x+6=0
x^2−5x + 6 = 0 (look for two numbers that we multiply to have 6 and when we add, we will have -5)
-2 * -3 = 6
-2 + -3 = -5

Rewrite Equations

(x − 2)(x − 3) = 0

Brake and solve each factor

x - 2 = 0
x = 2

x - 3 = 0
x = 3

Verify

Substitute x = 2 and x = 3

i)

x = 2
(2)^2 - 5(2) + 6 = 0
4 - 10 + 6 = 0
-6 + 6 = 0

ii)

x = 3
(3)^2 - 5(3) + 6 = 0
9 - 15 + 6 = 0
-6 + 6 = 0

This shows that both solutions are correct.

Task 2: Describe methods for solving quadratic equations and share the pros and cons of each method.

Quadratic equations can be solved by factoring, quadratic formulas, or graphing, which have been mentioned in the courses.

Solving Factoring: Here, you have to break down the equation into two binomial products. I solved the above quadratic using the factoring method.

Steps: Find two numbers that multiply to ac and add to b. Factor the equation set each equal to 0 and solve for x.

Pro: Simple and quick equations that can be factored
Cons: It can be very challenging to get the factors if the constants are large, and will only work if the quadratic can be factored.

Quadratic Formula:

x = (-b ± √(b^2 - 4ac)) / 2a

Where a, b, and c are coefficients from the quadratic equations.

Steps: Identify a, b, and c from the quadratic equation, apply to the quadratic formula, and simplify to get x.

Pros: It always works for both factorable and unfactorable equations
Cons: It can be very challenging when working with large numbers

Graphing :

y = ax^2 + bx + c

This method requires us to plot the quadratic function above and find the points of the x-axis intersection on the graph.

Step: Write the function y=ax^2+bx+c, plot the graph using a table of values, and identify the point of intersections.

Pros: Easy to get approximate solutions when plotting the parabola.
Cons: Need for graphing skills.

Task 3

i) Solve for linear equation 3x + 2 = 11 and show value of x?

ii) Solve for this quadratic equation x^2 + 2x - 6 = 0.

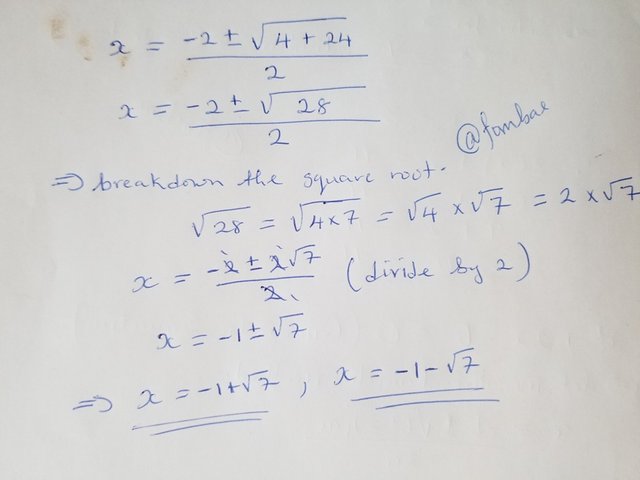
Task 4

• Scenario 1 is a linear equation that can be solved by finding the value of x. in this case.

x + 3 =15
Subtract 3 from both sides
x + 3 - 3 = 15 - 3
x = 12

That means Ali has $12 left after buying the pack of chips.

• Scenario 2 is to get the Maximum height of the ball, which is given by the equation.

h(t) = -5t^2 + 20t

Given that we have a coefficient of t^2 which is a negative value(-5), tell that height h(t) is a downward curve.

To get the time(t) at the maximum height, we used the formula.

t = -b/2a

h(t) = -5t^2 + 20t
-5t^2 + 20t - h(t) = 0

here a = -5, and b = 20

Calculate Time (t)

t = -20/2(-5)
t = -20/-10
t =20/10
t=2 seconds

We have the time(t=2 seconds) at maximum height, let go ahead to calculate the maximum height now. We have to substitute the time into the equation.

h(t) = -5t^2 + 20t

h(2) = -5(2)^2 + 20(2)
h(2) = -5(4) + 40
h(2) = -20 + 40
h(2) = 20 (divide both side by 2)
h = 20/2
h = 10

Finally

h = 10meters and in 2 seconds h(2) = 20 meters.

cc: @khursheedanwar

---

---

Cheers
Thanks for dropping by
@fombae