27-11-2024 - Education - Linear Algebra - Conics [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

[ENGLISH]
27-11-2024 - Education - Linear Algebra - Conics [EN]-[IT]
With this post I would like to provide some brief notions regarding the technical topic mentioned in the subject.
The context in which we operate is that of analytical geometry or linear algebra
(code notes: MOD-58)

Conics
Definition
Conics are algebraic curves of degree two. They are defined as the locus of points that satisfy a general equation of the form:

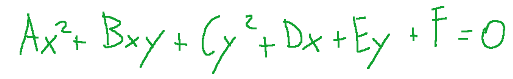
where A, B, C, D, E, F are real coefficients and

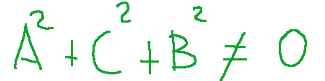
(this is to ensure that it is a second degree equation)

Types of conic sections
Depending on the values ​​of the coefficients A, B, C and the discriminant

Conic sections are classified into:
-Ellipse

Closed and oval shape where the particular case of the circumference A=C is included and B=0

-Parabola

An open curve with a single axis of symmetry, usually with a “U” shape

-Hyperbola

An open curve consisting of two distinct branches. Asymptotes define the direction of the branches.

Geometric definition
Conic sections can be defined geometrically as the locus of points that satisfy a property with respect to a pair of fixed elements in the plane.

Exercise
An exercise regarding conics can be the following.
Find the singular points of the degenerate conic of equation

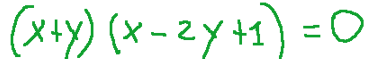
which is a pair of straight lines

Execution
Let's consider the homogeneous equation of the conic,

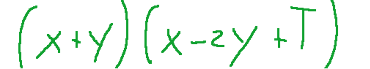
which can be rewritten as

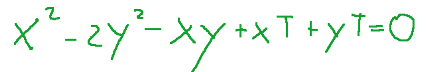
Let's calculate the three partial derivatives and set them equal to 0

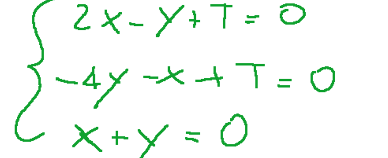
The system has the solutions

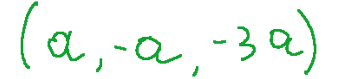
with

So the conic has a singular point, the following

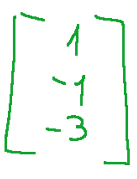
Conclusions
Conic sections are fundamental in geometry analytic and find applications in physics, engineering and astronomy.

Question
Have you ever studied conics in linear algebra or analytic geometry?

---

---

[ITALIAN]
27-11-2024 - Education - Algebra lineare - Coniche [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento tecnico citato in oggetto.
Il contesto in cui operiamo è quello della geometria analitica o algebra lineare
(code notes: MOD-58)

Coniche
Definizione
Le coniche sono delle curve algebriche di grado due. Esse sono definite come il luogo dei punti che soddisfano un'equazione generale della forma:

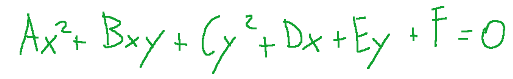
dove A,B, C, D, E, F sono coefficienti reali e

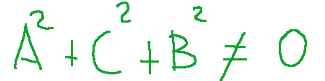
(questo per garantire che sia un’equazione di secondo grado)

Tipi di coniche
A seconda dei valori dei coefficienti A,B,C e del discriminante

le coniche si classificano in:
-Ellisse

Forma chiusa e ovale dove viene incluso il caso particolare della circonferenza A=C e B=0

-Parabola

Curva aperta con un unico asse di simmetria, solitamente con una forma a “U”

-Iperbole

Curva aperta costituita da due rami distinti. Gli asintoti definiscono la direzione dei rami.

Definizione geometrica
Le coniche possono essere definite geometricamente come il luogo dei punti che soddisfano una proprietà rispetto a una coppia di elementi fissi nel piano.

Esercizio
Un esercizio a riguardo delle coniche può essere il seguente.
Trovare i punti singolari della conica degenere di equazione

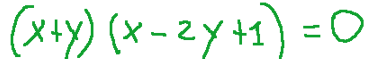
che è una coppia di rette

Svolgimento
Consideriamo l’equazione omogenea della conica,

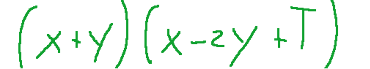
che può essere riscritta come

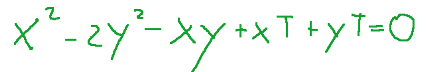
Calcoliamo le tre derivate parziali e poniamole uguali a 0

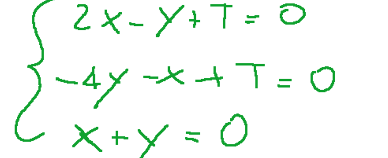
Il sistema ha le soluzioni

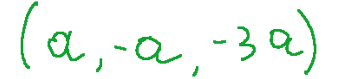
con

Quindi la conica ha un punto singolare, il seguente

Conclusioni
Le coniche sono fondamentali in geometria analitica e trovano applicazioni in fisica, ingegneria e astronomia.

Domanda
Avete mai studiato le coniche in algebra lineare o geometria analitica?

THE END