26-02-2025 - Education - Geometry - Distance between two points [EN]-[IT]
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
26-02-2025 - Education - Geometry - Distance between two points [EN]-[IT]
With this post I would like to provide some brief notions regarding the technical topic mentioned in the subject.
The context in which we operate is that of analytical geometry or linear algebra
(code notes: MOD-63)
Distance between two points
Today we try to see how to calculate the distance between two points in space.
Theory
In this case the theory is not very complex. To calculate the distance of two points in space you need to have the formula for the distance between two points at hand.
Let's imagine we have two points in space and define them as follows:
The formula to calculate the distance of the two points in space (described before in a generic way) is the following:
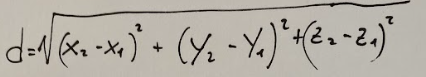
At this point we already have everything we need. So now if we had two points with all their x, y and z coordinates, taking the formula described before we would know how to calculate the distance between them.
Exercise
What is the distance between the two points t(5 -3 1) and t(2 1 -1) of space?
Our points are therefore
(5 -3 1) and (2 1 -1)
let's remember the formula we need to calculate the distance between two points in space (I'll report it below)
And now let's do the substitutions with our given points. Replace x1,x2,y1,y2,z1 and z2.
We will obtain what is described below:
We do the first step of the calculation by doing the sums/differences inside the brackets or members that will then be raised to the second.
Now let's calculate all the elements squared
Finally, by adding the three data obtained, we will have our result
Result final
Conclusions
We can say that the formula for calculating the distance between two points in three-dimensional space is an extension of the formula for the distance in the two-dimensional plane. Calculating the distance between two points in space is simple once you know and apply the relative calculation formula.
Question
Have you ever calculated the distance between two points in space? Have you ever done exercises at school like the one I showed here?

[ITALIAN]
26-02-2025 - Education - Geometria - Distanza tra due punti [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento tecnico citato in oggetto.
Il contesto in cui operiamo è quello della geometria analitica o algebra lineare
(code notes: MOD-63)
Distanza tra due punti
Oggi proviamo a vedere come si fa a calcolare la distanza tra due punti nello spazio.
Teoria
In questo caso la teoria non è molto complessa. Per calcolare la distanza di due punti nello spazio bisogna avere sottomano la formula della distanza tra due punti.
Immaginiamo di avere due punti nello spazio e definiamoli come segue:
La formula per calcolare la distanza dei due punti nello spazio (descritta prima in maniera generica) è la seguente:
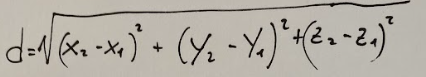
A questo punto abbiamo già tutto quello che ci serve. Quindi ora se avessimo due punti con tutte le loro coordinate x, y e z, prendendola la formula descritta prima sapremmo calcolare la distanza che c'è tra loro.
Esercizio
Quanto vale la distanza tra i due punti t(5 -3 1) e t(2 1 -1) dello spazio?
I nostri punti sono quindi
(5 -3 1) e (2 1 -1)
ricordiamo la formula che ci serve per calcolare la distanza tra due punti nello spazio (la riporto qui sotto)
Ed ora andiamo a compiere le sostituzioni con i nostri punti dati. Sostituire x1,x2,y1,y2,z1 e z2.
Otterremo quanto qui di seguito è descritto:
Facciamo il primo passaggio del calcolo andando a fare le somme/differenze all'interno delle parentesi o dei membri che verranno poi elevati alla seconda.
Ora andiamo a calcolare tutte gli elementi elevati al quadrato
Infine andando a sommare i tre dati ottenuti avremo il nostro risultato
Risultato finale
Conclusioni
Possiamo dire che la formula per calcolare la distanza tra due punti nello spazio tridimensionale è un'estensione della formula della distanza nel piano bidimensionale. Il calcolo della distanza tra due punti nello spazio è semplice una volta che si conosce e che si applica la relativa formula di calcolo.
Domanda
Avete mai calcolato la distanza tra due punti nello spazio? Avete mai svolto degli esercizi a scuola tipo quello che ho mostrato qui?
THE END

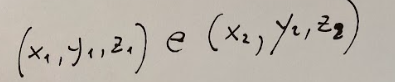
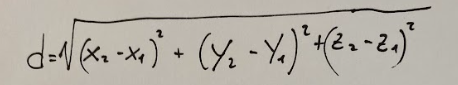
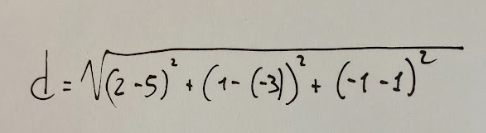
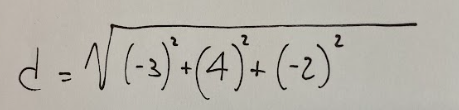
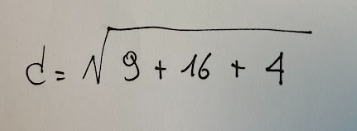
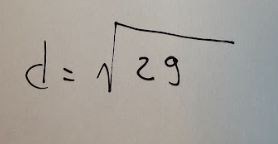
I have done them both at work and at university, I find it easy and I like it.
I also think these exercises are not extremely complicated. Once you know a single shape and have all six data you can get to the result
sempre molto affascinanti le tue mini lezioni di geometria spaziale !
vorrei provare a chiederti un approfondimento piu tecnico su un campo che per te potrebbe essere facile da spiegare
Mi stai sopravvalutando… sono cose che tiro fuori da vecchi appunti scolastici o dalle note scritte durante corsi di formazione
non ho mai calcolato la distanza ipotetica da 2 punti ma mi hai dato un idea interessante da provare
Una volta compresa la formula il calcolo della distanza non è impossibile da effettuare
che cosa intrigante queste formule e la matematica in tutte le sue sfaccettature
Sono d’accordo con te, la matematica, la geometria, la chimica e la fisica sono tutte materie intriganti. Io non capisco perché da giovane i professori mi facevano odiare tutte queste materie che oggi adoro.
Upvoted! Thank you for supporting witness @jswit.