14-06-2025 - Exercise - linear programming problem [EN]-[IT]
Cover background image generated with AI, software used: copilot microsoft
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
14-06-2025 - Exercise - linear programming problem [EN]-[IT]
Image generated with AI, Microsoft Copilot
With this post I would like to provide some brief notions about the topic mentioned in the subject by doing some exercises.
The context in which we operate is that of Operations Research
(code notes: MOD+14)
Linear Programming Problem
Exercise 01
Let's consider the following Linear Programming problem
Let's try to solve the problem by applying Phase 2 of the Simplex method starting from the basic feasible solution determined in Phase 1
Initial considerations
Minimize the function objective
Below are the constraints.
The steps that will have to be performed are the following:
-Determine the initial basic solution (provided by Phase 1)
-Build the Simplex table with initial basis
-Calculate the reduced coefficients to determine the direction of improvement
-Perform the pivot to update the basis
-Repeat until the optimization is achieved
Building the initial table
Starting from the second equation we can immediately obtain:
So we will have that the solution of initial basis is as follows:
Checking for optimality
In the case of minimization, the solution is optimal if all the reduced coefficients are >= 0
In this case we have:
-3 < 0
-2 < 0
But we must be careful, in the table, x1 and x2 are already in the basis, so there are no non-basic variables to introduce. From this we can deduce that the solution is already optimal.
We can therefore conclude that:
-The initial basic solution is admissible and optimal
-It is not necessary to pivot or perform subsequent iterations
-The objective function has a minimum value:
Optimal solution found
Optimal value of the objective function:
Optimal solution.
This is the solution that minimizes the objective function respecting the given constraints.
Below is an extension of the calculation process
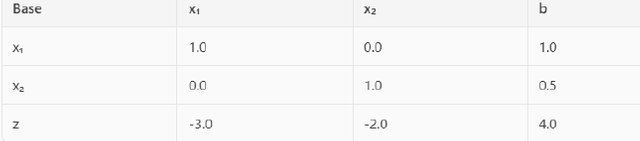
Initial table of the Simplex method
Below is the initial table of the Simplex method (Phase 2) for the given problem:
The initial basic variables are x1 and x2. Column b represents the current solution x1 = 1.0, x2 = 0.5
The last row of the table shows the reduced coefficients of the objective function.
We can make the following consideration.
Since the latter are all negative, the solution is optimal for a minimization problem.
Conclusions
A linear programming exercise similar to the one just performed can be used to determine the optimal solution of a problem with two variables and two constraints, starting from a basic feasible solution. This type of exercise helps to understand the fundamentals of optimization and to develop analytical skills.
Question
I must admit that in the school environment 40 years ago the school subject of Operations Research was not very widespread.
Have you ever heard of the school subject called Operations Research before?

[ITALIAN]
14-06-2025 - Esercizio - problema di programmazione lineare [EN]-[IT]
Immagine generata con IA, Microsoft Copilot
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento citato in oggetto svolgendo degli esercizi.
Il contesto in cui operiamo è quello della Ricerca operativa
(code notes: MOD+14)
problema di programmazione lineare
Esercizio 01
Consideriamo il problema di Programmazione Lineare seguente
Proviamo a risolvere il problema applicando la Fase 2 del metodo del Simplesso a partire dalla soluzione di base ammissibile determinata nella Fase 1
Considerazioni iniziali
Minimizzare la funzione obiettivo
Qui di seguito sono riportati i vincoli.
I passaggi che si dovranno eseguire saranno i seguenti:
-Determinare la soluzione di base iniziale (fornita dalla Fase 1)
-Costruire la tabella del Simplesso con base iniziale
-Calcolare i coefficienti ridotti per determinare la direzione di miglioramento
-Effettuare il pivot per aggiornare la base
-Ripetere fino al raggiungimento dell’ottimizzazione
Costruzione della tabella iniziale
Partendo dalla seconda equazione possiamo ottenere subito:
Quindi avremo che la soluzione di base iniziale è quanto segue:
Verifica dell’ottimalità
Nel caso di minimizzazione, la soluzione è ottima se tutti i coefficienti ridotti sono >= a 0
In questo caso abbiamo:
-3 < 0
-2 < 0
Dobbiamo però fare attenzione, nella tabella, x1 e x2 sono già in base, quindi non ci sono variabili non di base da introdurre. Da questo possiamo dedurre che la soluzione è già ottima.
Possiamo quindi arrivare alla conclusione che:
-La soluzione di base iniziale è ammissibile e ottima
-Non è necessario fare pivot o iterazioni successive
-La funzione obiettivo ha valore minimo:
Soluzione ottimale trovata
Valore ottimo della funzione obiettivo:
Soluzione ottima.
Questa è la soluzione che minimizza la funzione obiettivo rispettando i vincoli dati.
Qui di seguito un ampliamento del processo di calcolo
Tabella iniziale del metodo del Simplesso
Qui di seguito la tabella iniziale del metodo del Simplesso (Fase 2) per il problema dato:
Le variabili di base iniziali sono x1 e x2. La colonna b rappresenta la soluzione corrente x1 = 1.0, x2 = 0.5
L’ultima riga della tabella mostra i coefficienti ridotti della funzione obiettivo.
Possiamo fare la seguente considerazione.
Poiché questi ultimi sono tutti negativi, la soluzione è ottima per un problema di minimizzazione.
Conclusioni
Un esercizio di programmazione lineare simile a quello appena eseguito, può servire per determinare la soluzione ottima di un problema con due variabili e due vincoli, partendo da una soluzione di base ammissibile. Questa tipologia di esercizi aiuta a comprendere i fondamenti dell’ottimizzazione e a sviluppare capacità analitiche.
Domanda
Devo ammettere che in ambito scolastico 40 anni fa la materia scolastica di Ricerca Operativa non era molto diffusa.
Avete mai sentito parlare prima d'ora della materia scolastica chiamata Ricerca Operativa?
THE END


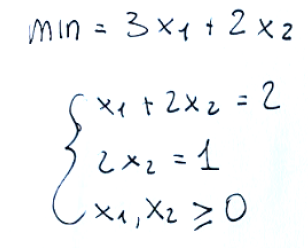
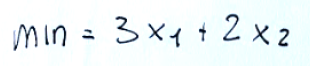
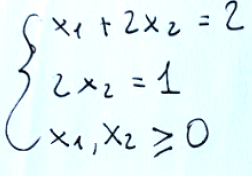
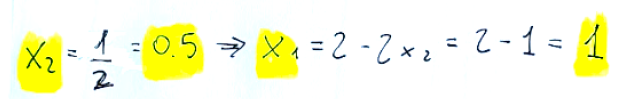
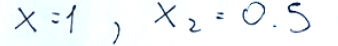
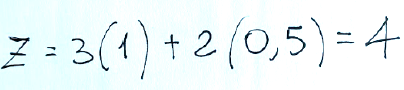
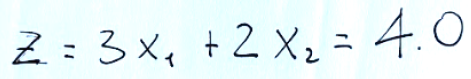
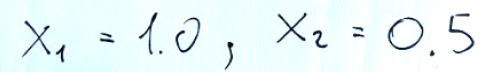
Voglio dirti qualcosa di diverso dalla domanda, quando vedo questa lavagna, mi ricordo quando mia madre mi ha insegnato ad aggiungere e sottrarre, usava il gesso per la lavagna, mi ricordo che è andata via la corrente, arriva alle 9 pm di sera o qualcosa del genere, e mia madre si alza molto stanca di fare i lavori domestici e il suo lavoro di insegnante, mi dice, dai, dobbiamo finire quello che abbiamo iniziato, mia madre è meravigliosa, le voglio molto bene, scusa per i miei ricordi nostalgici condivisi con te
Grazie per aver condiviso con me questo bellissimo ricordo di tua madre... posso quasi immaginare tutto il bene che ti vuole e che ti ha voluto, ma non credo di poterlo comprendere a pieno in quanto deve essere infinitamente grande..
Purtroppo no, ma avendo frequentato un istituto magistrale non c'è da stupirsi (ma dubito pure che questa materia fosse presente nel curriculum del liceo classico). Già era impensabile riportare all'insegnameno alle elementari gli argomenti delle materie tecniche e scientifiche allora presenti e avanzate pure per noi, quindi figuriamoci Ricerca Operativa. Possibilmente presente nel curriculum da liceo scientifico (ma non ne sono troppo sicura, dato che la mia scuola eleborava il suo curriculum proprio sulla falsariga dello scientifico), meglio ancora in un istituto tecnico commerciale (che ai miei tempi c'era però soltanto a Cuneo, quanto a Piemonte) o magari a ragioneria.
Ciao POU, infatti ho fatto una piccola ricerca e due chiacchere con qualche mio collega laureato. Ricerca Operativa è una materia che oggi è legata soprattutto all'ambiante tecnico universitario. Esempio, ingegneria gestione, informatica, matematica, economia e management
Ah, ecco perchè non mi suonava affatto. In un istituto tecnico è comunque comprensibile la presenza di Ricerca Operativa. Nei licei e nelle care vecchie scuole abilitanti non troppo tecniche no.
sinceramente non sapevo proprio dell esistenza di questa materia , ma devo ammettere che spiegata cosi ha un senso pratico se inserisci le variabili per poter ottenere un risultato
Grazie per aver lasciato un commento. La programmazione lineare aiuta a trasformare i problemi in equazioni matematiche o sistemi matematici, in modo da poter dare delle soluzioni ammissibili. In questo articolo il problema era piuttosto semplice, peró mi fa piacere che tu abbia compreso il senso della programmazione lineare
Very useful information, thanks for sharing.
Thank you for leaving a comment. Linear programming became popular in the 1950s/1960s but was developed primarily by George Dantzig, an American mathematician and computer scientist, in the 1940s.
😊😊👍
This post has been upvoted by @italygame witness curation trail
If you like our work and want to support us, please consider to approve our witness
Come and visit Italy Community
Upvoted! Thank you for supporting witness @jswit.