04-09-2025 - Exercise - Maximum Number of Choices [EN]-[IT]
Cover background image generated with AI, software used: copilot microsoft
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
04-09-2025 - Exercise - Maximum Number of Choices [EN]-[IT]
Image generated with AI, Microsoft Copilot
With this post, I would like to provide some brief insights into the topic mentioned above by completing some exercises.
The context in which we operate is that of Operations Research
(lesson/article code: QE_09)
Maximum Number of Choices
First, let's identify the concept of linear programming, which is a very important branch of operations research. Linear programming is a mathematical technique for making optimal decisions. This mathematical technique is used when the objective and constraints are linear.
Stating that the objective and constraints are linear means that all the mathematical relationships describing the problem are expressed by linear functions of the decision variables.
Essentially, the mathematical formula that appears in the objective function contains no powers.
In other words, we can say that the objective and constraints are linear when the problem can be described with lines and planes in the space of variables.
Now let's get to the point...
In linear programming, when we talk about maximum number of choices, we usually mean the maximum number of possible basic solutions.
** 3 constraints and 4 variables**
Given a linear programming problem in standard form with 3 constraints and 4 variables, the maximum number of basic solutions is 4.
Why is this?
In a linear programming problem in standard form with m constraints and n variables, a basic solution is obtained by choosing m basic variables from the n available, while the other n-m are set to zero.
Based on this concept, we can calculate the maximum number of choices with the following formula:
Essentially, we need to count how many combinations of 4 objects taken at random can exist.
The step-by-step calculation is as follows:
Recall the formula above and that:
m=3 (constraints)
n=4 (variables)
4! will have this value.
3! will have the following value
1! will have the following value:
At this point, we apply the substitution of values in the formula noted above.
Result
The maximum number of basic solutions is 4, as I wrote at the beginning of the exercise, and the choices are precisely these four triplets below. reported:
Conclusions
In a linear programming problem, the maximum number of choices is given by the combination of variables and constraints. For example: if we have 4 variables and 2 constraints, we will have 4 maximum basic solutions; if we have 4 variables and 2 constraints, we will have 6 maximum basic solutions. In linear programming, the maximum number of choices is studied because it is a theoretical upper bound; this is useful in combinatorial analysis to understand the complexity of a problem.
Question
Have you ever tried to do linear programming exercises? Have you ever tried to understand the maximum number of basic solutions a linear programming exercise can have?

[ITALIAN]
04-09-2025 - Esercizio - Numero massimo di scelte [EN]-[IT]
Immagine generata con IA, Microsoft Copilot
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento citato in oggetto svolgendo degli esercizi.
Il contesto in cui operiamo è quello della Ricerca Operativa
(codice lezione/articolo: QE_09)
Numero massimo di scelte
Innanzitutto identifichiamo il concetto di programmazione lineare, che è un ramo molto importante della ricerca operativa. La programmazione lineare è una tecnica matematica per prendere decisioni ottimali. Questa tecnica matematica si usa quando l'obiettivo e i vincoli sono lineari.
Affermare che l’obiettivo e i vincoli sono lineari significa che tutte le relazioni matematiche che descrivono il problema sono espresse da funzioni lineari delle variabili decisionali.
Sostanzialmente nella formula matematica che appare nella funzione obiettivo non ci sono potenze.
Con parole diverse possiamo dire che obiettivo e vincoli sono lineari quando il problema può essere descritto con rette e piani nello spazio delle variabili.
Arriviamo ora al dunque...
In programmazione lineare quando parliamo di numero massimo di scelte di solito ci riferiamo al numero massimo di soluzioni di base possibili.
** 3 vincoli e 4 variabili**
Dato un problema di programmazione lineare in forma standard con 3 vincoli e 4 variabili il massimo numero di soluzioni di base è 4.
Perché questo?
In un problema di programmazione lineare in forma standard con m vincoli e n variabili, una soluzione di base si ottiene scegliendo m variabili di base tra le n disponibili, le altre n-m si pongono a zero.
In base a questo concetto possiamo calcolare il numero massimo di scelte con la seguente formula:
Sostanzialmente dobbiamo contare quante combinazioni di 4 oggetti presi a 3 possono esserci.
Il calcolo passo passo è il seguente
ricordiamo la formula scritta sopra e che:
m=3 (vincoli)
n=4 (variabili)
4! avrà questo valore
3! avrà il seguente valore
1! avrà il seguente valore
A questo punto applichiamo la sostituzione dei valori nella formula segnata prima
Risultato
Il massimo numero di soluzioni di base è 4 come avevo scritto all'inizio dell'esercizio e le scelte sono proprio queste quattro terne qui di seguito riportate:
Conclusioni
In un problema di programmazione lineare il numero massimo di scelte è dato dalla combinazione tra variabili e vincoli. Esempio: se abbiamo 4 variabili e tra vincoli avremo 4 soluzioni di base massime, se abbiamo 4 variabili e 2 vincoli avremo 6soluzioni di base massime. In programmazione lineare viene studiato il numero massimo di scelte perché è un limite superiore teorico, questo è utile in analisi combinatoria per capire la complessità di un problema.
Domanda
Avete mai provato a fare degli esercizi di programmazione lineare? Avete mai provato a capire il massimo di soluzioni base che può avere un esercizio di programmazione lineare?
THE END


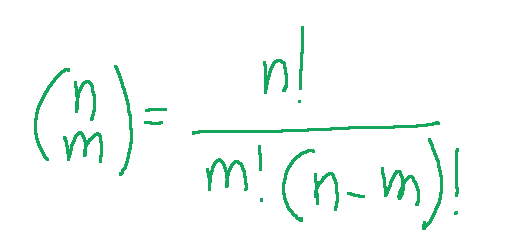
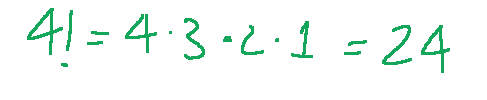
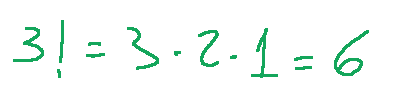
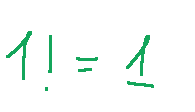
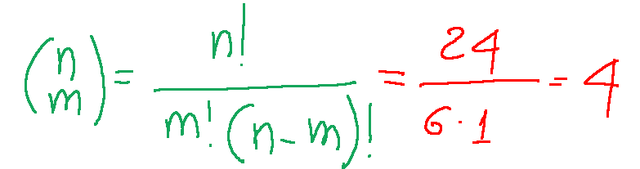
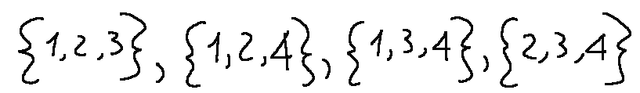
Nice information.
0.00 SBD,
0.26 STEEM,
0.26 SP
Thanks for stopping by. This is a linear programming exercise. Essentially, it's a sort of pre-processing to understand how many solutions a problem can have. These exercises are performed primarily in logistics to understand how many routes a means of transportation can take and then choose the most convenient one.
Very good and very useful, we can try to practice it.
Very useful information, thank you for sharing.😊
0.00 SBD,
0.25 STEEM,
0.25 SP
Thank you for leaving a comment. With this article, I wanted to highlight what can be a preliminary analysis of a linear programming problem. Linear programming is a mathematical technique used to optimize an objective (called an objective function) under linear constraints. The objective could be, for example, maximizing profit or minimizing cost.
Now I know, thank you very much for the explanation. Very useful.
Upvoted! Thank you for supporting witness @jswit.
0.00 SBD,
0.25 STEEM,
0.25 SP
This post has been upvoted by @italygame witness curation trail
If you like our work and want to support us, please consider to approve our witness
Come and visit Italy Community
0.00 SBD,
0.24 STEEM,
0.24 SP